两条几何规律在圆边界磁场中的应用

柯 尧

(九江市第一中学 江西 九江 332000

带电粒子在磁场中的运动是高考物理的重要考点，以考查粒子在有界磁场中的运动为主，它有效地考查了学生利用几何知识处理物理问题的能力．磁场边界类型主要包括直线边界、矩形边界、圆边界、抛物线边界等，每种边界都有相应的规律，这些规律是解决问题的前提，甚至是突破口．圆边界磁场，由于对称性，更有特殊规律可寻．

规律1：同一平面内，两相交圆关于连心线对称．

图1 例1题图

解析：粒子在有界磁场中运动，解题思路可总结为简单的9个字“画轨迹、定圆心、求半径”．本题作为该卷物理部分的压轴题，难度较大，其原因是考生在作出轨迹圆后找不到合适的几何关系求半径．对于这类圆边界问题，如果能够利用规律“同一平面内，两相交圆关于连心线对称”来求解，将会十分简便，甚至不必作出粒子的运动轨迹．

如图2所示，过圆边界的圆心作出入射方向的平行线与边界交于e和f，过入射点a作入射方向的垂线段ga，且g为轨迹圆圆心，ga交线段ef于c点．

图2 作辅助线

由题意知，出射方向与入射方向垂直，磁偏角为90°，根据对称性有：∠Oga=45°,在Rt△Oca中

在Rt△gOc中

gc=Occot45°

因此轨迹半径

其他解答略．

点评：此解法利用了一个很基本的几何规律，避免了画轨迹和找复杂的几何关系．利用上面的几何规律可进一步得到结论：带电粒子射入圆磁场时，入射点处的轨迹半径所在直线与对称轴的交点为轨迹圆圆心，且夹角总等于粒子飞出磁场过程中磁偏角的一半．这条物理规律可以处理粒子从圆上某点沿任何方向入射的大部分问题．

如图3所示，正粒子从P点射入垂直纸面向外的匀强磁场，P点到与入射方向平行的直径距离为d，粒子射出磁场时偏转角为θ． 由上面物理规律不难求得粒子轨迹半径为

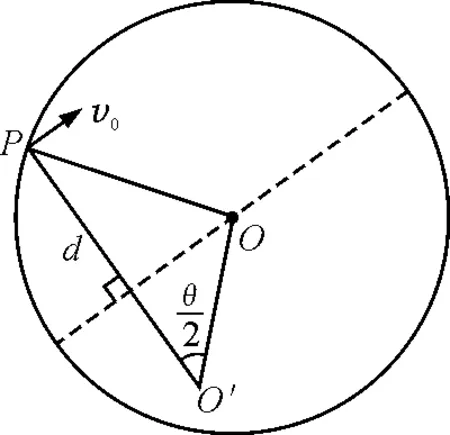
图3 举例

此方法极大地简化了相关题的求解，甚至解题时直接利用公式即可，比如公式可以直接解答2013年全国新课标Ⅰ卷选择题第18题．上面结论的特殊情况为d=0，入射点轨迹半径所在直线与边界圆相切，由对称性知粒子出射点轨迹半径所在直线亦与边界圆相切，即粒子对着圆心入射，出射方向必过圆心，如2013年全国新课标Ⅱ卷选择题第17题可用此规律．

规律2：同一平面内，半径相等的两相交圆的交点与两圆圆心构成菱形．

【例2】(2009年高考浙江卷第25题)如图4所示，x轴正方向水平向右，y轴正方向竖直向上．在xOy平面内与y轴平行的匀强电场，在半径为R的圆内还有与xOy平面垂直的匀强磁场．在圆的左边放置一带电微粒发射装置，它沿x轴正方向发射出一束具有相同质量m，电荷量q(q>0)和初速度v的带电微粒．发射时，这束带电微粒分布在0

(1)从A点射出的带电微粒平行于x轴从C点进入有磁场区域，并从坐标原点O沿y轴负方向离开，求电场强度和磁感应强度的大小与方向．

(2)请指出这束带电微粒与x轴相交的区域，并说明理由．

图4 例2题图

解析：第(1)问解答略．

第(2)问，由上问知：mg=qE，轨迹半径r=R，根据几何规律“同一平面内，半径相等的两相交圆的交点及两圆圆心构成菱形”，可从边界入射点中任取一点P进行分析说明，如图5所示.设Q为出射点,O1，O2分别为磁场边界圆和轨迹圆圆心，顺次连接4点，显然四边形四边相等，知四边形PQO1O2为菱形，PO2∥O1Q，由于入射方向水平，PO2必为竖直方向，O1Q也为竖直方向，且长度为R，Q必与坐标原点O重合,P为任意点，所以这束带电微粒均与x轴交于原点O．

图5 第(2)问的分析用图

点评：粒子轨迹半径与圆边界半径相等是粒子在圆边界磁场中运动的重要特征条件，相关问题都可通过作菱形求解．利用特殊的4点构成菱形可以得到结论：大量轨迹半径等于磁场边界半径的粒子若平行入射至圆形磁场区，出射时必汇聚于边界的某一点(磁聚焦)；若从圆边界上某点沿边界平面向圆内任意方向发射，必平行出射．

对于几乎所有的带电粒子在从圆边界入、出射的问题，都可尝试用本文的规律，半径相等就采用第二条规律，其他问题基本上利用第一条规律都可以得到解决．从上面两道高考压轴题可看出，一些需要利用复杂几何关系或者其他数学方法才能求解的粒子运动问题，如果能结合恰当的规律，将会使题目求解变得简单明了．作为物理教师，有必要去总结和发现这样的有利于解题的规律．