矢量喷管三维数值模拟
(中国石化集团新星石油有限责任公司 北京 100083)
拉瓦喷管的主要作用是将亚音速气流转变为超音速的气流。如今这一技术已经在多个领域内都具有广泛的运用。在冶金行业内[1],吹氧装置中的氧枪喷头便是利用拉瓦喷管进行金属熔池中的供氧,并参与传质传热和化学反应促使钢种的冶炼和生产。在能源运输行业内[2],拉瓦喷管的引进使得近海油田中天然气的运输设备更加的紧凑可靠。拉瓦喷管也具有很强的雾化性能,可以用来形成理想粒径和均匀的雾云分布[3]。其中,运用最为广泛的是航天航空领域,很多飞行器的发动机采用拉瓦喷管使尾气加速到很高速度以获取更大的推力,从而加强飞行动力。
随着科技的发展以及时代的需要,张丽等人[4]提出了飞行器姿态控制,即有效地实现飞行器姿态稳定和姿态机动之间的切换,实现飞行器的俯仰、偏航和翻滚。这些性能的实现尤其对于战斗机进一步发展至关重要。战斗机的高机动性和敏捷性非常重要,通常要求具有良好的大攻角气动特性,但是攻角较大时,全机的流态,特别是升力面处于完全分离状态。尽管优良的气动布局或许可以保证飞机不至于发生偏离和翻滚,但是其操作效率却大幅下降,大大地降低了飞机的机敏性。而矢量喷管可以通过推力矢量的控制,即用推力矢量代替或补偿常规有装置的气动力进行飞行控制。这样的技术对于飞机性能的提升具有很大的作用。推力矢量控制技术不仅可以使飞行中的飞机获得更好的超机敏性,而且推力矢量和推力反作用的共同作用下可以有效地降低飞机起飞与着陆距离。此外,推力矢量的控制下飞机飞行的最小速度可以有效的减小。因此,推力矢量控制是实现飞行器姿态控制,提高战斗机机动性和敏捷性的有效措施。
矢量喷管可以形成推力的控制,拉瓦喷管作为推进系统的重要组成部分,其内部的流动特性对于推力的生成具有很大的影响。拉瓦喷管通常地设计与生产依赖于风洞试验,但是这种方法周期长,耗资大,而且存在流动温度压力等条件的限制,这使得目前计算流体力学方法成为了拉瓦喷管气动性能分析的常规手段。关于矢量喷管的研究最早始于70年代的美国,他们主要针对于二元推力矢量喷管进行了相关的研究,实现了喷管上下扩散调节片在俯仰方向偏转20度。之后随着计算流体力学的发展,更多的学者针对拉瓦喷管技术进行了数值模拟研究。王平[5,6]等人结合一维等熵管流理论对于拉瓦喷管的典型工作流场进行了二维数值模拟,其结果很好地证明了数值模拟的可靠性。朱伶枫等人[7]针对于马赫数为1.7的拉瓦喷管进行了多种不同湍流模型的二维数值模拟,模拟结果对比表明标准k-ω模型和标准的k-ε模型与试验测量值相差较大,其他模型模拟结果均差别不大,其中SSTk-ε模型的模拟结果与实验测量数据的吻合度最高。随着矢量喷管技术的发展,有关矢量喷管内部流场性能的研究也得到了许多学者的关注。王如根[8]等人利用过对喷管偏转后流场变化进行了二维数值模拟计算,结果表明偏转结构对于喷管内部的流场分布影响不大。这样的结果说明矢量喷管在实现推力矢量控制的前提下并不会造成额外的流动恶化。
前人的研究中大都采用二维数值模拟计算,而且均未给出不同偏转角度下矢量喷管所形成的推力大小。因此,本文中采用三维数值模拟不同偏转角矢量喷管的内部流场并计算不同偏转角矢量喷管的推力情况。而且,在此之前本文首先对于拉瓦喷管典型工作流场进行三维模拟以确定该种模拟计算结果的稳定性。
一、物理模型
本文的研究对象为拉瓦喷管,目的是通过数值模拟实现简单拉瓦喷管之中的各种工况,以及进行矢量喷管内部流动状态的分析。用以本次模拟计算的为三维几何模型,简单拉瓦喷管的三维几何模型由选定进出口截面半径与喉部截面半径之后,以直线相连接通过共同中心轴构成的旋转结构。该缩放喷管模型的进出口截面积与喉部截面积之比为4:1,收缩段与扩散段长度保持相同。矢量拉瓦喷管相比之下喉部之后的扩散段部分则出现了不同角度的偏转,但是仍然保证进出口截面积与喉部截面积之比为4:1,收缩段与扩散段长度一致。本文主要进行简单拉瓦喷管中各种流动工况的数值模拟实现和理论研究结果对比,以及针对偏转角度分别为5°、10°、15°的三种矢量拉瓦喷管进行其内部流动状态的分析。如图1中所示即为本文中所探究的所有几何模型XY平面内沿轴线对称部分的二维几何结构以及相关尺寸设置。
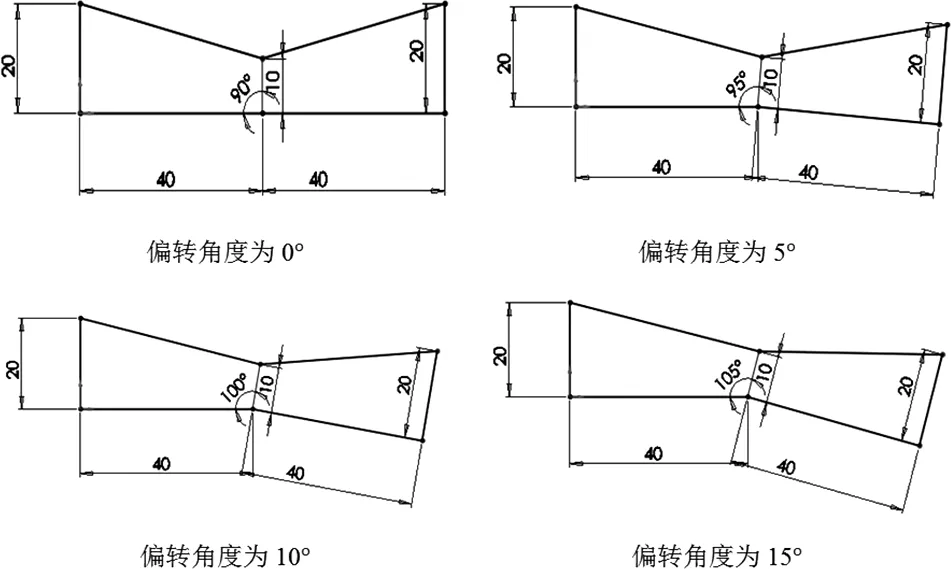
图1 不同偏转角矢量喷管的几何模型
二、管内流动性能理论分析
(一)拉瓦喷管的流动状态分析
拉瓦喷管中由于气流流速快,而拉瓦喷管的几何规模一般较小,因此气流在拉瓦喷管中所停留的时间非常短暂。由于拉瓦喷管之中气流停留时间的短暂导致气流与外界来不及进行热交换或不能充分进行热交换,因此可以近似将此过程看作为绝热过程。在拉瓦喷管中气流流动过程中气流的各参数变化较为连续,而且粘性影响小,流道又短从而使得摩擦累积效应很小,因此可以近视认为此过程为可逆过程。由以上两条绝热过程以及可逆过程的合理近似假设可以得知拉瓦喷管中的气流流动可看作为等熵流动,而且流动参数的变化仅由流道面积的改变造成。流体工质可以近似假定为理想气体,因而拉瓦喷管之中的流动最终可以简化为绝热等熵的一维流动。
绝热等熵一维流动之中给定一个马赫数会有唯一的面积比与之对应,但是给定一个面积比则会有两个马赫数相对应,其中一个为亚音速一个为超音速。当流速等于当地音速,即流动的马赫数为1时,被称之为临界状态,所对应的参数称之为临界参数。因此,当喉部达到临界状态时质量流量达到最大,此时,喉部下游的扩张段内会出现两种连续的等熵流动,一种对应于扩张段内均为亚音速流动,另一种对应于扩张段内均为超音速流动。计算公式如下:
(1)
上式中流体工质假定为理想气体,故其绝热指数k=1.4,则可以解得Ma1=0.1465;Ma2=2.9402。绝热等熵一维流动之中压力具有如下关系:
(2)
若假定拉瓦喷管内进口压力为标准大气压,通过改变背压来实现各种工况的模拟。则可解得亚音速解为pc=99817.3234 Pa;超音速解为pj=3018.07。
由正激波关系式:
(3)
可以解得pf=29935.941 Pa。
拉瓦喷管之中的流动状态通常可以用三个压强(pc、pf、pj)将其大致分为四个区段:
第一区段:p>pc,即进出口压差小于1507.6766 Pa,此时整个拉瓦喷管之中为亚音速流动,出口压强即为背压。当背压为临界压力pc时,喉部达到音速,继续降低也不会对收缩段内的流动状态造成影响及通过喷管的质量流量不会再发生变化。
第二区段:pc>p>pf,即进出口压差大于1507.6766 Pa,小于71389.059 Pa,此时扩张段某处会出现正激波,喉部至正激波之前为超音速流动。而正激波之后即为亚音速流动。出口压强即为背压,而且当背压为pf时,正激波将会移动至喷管的出口位置。
第三区段:pf>p>pj,即进出口压差大于71389.059 Pa,小于98306.931 Pa,此时整个拉瓦喷管扩张段内均为超音速流动,气流流出管外之后其压力经过斜激波后升高至背压。当背压为pj时,激波消失,出口截面压强即为背压。
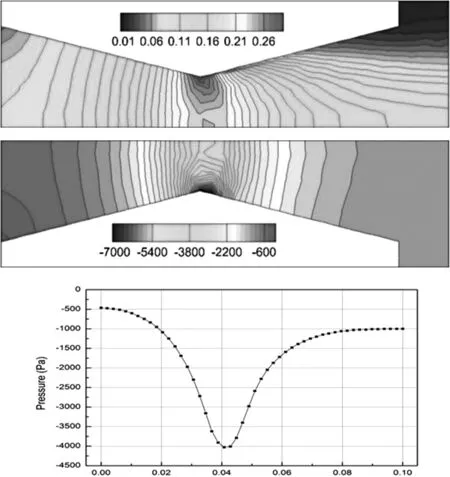
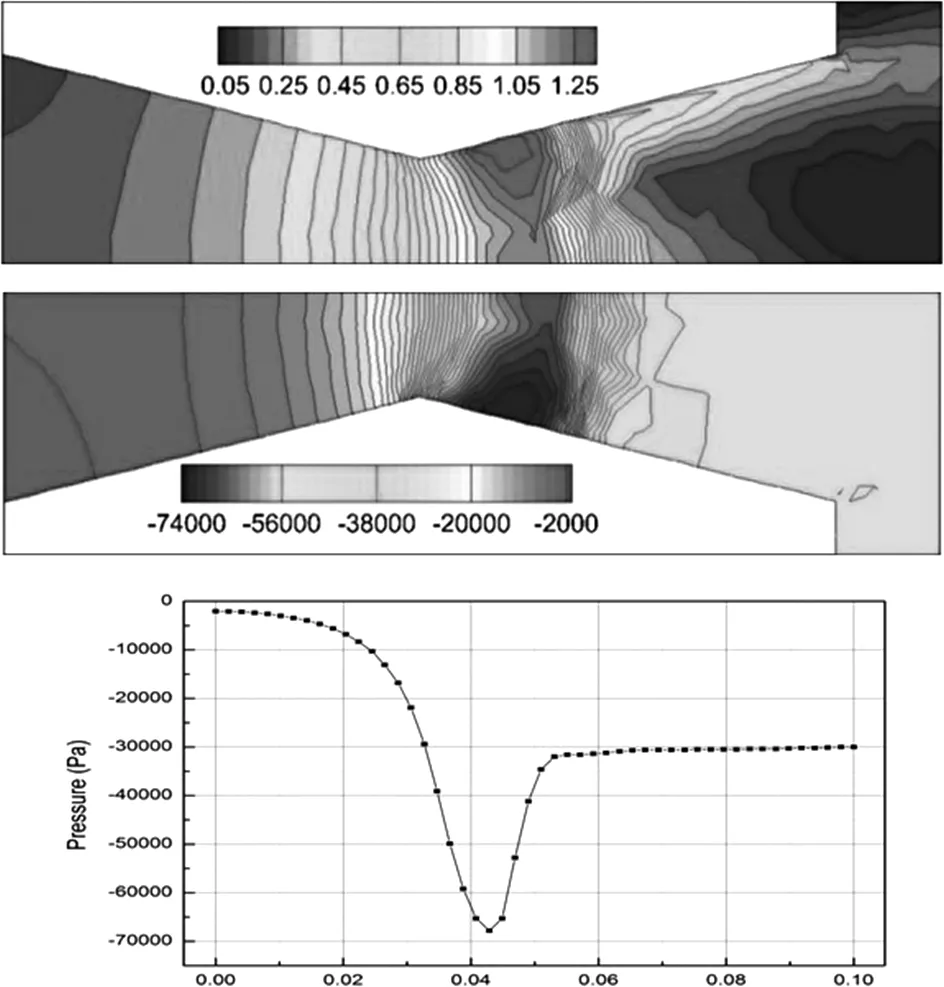
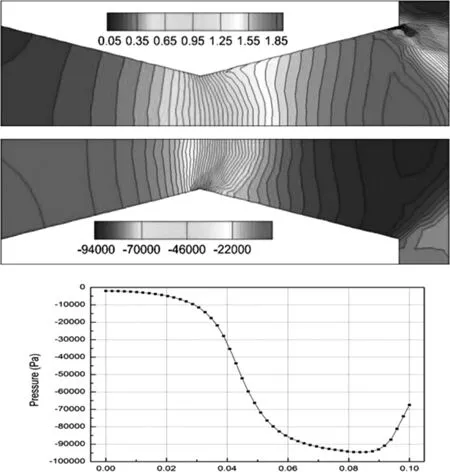
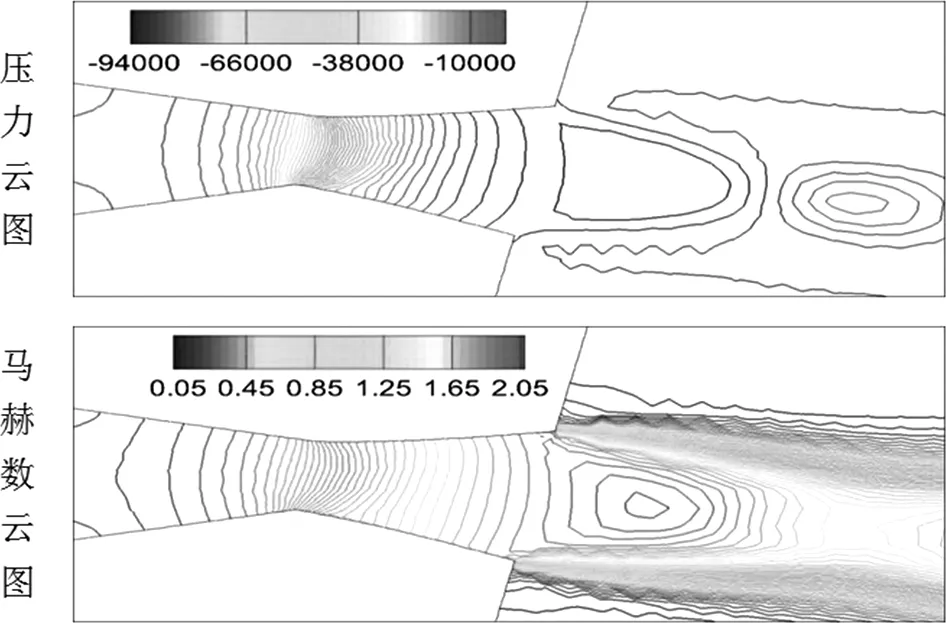
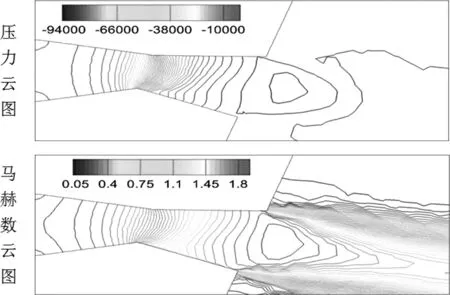
第四区段:p (二)矢量喷管性能参数计算 推力矢量控制是通过改变矢量喷管的几何偏转角,从而使出口气流方向发生改变以得到大小和方向不同的推力来满足飞机机动性能的要求。模拟计算矢量喷管中为定常流动,则由于气流方向偏转而引起各个方向的推力可以由动量方程求得。定常流动下的动量方程为: Fx=Δm·U-(pin·Ainx-pout·Aoutx) Fy=Δm·V+pout·Aouty (4) Fz=Δm·W 其中Fx、Fy、Fz分别表示X、Y、Z方向的轴向推力,俯仰推力以及偏航推力;Δm为出口截面上的质量流量,U、V、W分别为出口截面在X、Y、Z方向的速度。 (一)控制方程 可压缩流动的强守恒型N-S方程为: (5) 其中: (6) ρ为密度,P为压力,u,v,w为X,Y,Z方向的速度分量,e为单位体积内能,总能量E,压力P以及内能e可以表示为: P=ρ(k-1)e (7) e=CvT 上式中的k为气体比热比,对于理想气体取值为1.4,T为气体温度,Cv为定容比热。 其中: (8) 上式中: (9) (10) (11) (二)数值方法及边界条件 本文研究所采用的流动工质为理想气体,数值计算采用商用计算流体力学软件ANSYS CFX来求解三维拉瓦喷管以及矢量喷管的内部流动性能。该模型的网格采用四面体网格生成技术,湍流模型采用SST模型。假定参考压力为标准大气压,保证进口压力为标准大气压不变,即通过调整背压来实现工况的改变,壁面设置为绝热条件。 (一)拉瓦喷管模拟结果与理论结果对比 根据理论计算结果分别进行各区段内不同工况的计算,并将模拟计算结果同理论流动规律进行相互验证,借此证实模拟计算的正确性以及可靠性。通过理论计算可得:当拉瓦喷管进出口压差小于1507.6766 Pa时,流动状态处于第一区段,由此选定第一区段的模拟工况为△P=1000Pa;当进出口压差大于1507.6766Pa,小于71389.059Pa,流动处于第二区段,由此选定第二区段的模拟工况为△P=30000Pa;当进出口压差大于71389.059Pa,小于98306.931Pa,流动状态处于第三区段,由此选定第三区段的模拟工况为△P=80000Pa;当进出口压差大于98306.931Pa,流动状态处于第四区段,但是实际模拟计算时发现与理论计算结果之间并不相符。当△P=90000Pa时,模拟结果显示已经达到了第四区段所描述的流态。 图2 △P=1000Pa时,马赫数和压力云图以及沿X轴的压力分布 图2中给出了处于第一区段内流动位于X轴上方的马赫数云图和位于X轴下方的压力云图,以及X轴上压力变化曲线。由图中的马赫数云图可以看出,在该工况下拉瓦喷管内流体均为亚音速,此工况所对应的压力取值也正好位于理论计算的第一区段压力范围之内。综合马赫数云图、压力云图以及沿X轴的压力分布图可以看出从拉瓦喷管进口到喉部的收缩段内流体流速不断的增加,压力不断降低,在喉部位置时速度值达到最大,其压力值达到最小,之后的扩张段内流体流速开始降低,其压力也相应回升,在出口处达到背压并维持不变。以上所述模拟结果所呈现的现象与拉瓦喷管中流体理论运动规律基本相符。另外,根据对于压力云图和马赫数云图的观察可以发现在拉瓦喷管外壁面转折处由于几何因素的突然改变导致压力和马赫数都发生了较为显著的变化,形成了局部的高速区域以及对应的低压区域。 图3 △P=30000Pa时,马赫数和压力云图以及沿X轴的压力分布 图3中给出了处于第二区段内流动位于X轴上方的马赫数云图和位于X轴下方的压力云图,以及X轴上压力变化曲线。第二区段内流动理论规律表明在拉瓦喷管喉部可以达到音速,而且扩张段内将出现正激波。流体在正激波之前均为超音速流动,正激波之后则变为亚音速流动。由上图中的马赫数云图可以发现其喉部位置速度确实达到音速,而且在扩张段内也实现了由超音速到亚音速的快速转变。由与之对应位置处的压力云图可以发现,此处的压力变化非常剧烈,通过X轴的压力分布曲线可以更加直观地发现当速度达到最大之后,压力由最小值迅速地升高至背压并保持不变,该现象与可以迅速增压使得流动从超音速变为亚音速的正激波相对应。以上的模拟结果分析同理论规律对比结果相符,则可证明模拟结果的可靠性。 图4 △P=80000Pa时,马赫数和压力云图以及沿X轴的压力分布 图4中给出了处于第三区段内流动位于X轴上方的马赫数云图和位于X轴下方的压力云图,以及X轴上压力变化曲线。该区段内的理论上流动在整个拉瓦喷管之中持续加速膨胀,压力也相应持续降低直到喷管出口之后经过斜激波导致压力迅速升高,达到背压后保持不变。根据图4中的马赫数云图、压力云图以及此处X轴上压力变化曲线可以发现流体在整个拉瓦喷管内压力以及马赫数变化都非常均匀,直到喷管出口位置处变化变得剧烈,该现象在X轴上压力的变化曲线处得到了更加直接的证明。 图5 △P=90000Pa时,马赫数和压力云图以及沿X轴的压力分布 图5中给出了处于第四区段内流动位于X轴上方的马赫数云图和位于X轴下方的压力云图,以及X轴上压力变化曲线。由图5中的马赫数云图以及压力云图可以看出在该种工况下流体流速在拉瓦喷管之中不断地增加,其压力值则不断地减小。图中沿X轴上压力分布变化曲线更加直观的表示出了拉瓦喷管之中流动从进口到出口之间的压力值变化规律。根据以上的分析可得该工况所对应的就是理论中第四区域的流动状态。 对比不同区段内沿X轴方向压力的分布规律可知,在第一,第二,第三区段内,位于拉瓦喷管喉部之前的收缩段中的压力均呈现出相同下降趋势,即先下降平缓,之后下降速度快速增大,在喉部之后的扩张段内,压力又会出现回升,从而导致逆压出现。而在第四区段内的压力下降趋势却与之不同,其压力下降速度开始时非常迅速,之后则慢慢变缓,而且在整个运动过程之中压力不断地下降,期间无逆压生成。根据两种不同的压降趋势可以看出第四区段内的流动会更加的稳定,不易出现涡结构等不利于流动的流动特征。 综上所述,模拟计算结果与理论研究基本规律基本上相互吻合,只是由于理论计算时的各种假设条件,使得理论计算的较高压差部分的流动状态分布范围与模拟结果不太一致。但是,理论体系中的相关流动发展规律与流体运动现象在模拟计算结果中都有相应的体现,这些可以相互验证的结果表明了模拟计算结果是可靠的。 (二)矢量喷管性能分析 根据矢量喷管性能的探究与实验,目前矢量喷管主要被期望运用于战斗机之上,为战斗机的高机动性能以及敏捷性作出有效的提高。由于战斗机不仅需要灵活的可控性,而且对于动力的要求也是更加苛刻,因此通常要求缩放喷管内尾气加速到很高的速度以达到相应的推力要求。因此,针对△P=90000Pa,对于5°、10°、15°不同偏转角的三种矢量喷管进行模拟计算,进而分析不同偏转角的矢量喷管形成的推力差异和不同偏转角下矢量喷管之中的马赫数以及压力的变化情况。 表1 矢量喷管推力计算结果 根据表中测量所得的数据结果可知,由于拉瓦喷管喉部位置已经达到声速,而且喉部面积均相同,因此各种不同偏转角的矢量喷管内的流量都相同。在X轴方向上和Z轴方向上,喷管出口速度随着偏转角的增加而逐渐减小,然而,在Y轴方向的速度值却随着偏转角的增加变得更大。由于矢量喷管的偏转角都比较小,因此大部分的气流沿着X轴方向流出,即所产生的推力也大部分位于X轴方向。在Y轴和Z轴方向上速度大小相比于X轴上的速度值相对较小。相应的,位于Y轴和Z轴方向上推力相对于X轴方向上的推力也比较小。但是随着偏转角的增加以及拉瓦喷管几何结构的改变会得到满足要求的各个方向上的矢量推力。 偏转角为5° 偏转角为10° 偏转角为15° 对比图6中不同偏转角下的压力云图可以发现尽管偏转角不同,但是压力在拉瓦喷管之内都是持续不断地降低,而且下降的速度也相差不大,比较均匀。这表明,随着偏转角的增加,拉瓦喷管内部流动状态并未出现显著地变化,即并未增加流动阻力,涡结构等额外的耗散。这使得大偏转角的矢量喷管的使用少了许多的顾忌。根据图6中马赫数云图的观察可以发现,拉瓦喷管内部的马赫数云图结构几乎完全相同,只是在喷管出口之后的区域内当偏转角为10°时,马赫数的最高值略大于偏转角为5°和15°。 本文首先对于拉瓦喷管中的经典工况的特征压力进行了理论假设计算并进行了各区段流动状态的理论分析。然后,根据理论计算进行相关参数的选取,并采用三维数值模拟方法进行了相应区段内经典工况的模拟计算。理论分析结论与数值模拟计算结果之间进行了相互对比论证,结果证实了三维数值模拟方法的可靠性。在这种三维数值模拟方法可靠性得到验证之后,本文又针对不同偏转角(0°、5°、10°、15°)矢量喷管进行了三维数值模拟,并对比了其内部流场分布差异以及进行了各偏转角矢量喷管理想压差条件下矢量推力大小的计算。通过本文的研究,最终可以得出以下结论: (1)针对拉瓦喷管进行的三维数值模拟结果与理论分析结论基本一致,对应不同区段内流体的流动状态基本相符; (2)当矢量喷管偏转角由5°到15°增大时,所形成的俯仰推力不断增大。由于偏转角度较小,其他方向上的矢量推力变化并不明显。 (3)矢量喷管内部压强以及马赫数分布并不会因为偏转角的差异而出现较大的变化,即偏转角的变化不会对矢量喷管内部流场造成很大的不利影响。 【参考文献】 [1]袁张福,潘贻芳.炼钢氧枪技术[M].北京:冶金工业出版社,2007. [2]Jassim,Esam,M.Abedinzadegan Abdi,and Yuri Muzychka.“Computational fluid dynamics study for flow of natural gas through high-pressure supersonic nozzles:Part 1.Real gas effects and shockwave.” Petroleum Science and Technology 2008,26.15 1757-1772. [3]杨超,陈波,姜万录,高殿荣,金光俊.基于拉瓦尔效应的超音速喷嘴雾化性能分析与试验.Transactions of the Chinese Society of Agricultural Engineering,2016,32(19). [4]耀保,张丽,贾萍,傅俊勇.飞行器姿态控制用拉瓦尔喷管的流场分析.液压气动与密封,2013,(1). [5]王平,刘学山,乔立民.轴对称拉瓦尔喷管流场分析.飞机设计,2013,33(2),23-26. [6]王平,李昌平,陈柏松.基于CFD数值模拟的拉瓦尔喷管流场分析.航空计算技术,2012,42(4),60-62. [7]朱伶枫,张延玲,朱荣,赵飞,田冬东.超音速射流流场湍流模型适应性研究.太原理工大学学报,2015,46(1),49-54. [8]王如根,赵瑞贤,李全通.空军工程学院飞机推进系统实验室 99学术会议三、拉瓦喷管的CFD计算方法
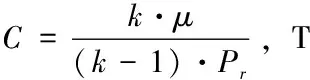
四、计算结果分析



五、结论
——运动的诗篇

