应用SPSS统计分析软件分析供应因素对房地产价格的影响

(重庆交通大学 重庆 400074)

一、问题提出及其背景

通过翻阅《重庆市统计年鉴》，发现自重庆市直辖以来，房地产价格逐年发生变化，而竣工房屋价值、本年土地购置费用、房地产开发投资总额各种供应因素也存在变化，于是，大胆猜测供应因素对房地产价格存在影响。为了证实这一猜想，本文将利用统计分析软件来统计分析收集到的数据。

本文数据源于《重庆市统计年鉴》，数据可信度高。

二、数据分析

(一)数据文件的建立

将上述数据输入SPPS中，输入如图1所示：

图1

图2

图3

图4

(二)相关分析

1.散点图。房屋价值与商品房销售价格的散点图如图2所示；本年土地购置费用与商品房销售价格的散点图如图3所示；房地产开发投资总额与商品房销售价格的散点图如图4所示；以上三个散点图表明，竣工房屋价值、本年土地购置费用、房地产开发投资总额三种供求因素与商品房销售价格都有一定的线性相关关系，其中竣工房屋价值与商品房销售价格的线性关系最强。

2.相关系数。虽然散点图能够直观展现变量之间的统计关系，但并不精确。相关系数以数值的方式能精确地反映了两个变量间线性相关的强弱程度。

商品房销售价格与竣工房屋价值的简单相关系数为0.983，与本年土地购置费用的简单相关系数为0.962，与房地产开发投资总额的简单相关系数为0.961，它们的相关系数检验的概率p值都近似为0。

(三)偏相关分析

偏相关分析所采用的工具是偏相关系数。

首先，将竣工房屋价值设置为控制变量，研究商品房销售价格与本年土地购置费用和房地产开发投资总额的净相关的程度强弱，结果如表1所示。由表1得到的结论与相关分析的结论差距甚远。

然后，将本年土地购置费用设置为控制变量，研究商品房销售价格与竣工房屋价值和房地产开发投资总额的净相关的程度强弱，结果如表2所示。

表2和表3均说明竣工房屋价值对商品房销售价格的线性影响较强。

表1

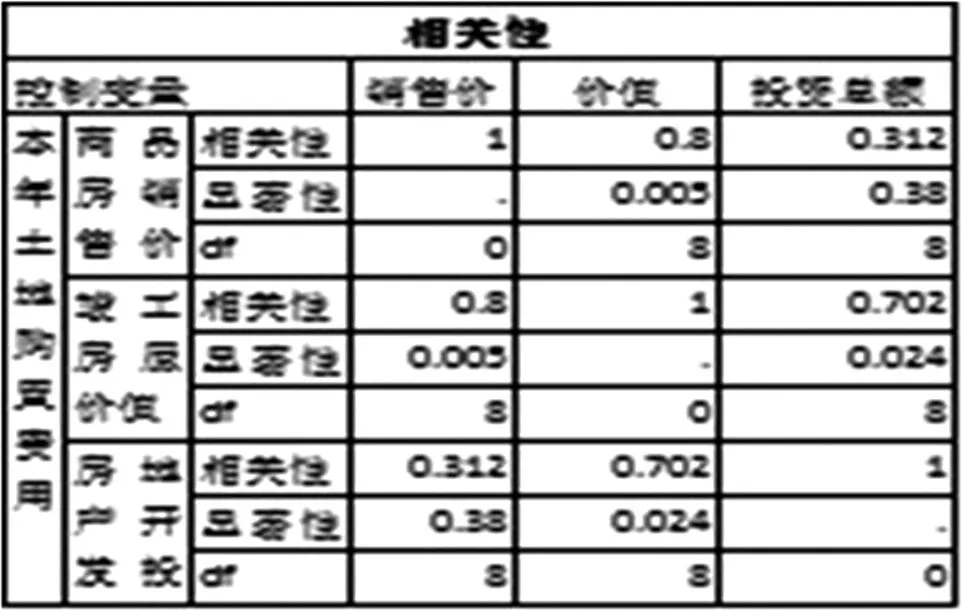
表2

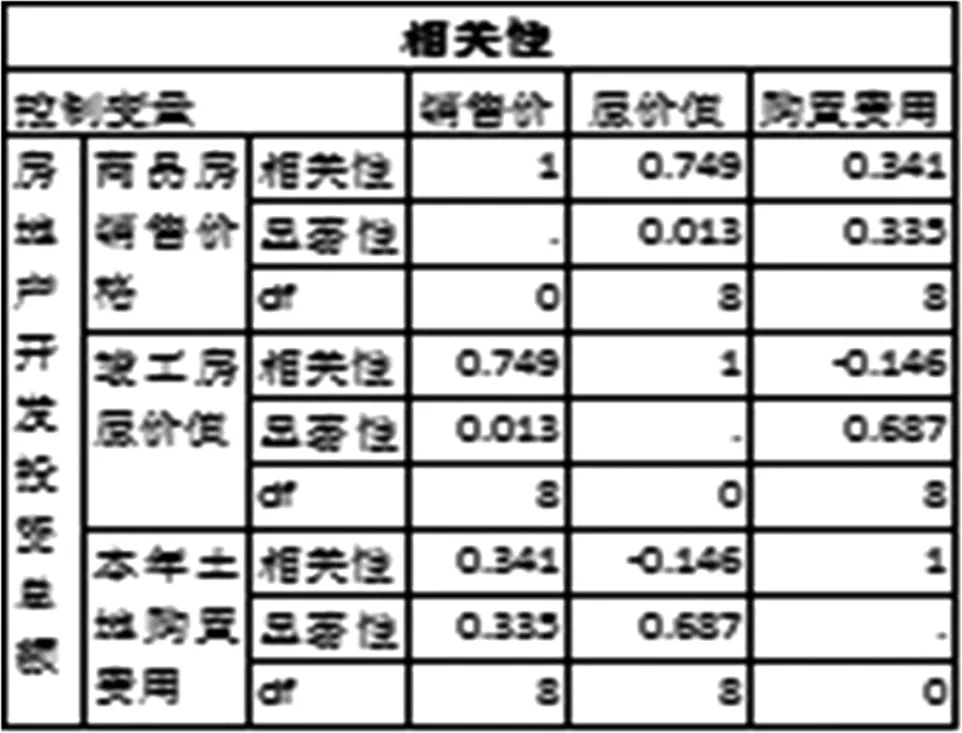
表3

(四)回归分析

1.本文选重庆市商品房销售价格为被解释变量Y，竣工房屋价值X1、本年土地购置费用X2和房地产开发投资总额X3为解释变量。(2)确定回归模型：通过观察散点图确定被解释变量与解释变量之间存在线性关系，拟建立多元线性回归模型。(3)建立回归方程：y=β0+β1x1+β2x2+β3x3+ε(4)对回归方程进行各种检验。采用向后筛选策略建立模型，选择逐步回归策略完成解释变量的选择。分析结果如下表4所示。

依据表5可进行拟合优度检验。判定系数(0.983)较接近于1，因此认为拟合优度较高。由于回归方程显著性检验的概率P值小于显著性水平α，因此被解释变量与解释变量之间的线性关系显著，建立模型是恰当的。

由表6可知，回归方程为：y=1386.616+3.505x1。变量的回归系数显著性t检验的概率P值小于显著性水平α，因此，认为回归系数与0有显著性差异，解释变量与被解释变量的线性关系是显著的。表7展示了变量剔除方程的过程。在模型中，保留本年土地购置费用和房地产开发投资总额的情况下，它们的标准化回归系数将分别为0.27和0.03，但回归系数的检验不显著(概率P值均大于0.05)。

表4

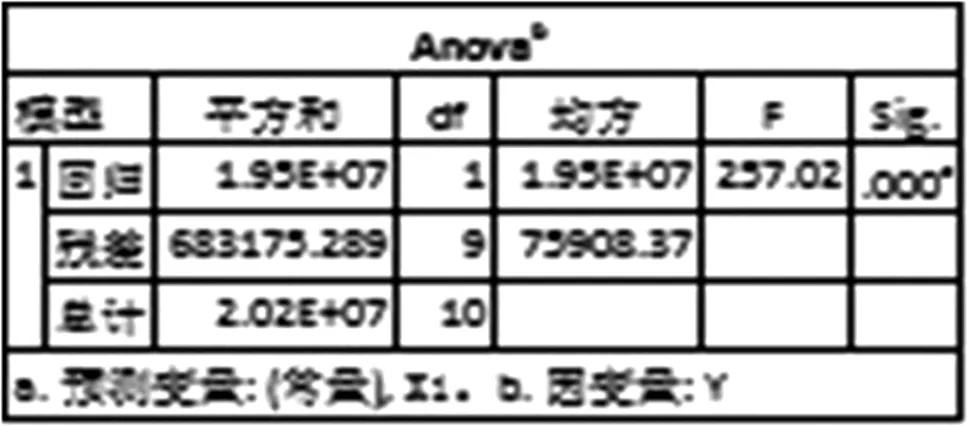
表5

表6

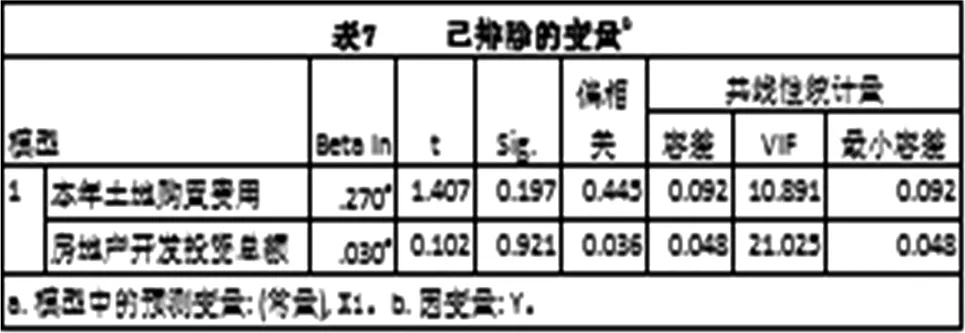
表7

(五)残差检验

利用回归分析中的绘图功能，得到数据的残差统计量及标准化残差图，如表8和图5所示。

由表8中数据，标准化残差与标准正态分布不存在显著差异，可以认为残差满足了线性模型的前提。由图5可知，数据点围绕基准线存在一定的规律性，但是，根据残差统计数据表(即表8)的结果表明残差满足了线性模型的前提要求。

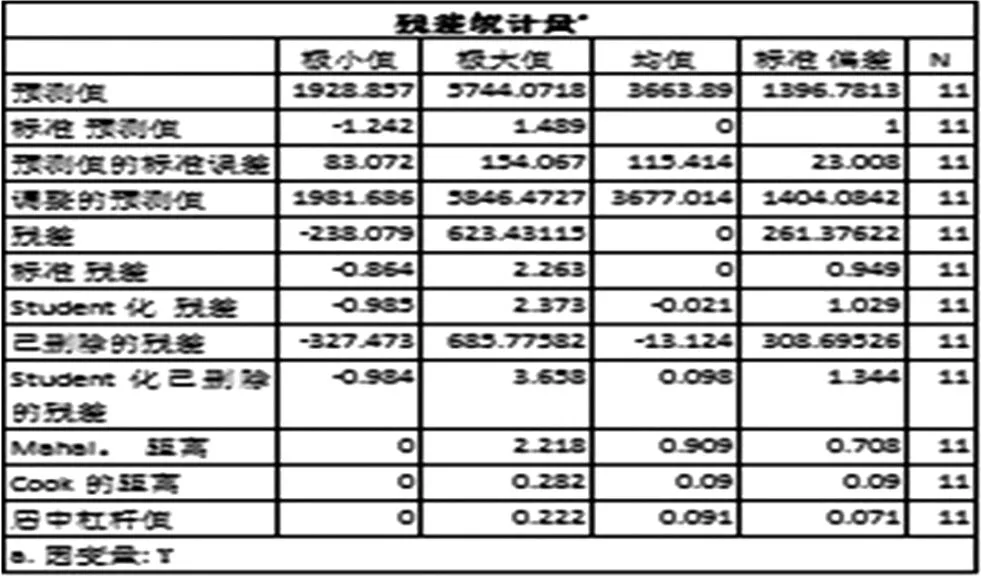
表8

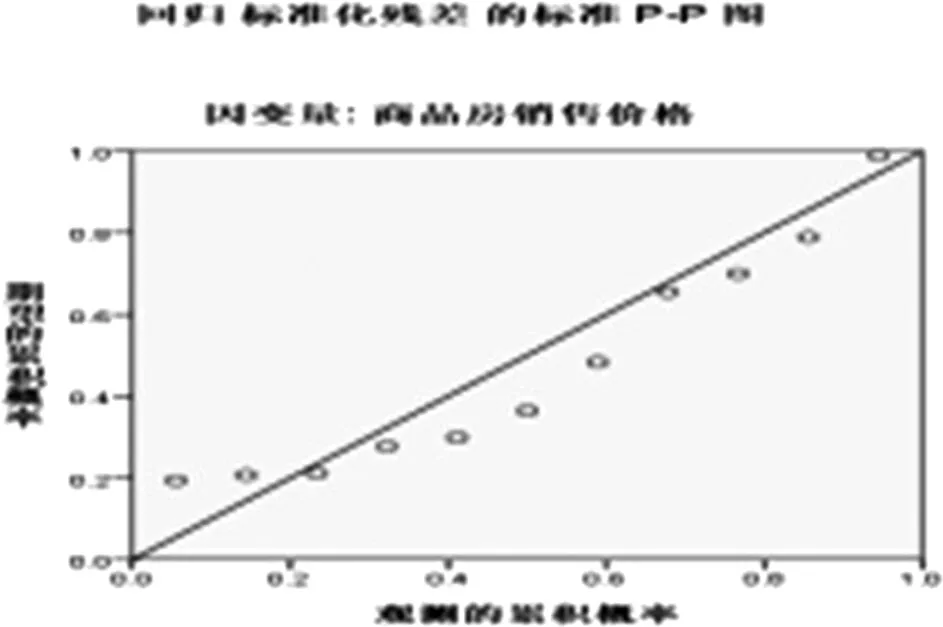
图5

三、结论

通过应用SPSS统计分析软件分析重庆的竣工房屋价值对商品房销售价格的影响，得到竣工房屋价值x和商品房销售价格y的线性回归方程：

y=1386.616+3.505x

从对于2004—2014年相关数据的回归分析中，我们可以得到以下结论：

(1)本年土地购置费用和房地产开发投资总额与人均商品房销售价格显著相关，但没有显著影响商品房销售价格，不能构成影响商品房销售价格的解释变量。故我们剔除了该解释变量，初步估计是由于本年土地购置费用和房地产开发投资总额的不确定性过大，抑制了它更进一步发挥对商品房销售价格的影响作用。拟合出仅含一个自变量的回归模型。

(2)竣工房屋价值对商品房销售价格具有较大的影响，随着这个解释变量的增加，商品房销售价格显著提升，构成影响商品房销售价格的关键因素。