浮板配流泵用球面型连通套摩擦副的一种设计方法

权云晴 李冀鹏 刘会祥 王宇浩 朱 熠



浮板配流泵用球面型连通套摩擦副的一种设计方法

权云晴 李冀鹏 刘会祥 王宇浩 朱 熠

（北京精密机电控制设备研究所，北京 100076）

针对浮板配流结构，采用剩余压紧力法进行球面型连通套环形摩擦副设计。对球面型连通套进行受力分析，给出了工程可用的压紧系数计算公式，并利用Fluent软件的流场仿真结果确定了球面型连通套环形摩擦副的压紧系数范围。

浮板配流结构；剩余压紧力法；环形摩擦副；流场

1 引言

伺服泵是机电静压系统的关键元件之一，其液压性能的好坏一定程度上取决于泵的配流机构工作性能的优劣。轴向柱塞泵的“浮动体”一般为泵缸体或配流盘。泵缸体为浮动体时，配流盘是固定的，有时存在泵缸体因受力不平衡而发生倾覆的情况。泵缸体倾覆将导致配流盘不均匀磨损并增大泄漏[1]。在浮板配流结构中，浮板配流盘始终保持浮动，当泵缸体发生微小倾斜时，浮板配流盘在贴紧泵缸体的同时也发生微小倾斜，可有效减少泵缸体倾覆对配流盘的磨损。

球面型连通套的球面凹台与固定盘形成环形摩擦副。在球面型连通套环形摩擦副设计中，若压紧系数过小，则会增大伺服泵的泄漏量；若压紧系数过大，则会影响球面型连通套的灵活性，最终导致浮板配流盘跟随性差。

针对浮板配流结构，以球面型连通套为研究对象，采用剩余压紧力法进行球面型连通套环形摩擦副设计，考虑多种受力因素，得到了工程可用的压紧系数计算公式。为得到压紧系数计算公式中的液膜承载力，利用Fluent软件对环形摩擦副内液膜进行三维流场数值模拟，根据数值模拟结果确定了球面型连通套环形摩擦副的压紧系数范围。

2 浮板配流结构

浮板配流结构如图1所示。泵缸体2刚性地固定在伺服泵转轴1上，由转轴1带动旋转。球头螺钉5对浮板配流盘3进行定位，使浮板配流盘3与固定盘4保持一定的浮动间隙，但允许浮板配流盘3轻微转动。在浮板配流盘3吸油、压油侧各均匀配置2组球面型连通套以产生足够的压紧力。球面型连通套6内放推力弹簧7。在伺服泵未工作或起动瞬时，推力弹簧7一方面以较小的压紧力将球面型连通套6压向固定盘4，另一方面使浮板配流盘3贴紧泵缸体2。在伺服泵正常工作后，作用在球面型连通套6右侧端面上的液压力使之与固定盘4保持贴紧；作用在球面型连通套孔内的高压油对浮板配流盘3的液压力稍大于柱塞腔中的高压油对柱塞腔底部的液压力，也就是说，浮板配流盘3受到的向右的液压力略大于泵缸体2对浮板配流盘3向左的轴向力，因此浮板配流盘3将与泵缸体2保持贴紧。

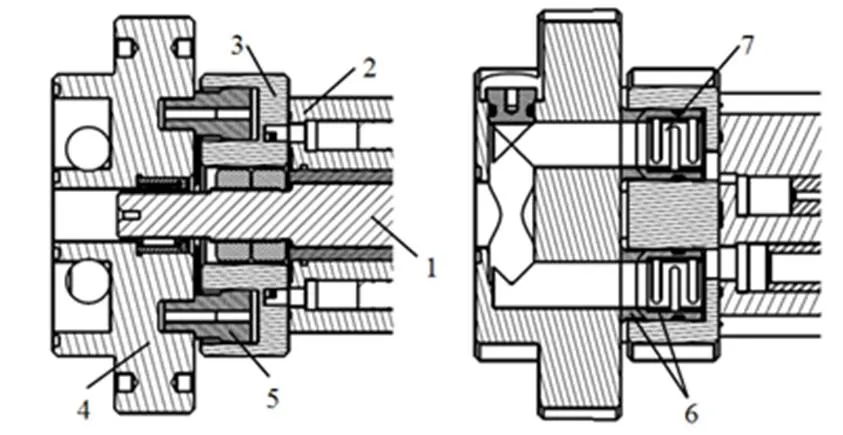
1—转轴 2—泵缸体 3—浮板配流盘 4—固定盘 5—球头螺钉6—球面型连通套 7—推力弹簧

3 球面型连通套结构

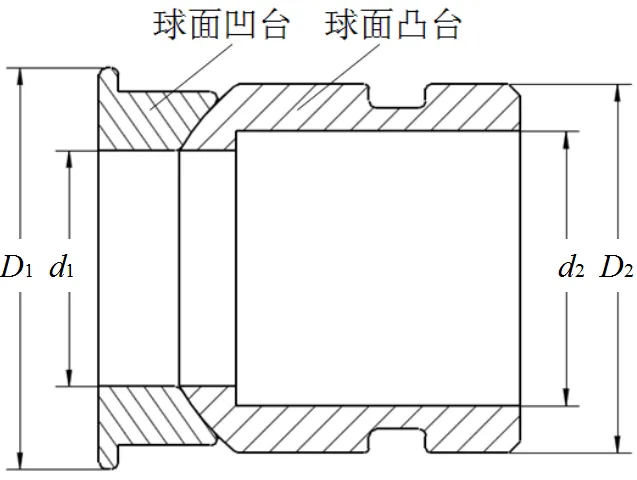
D1、d1—密封端面外径、内径 D2、d2—环形端面外径、内径

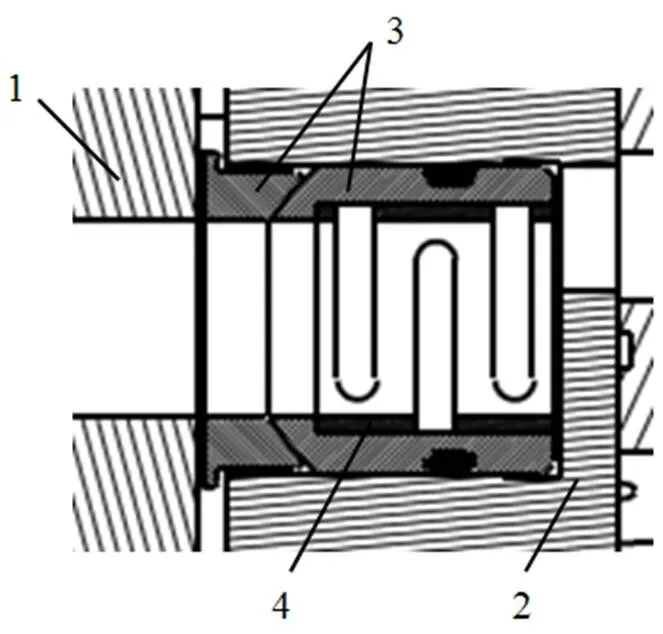
1—固定盘 2—浮板配流盘 3—球面型连通套 4—推力弹簧

球面型连通套的作用在于实现浮板配流盘上的高、低压配流腰形槽与固定盘上的进、出油口的沟通。球面型连通套由球面凹台、球面凸台两部分组成，左端面是与固定盘接触的密封端面，右端面是环形端面，基本结构如图2所示。当伺服泵工作时，作用在球面型连通套环形端面上的液压力对球面凸台有向左的压紧作用，使球面凹台与固定盘保持贴紧，二者形成球面型连通套环形摩擦副，如图3所示。

4 确定压紧系数公式

4.1 剩余压紧力法

环形摩擦副的设计要求是保证球面凹台与固定盘之间存在一定厚度的油膜，但二者间隙不能过大。这与泵缸体、配流盘形成的配流副的设计要求相似，因此借鉴配流副的设计方法，采用剩余压紧力法进行环形摩擦副设计。

剩余压紧力法的基本思想是使摩擦副间压紧力略大于分离力，这样摩擦副既可以紧密接触，又可以在小的比压下工作[2]。

4.2 球面型连通套受力情况

环形摩擦副内液膜对球面凹台有一定的承载力，有促使固定盘与球面凹台两接触端面相互分开的作用。承载力（分离力）open计算公式为：

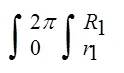
式中：——液膜上的分布压力，Pa；1=1/2；1=1/2。

在工程实际中，有必要考虑振动冲击对球面型连通套的影响。振动冲击有促使固定盘与球面凹台两接触端面相互分开的作用。用冲击加速度与球面型连通套质量的乘积表示振动冲击力a，计算公式为：

a=·（2）

式中：——冲击加速度，m/s2；——球面型连通套质量，kg。

伺服泵工作时，高压油作用在球面型连通套右侧端面上形成液压力y。弹簧推力spring与液压力y都对球面型连通套有向左的压紧作用，促使球面凹台与固定盘相互接触。考虑到液压力y远大于弹簧推力spring，故在此忽略spring不计。闭合力close计算公式为：

close=y=πs(22_22) （3）

式中：s——伺服泵工作压力，Pa；2=2/2；2=2/2。

引入压力脉动系数来体现浮板配流结构内部压力变化，式（3）变为：

close=πs(22_22)=πi(22_22) （4）

式中：——压力脉动系数；i——液膜入口压力，Pa。

综合上述分析，球面型连通套的受力情况如图4所示。

图4 球面型连通套受力情况示意图

4.3 压紧系数计算公式

对球面型连通套受力分析后，得到环形摩擦副压紧系数计算公式：

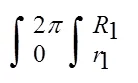
由式（5）可知，压紧系数与压力脉动系数、冲击加速度、球面型连通套质量、液膜上的分布压力有关。其中前三项为定值，而液膜上的压力在液膜模型入口端面处为伺服泵工作压力24MPa，而在出口端面处为泵内腔压力0.5MPa。基于此，可采用Fluent软件对环形摩擦副内液膜进行三维流场数值模拟，利用液膜压力场分布，计算出承载力open，从而确定压紧系数。

5 液膜流场的求解问题

5.1 环形摩擦副内液膜模型

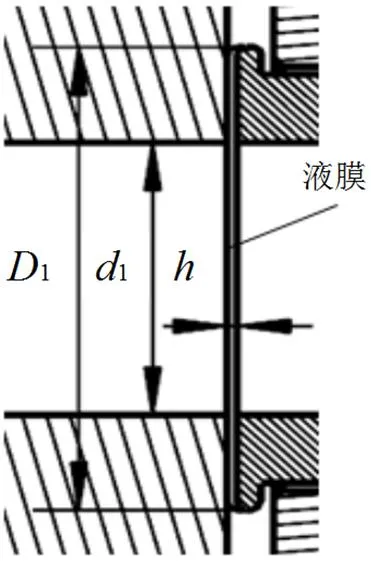
D1、d1—液膜外径、内径 h—液膜厚度

环形摩擦副的密封结构可简化如图5所示。液膜模型为圆环状，厚度为，液膜外径1为15.6mm≤1≤19.6mm，内径1=10mm，基本结构如图6所示。ANSYS软件是目前国际上很流行的大型通用有限元分析软件[3]。本文利用ANSYS中的Fluent软件进行液膜的三维流场数值模拟。按表1内液膜几何参数建立三维模型。环形摩擦副内液膜的工况条件如表2所示。

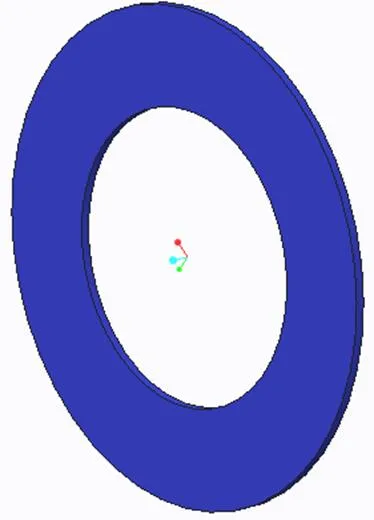
图6 环形摩擦副内液膜模型

表1 液膜几何参数

表2 液膜工况条件

5.2 基本假设

为便于分析，进行以下基本假设：

a. 考虑到液膜厚度为微米级，故在此忽略体积力（如重力、磁力）作用；

b. 视间隙内流体为连续介质，粘度保持不变且为完整的流体膜润滑；

c. 间隙内流体为牛顿粘性不可压流体；

d. 液膜在密封表面无滑动；

e. 液膜厚度保持不变，且不考虑压力沿液膜厚度方向变化。

5.3 控制方程

a. 连续性方程：

式中：——速度矢量在、、方向上的分量。

b. 动量守恒方程：

方向：

方向：

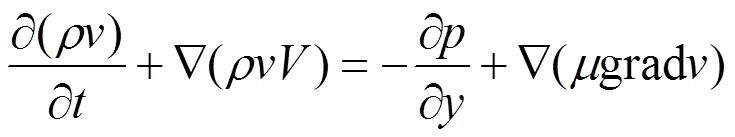
方向：

式中：——微元体所受压力；——流体动力粘度。

5.4 网格划分

利用Creo软件完成液膜三维实体造型设计[4]后，将该实体输出为x_t后缀的文件，然后将该文件导入ANSYS ICEM CFD软件进行六面体结构网格划分。由于液膜厚度为微米级，与液膜内、外径尺寸差4个数量级，所以在液膜厚度方向加密成5层。现已进行网格无关性假设，液膜网格单元数为186140，节点为148400，划分结果如图7所示。

图7 液膜网格划分

5.5 分析求解设置

5.5.1 边界条件

入口边界条件：液膜内端面采用压力进口（pressure-inlet）边界条件。出口边界条件：液膜外端面采用压力出口（pressure-outlet）边界条件。

壁面边界条件：所有壁面均采用标准壁面函数边界条件（wall）。

5.5.2 求解设置

由文献[5]知，利用流动因子可判断流体所处流动状态。当>1时，流动处于湍流状态；当<(9/16)时，流动处于层流状态。

=[(ec/1600)2+(ep/900)2]1/2（10）

ec=/106（11）

ep=r/106（12）

式中：ec——单独考虑库埃特（Couette flow）时的雷诺数；ep——单独考虑泊肃叶（Poiseuille flow）时的雷诺数；——流体密度，kg/m3；——端面旋转线速度，m/s；——液膜厚度，μm；——流体动力粘度，kg/m·s；r——流体径向流速，m/s；

将=870kg/m3，=0，μm，8.7×10-3，r=5m/s带入式（10）、式（11）、式（12）中，经计算发现球面型连通套环形摩擦副内液膜流态为层流。

在Viscous Model模型中选择laminar层流模型。采用SIMPLE算法对速度、压力进行耦合，选用一阶迎风格式对连续性方程、动量方程进行迭代。

6 确定压紧系数范围

图8 摩擦副内液膜压力云图

经Fluent软件数值模拟后得到球面型连通套环形摩擦副内液膜压力场分布，如图8所示。由图8可直观看出：液膜压力呈、轴对称分布，且由内向外依次减小。如图9所示，对后处理软件进一步操作可得到承载力open值。相同工况条件、不同液膜外径1下的液膜承载力open的计算结果如表3所示。

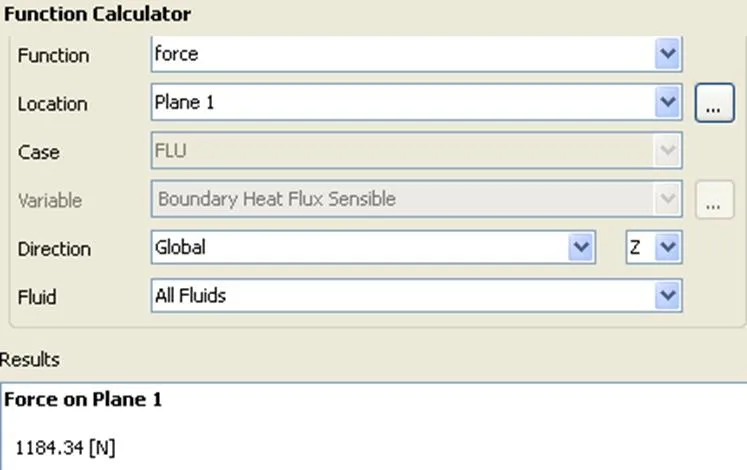
图9 液膜承载力计算

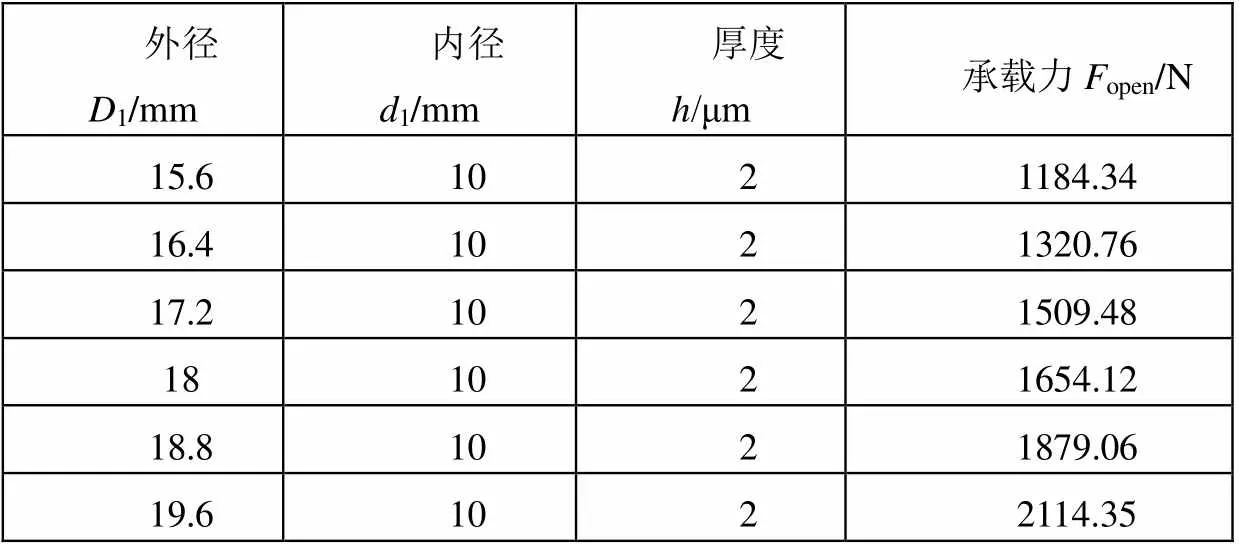
表3 不同液膜外径下的液膜承载力

把球面型连通套球面凸台右侧端面尺寸2、2、液膜入口压力i，表3中open计算结果代入式（5）得到球面型连通套环形摩擦副的压紧系数范围：

/[1.03+4.88×10-4(·)]≤≤/[0.58+4.88×10-4（·）]

式中：——压力脉动系数；——冲击加速度，m/s2；——球面型连通套质量，kg。

7 结束语

本文针对一种可应用于机电静压伺服泵的浮板配流结构，以球面型连通套为研究对象，采用剩余压紧力法进行球面型连通套环形摩擦副设计。在环形摩擦副设计中，压紧系数的确定很大程度上影响浮板配流结构功能的实现。对球面型连通套进行受力分析，得到了工程可用的压紧系数计算公式。为得到压紧系数计算公式中液膜承载力open，利用Fluent软件对环形摩擦副内液膜进行三维流场数值模拟，得到了液膜压力分布，对后处理软件进一步操作得到了承载力open值。将其他设计参数与承载力open计算结果代入压紧系数计算公式，得到了球面型连通套环形摩擦副的压紧系数范围。这种采用理论分析与数值模拟相结合的设计方法，对球面型连通套环形摩擦副的合理设计有一定的参考价值。

1 李元勋，陈卓如，钟廷修. 一种新型倾侧力矩全平衡端面配流机构及其优化设计[J]. 中国机械工程，1999，10(1)：67

2 严金坤，张培生. 液压传动[M]. 北京：国防工业出版社，1979

3 李朔东，马纲. 基于ANSYS的模态分析二次开发及应用[J]. 航天制造技术，2004(5)：8

4 赵佳琪. 基于CREO的虚拟装配路径规划技术研究[J]. 航天制造技术，2016(1)：61

5 Ruddy A.V, Smith S. The mechanism of film generation in mechanical face seals[J]. Tribology International, 1982：227～231

A Design Method of SphericalConnecting Sleeve’s Friction Pair on A Kind of Floating Plate’s Pump

Quan Yunqing Li Jipeng Liu Huixiang Wang Yuhao Zhu Yi

(Beijing Research Institute of Precise Electromechanical Control Equipment, Beijing 100076)

According to the structure of a kind of floating plate, the residual compacting force method is used to design spherical connecting sleeve’s friction pair. After analyzing the spherical connecting sleeve’s loads, the balance factor’s computational formula is provided, and the balance factor’s range is determined based on the flow-field simulation results of Fluent software.

floating plate structure；residual compacting force method；friction pair；flow-field

权云晴（1991），硕士，机械工程专业；研究方向：航天流体控制及自动化。

2018-03-05