一种基于动压变化的火箭助推段弹道设计方法

王 智，马保海，张 婕，熊 伟，宋剑爽

0 引 言

为满足特定的技术验证目的，诸如新型热防护材料的考核验证，需要飞行器全程在大气层内高速飞行来创造需要的飞行环境。飞行器全程在大气层内高速飞行时，一方面主动段动压数值大，变化幅度大；另一方面，传统主动段一级弹道一次负攻角转弯下压的形式已不能满足飞行器全程大气层内飞行的要求。针对以上问题，根据飞行器的飞行特点，本文在弹道设计时采用基于动压变化的二次下压特殊低弹道形式，同时采用序列二次规划算法（Sequential Quadratic Programming，SQP），对基于动压变化的二次下压弹道进行优化设计，可以避免在大动压同时出现大攻角，为飞行器提供良好的飞行环境。通过与传统弹道设计方法的对比分析，验证了所提弹道设计方法在满足给定约束的情况下，减小了主动段最大动压，缩小了动压变化范围，具有较好的工程参考价值。

1 主动段弹道模型

考虑地球为旋转的均质椭球体，忽略风的干扰，采用标准大气模型，在发射坐标系内建立飞行器三自由度质心运动模型。

1.1 弹道计算模型

飞行器主动段运动过程是一个变质量飞行过程，其三自由度质心运动方程为[1]

式中 O为发射坐标系原点与发射点的连接点；x，y，z为飞行器在发射坐标系中的位置三分量；Ox轴为在发射点水平面内指向发射瞄准方向；Oy轴为垂直于发射点水平面指向上方；Oz轴与xOy面相垂直并构成右手直角坐标系； Vx， Vy， Vz为飞行器在发射坐标系中的速度三分量； ROx， ROy， ROz为发射点地心矢径在发射坐标系中的三分量； gx， gy， gz为引力加速度在发射坐标系中的三分量；P为发动机推力；X，Y，Z分别为气动阻力、升力和侧向力；m为飞行器质量； m0为飞行器初始质量；m˙为质量秒消耗量； GB为箭体坐标系至发射坐标系的转换矩阵； GV为速度坐标系至发射坐标系的转换矩阵；A为离心惯性力矩阵；B为哥氏惯性力矩阵。

1.2 飞行程序角设计

飞行程序角设计是弹道优化设计的关键，也是弹道参数优化问题的主要对象[2～4]。

飞行器全程在大气层中高速飞行时，主动段动压数值大，变化幅度大，为便于程序角设计，采用跟踪程序攻角的方式。同时在进行程序攻角设计时，为使飞行程序能反映动压及其变化情况，主要根据动压的变化情况进行设计。主动段程序攻角设计曲线见图1。

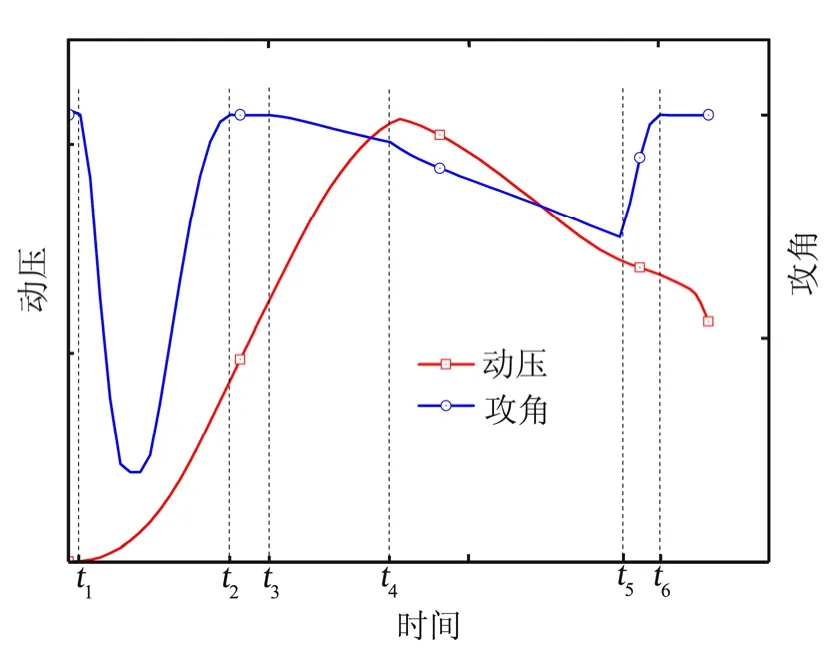
图1 主动段程序攻角与动压曲线Fig.1 Curve of Attack Angle and Dynamic Pressure for Boost-phase Trajectory

点火起飞后，零攻角垂直飞行至1t时刻。1t时刻后，动压Q呈现增大趋势，为避免在大动压时出现大攻角，在动压增大一定幅度后，即2t时刻，攻角恢复到零，从而实现飞行器在出现动压最大值及其附近时的攻角数值比较小，为飞行器提供良好的飞行环境。在1t～2t时间段，进行第1次程序负攻角转弯飞行，程序攻角设计为如下形式：

式中mα为第1次转弯攻角绝对值的最大值；mt为攻角达到极值mα的时间。

在23～tt时间段，飞行器保持零攻角重力转弯飞行，3t取在接近动压最大值处。

在35～tt时间段，飞行器进行第2次程序负攻角转弯飞行。为有效调整飞行动压的变化情况，通过时间变量4t将第2次程序负攻角转弯飞行分成两段，即第2次程序负攻角转弯的第1段和第2段。5t取在动压下降段变平缓处。程序角设计为如下形式：

式中 ϕcx0，ϕcx1分别为t3时刻和t4时刻的程序角；ϕ˙cx1，ϕ˙cx2分别为二次下压第一段和第二段俯仰程序角变化率；ωz为地球自转角速度在发射坐标系z轴的分量；θ为弹道倾角。

在56～tt时间段，飞行器进行攻角归零飞行，以使在分离时刻攻角为零，为分离创造良好的条件。6t取在发动机关机前4～5 s之间。

综上所述，时间点1t～6t、mα、二次下压第1段和第2段俯仰程序角变化率cx1ϕ˙和cx2ϕ˙决定了主动段程序角的变化规律。依据各种设计指标要求，mα、4t、1cxϕ˙和cx2ϕ˙由弹道优化得到。由于第一次下压段动压较小，第二次下压段动压较大，为避免第二次负攻角转弯出现较大的攻角，需要 ϕ˙cx1＜ϕ˙cx2。

2 优化问题建模

2.1 性能指标

为给全程大气层内高速飞行器创造较好的飞行环境，减小姿态控制系统和载荷设计难度，需要避免在大动压时出现大攻角。因此，在进行二次下压弹道优化设计时，目标函数选择为

2.2 优化控制变量

选取变量mα，4t，cx1ϕ˙，cx2ϕ˙和射向角0A作为优化参数，因此，优化控制变量为

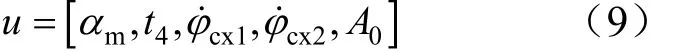
2.3 约束条件

考虑可实现性，控制变量应满足如下的约束条件：

此外，由于弹道采用低弹道形式，要求飞行高度满足：

式中ch为给定的最大飞行高度。

同时落点航程偏差LΔ和落点横程偏差HΔ满足：

3 主动段弹道优化

弹道优化分为静态优化和动态优化问题。严格来讲，弹道优化是一个动态优化问题，但由于弹道优化自身的复杂性，采用动态优化求解面临较大难度。因此通常将弹道优化转化为静态优化问题，再通过数值方法求解[5,6]。

弹道优化转化的数值方法主要有间接法和直接法两种。间接法根据 Pontryagin极小值原理将最优控制问题转化为两点边值问题，其求解的精度较高，且其解满足一阶最优性必要条件。但由于飞行器数学模型复杂，协态方程与横截条件推导过程较为复杂和繁琐；同时协态量初值无实际物理意义，其初值难以估计。直接法采用离散化方法将连续的弹道优化问题转化为非线性规划问题，然后采用数值方法对非线性规划问题进行求解。直接法不需求解最优解的必要条件，操作简单；同时具有较好的通用性和鲁棒性[7～10]。

求解非线性规划问题的数值方法包括以可行方向法、梯度下降法、罚函数方法、动态规划法、SQP法等为代表的精确算法和以遗传算法、进化策略、模拟退火算法、神经网络算法等为代表的现代启发式算法[11～14]。其中，SQP算法是一种有效的求解非线性规划问题的工具，是飞行器弹道优化的主流方法。

SQP算法将有约束的优化问题通过拉格朗日函数转化为无约束的优化问题，并将原优化问题通过求解Lagrange极小值方程转化为二次规划问题，最后通过拟牛顿迭代算法与 BFGS（Broyden Fletcher Goldfarb Shanno）更新算法完成计算[15～18]。非线性规划问题可表示为

非线性规划问题对应的二次规划子问题可表示为

式中 d为搜索方向； ∇ J (uk)， ∇ c (uk)， ∇ p (uk)分别为函数 J (u)， c (u)和 p (u)在 uk处的梯度； Bk矩阵为Lagrange函数的Hessian阵的良好近似。

本文通过选择程序角中的特征参数作为优化变量，将弹道优化转化为参数优化问题，利用SQP算法求解。弹道优化流程如图2所示。

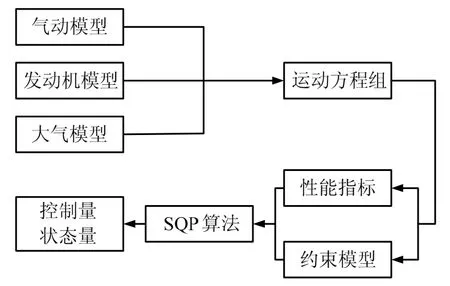
图2 弹道优化流程Fig.2 Flow Chart of Trajectory Optimization

4 仿真分析

分别对基于动压变化的二次下压优化弹道和传统弹道设计结果进行对比分析。主要特征参数比较见图 3～6。

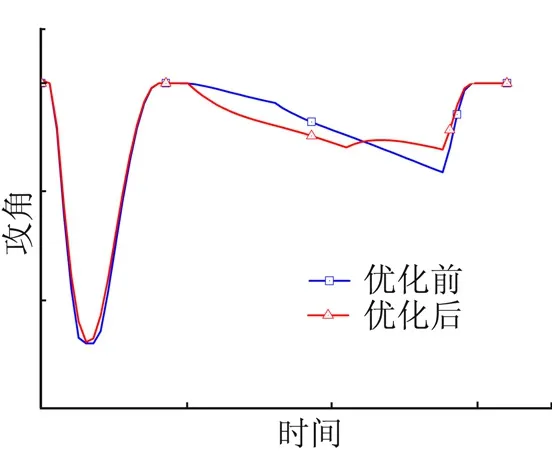
图3 主动段攻角随时间变化曲线Fig.3 Curve of Attack Angle for Boost-phase Trajectory

图4 主动段动压随时间变化曲线Fig.4 Curve of Dynamic Pressure for Boost-phase Trajectory

图5 主动段动压攻角乘积随时间变化曲线Fig.5 Curve of Product of Dynamic Pressure and Attack Angle for Boost-phase Trajectory

图6 高度随航程变化曲线Fig.6 Curve of Height and Range

由图3～6可以看出，采用SQP算法对基于动压变化的二次下压弹道进行优化设计，在满足最大飞行高度和落点等飞行约束的同时，第2次下压攻角绝对值最大值减小，最大动压减小5%，动压与攻角乘积绝对值的最大值减小8%，验证了所提弹道设计方法的有效性。

5 结 论

本文首先阐述了基于动压变化的二次下压特殊低弹道优化设计方法，然后通过仿真分析，获得以下结论：

a）采用基于动压变化的二次下压程序攻角设计，可使飞行程序反映动压及其变化情况；

b）采用基于动压变化的二次下压弹道优化设计时，在飞行约束满足的同时，第二次下压攻角绝对值最大值、最大动压和动压与攻角乘积绝对值最大值均有所减小，验证了所提弹道设计方法的有效性，具有较好的工程应用价值。