火箭基组合循环高超声速飞行器爬升-巡航全局轨迹优化研究
郑 雄,刘竹生,杨 勇,雷建长,李争学
0 引 言
火箭基组合循环(Rocket Based Combined Cycle,RBCC)推进系统将火箭发动机和冲压发动机有机结合在同一流道中,具有引射(Ejector)、亚燃冲压(Ramjet)、超燃冲压(Scramjet)和纯火箭(Rocket)等多个工作模态,能充分发挥火箭发动机大推重比和冲压发动机高比冲的优势,可执行大空域、宽速域飞行任务,是未来高超声速巡航飞行器(Hypersonic Cruise Vehicle,HCV)以及单级入轨(Single Stage To Orbit,SSTO)重复使用运载器的理想动力系统。
相比于无动力或传统火箭动力高超声速飞行器,RBCC高超声速飞行器的轨迹优化除了要解决飞行高度、速度变化大,飞行约束多、复杂,飞行轨迹对控制变量高度敏感等难题,还面临RBCC发动机工作模态多,各模态性能差异大,飞行轨迹与动力相互耦合的特有困难,这些使得RBCC高超声速飞行器的轨迹优化极具挑战性,为此必须选择和发展一种行之有效的方法。
目前,对RBCC可重复使用运载器上升段轨迹设计与优化进行了较多研究[1~4],而对RBCC高超声速巡航飞行器的轨迹优化研究较少。王厚庆等[5]通过求解纵向平面内的质点运动方程,对RBCC巡航飞行器的飞行轨迹和有效载荷能力进行了分析,但没有采用优化方法,无法获得性能最优的飞行轨迹。吕翔等[6]考虑RBCC发动机性能与飞行状态之间的耦合,提出基于马赫数-动压参考曲线的RBCC巡航飞行器爬升段轨迹设计方法,同样没有采用优化方法,不能充分挖掘飞行器总体性能。李响等[7]利用遗传算法对RBCC高超声速导弹的爬升-巡航航程进行优化,但没有考虑动压、过载、热流密度等约束,所得结果可能出现不可行点。
本文以RBCC高超声速巡航飞行器为研究对象,针对其爬升-巡航全局轨迹优化问题,提出一种“粒子群优化算法+伪谱法”的嵌套优化策略。基于该策略,在以全程燃料最省为优化目标的条件下,不仅能优化飞行攻角和发动机节流阀开度,还能得到飞行器的最佳巡航高度和马赫数,在模型求解过程中全面考虑RBCC发动机性能与飞行状态的耦合及动压、过载、热流密度等约束,最后通过仿真算例,验证了所提方法的有效性。本文研究旨在结合RBCC高超声速巡航飞行器的特点提出轨迹优化策略,建立优化模型,通过对结果进行分析,为此类新型飞行器的总体设计及轨迹优化提供参考。
1 任务剖面及优化策略
1.1 任务剖面
考虑RBCC高超声速巡航飞行器任务剖面示意图如图1所示。

图1 RBCC巡航飞行器任务剖面Fig.1 The Mission Profile of RBCC Cruise Vehicle
从图 1可见,飞行器由机载水平发射,经引射、亚燃冲压、超燃冲压 3个模态加速爬升到期望高度和马赫数进行巡航飞行,飞抵目标空域后下压攻击,对目标实施精确打击。为简化考虑,本文只对爬升-巡航轨迹进行研究,而不考虑下压攻击段。鉴于RBCC发动机各模态性能差异大的特点,可将爬升段进一步划分为引射爬升段、亚燃冲压爬升段和超燃冲压爬升段。
综上,RBCC高超声速飞行器的爬升-巡航轨迹包括以下4个阶段:
a)引射爬升段。该阶段从水平发射点火加速至亚燃冲压模态的启动条件,RBCC发动机在引射模态比冲较小,推进效率低,为避免长时间的低空阻力消耗,需要飞行器尽快加速和爬高。增大攻角可提高爬高速度,但同时会增大飞行阻力,减小加速度,还可能会造成法向过载超出限定值。因此,攻角的取值需要在爬高和加速之间折中考虑。
b)亚燃冲压爬升段。该阶段RBCC发动机比冲最大,推进效率最高,为充分发挥此优势,应使飞行器在该阶段的速度增量和高度增量最大。本段设计难点在于发动机性能对飞行状态非常敏感,如果爬高过快而加速太慢,则发动机进气量减少,性能降低,而如果爬高过慢而加速太快,由于大气阻力太大,同样会降低飞行器性能。
c)超燃冲压爬升段。该阶段飞行器速度大、高度高,对爬高和加速的要求不大,主要任务是使飞行器从爬升段平稳过渡到巡航段。本段的工作时间较短,其轨迹设计难点是终端必须满足巡航起始条件。
d)巡航段。该阶段飞行器保持等高等速飞行,其飞行距离占总射程的 90%左右,不同巡航高度和马赫数下,发动机性能以及飞行器所受阻力差异较大。因此,有必要对巡航高度和马赫数进行优化,以使飞行全程消耗的燃料最省。
总之,在RBCC高超声速飞行器爬升-巡航全局轨迹优化过程中,不仅要考虑最佳巡航高度、马赫数的确定,还要考虑发动机各模态的工作范围限制以及动压、过载、热流密度、控制变量的取值范围等约束,这些导致RBCC高超声速巡航飞行器燃料最省轨迹的确定需要在诸多约束之间权衡协调。
1.2 优化策略
RBCC高超声速巡航飞行器的爬升-巡航全局轨迹优化是一个多控制变量、多阶段、多约束的最优控制问题。针对最佳巡航高度和马赫数的确定,考虑到粒子群优化[8](Particle Swarm Optimization,PSO)算法概念简单、智能背景深刻、全局收敛性好的优点,本文拟采用粒子群优化算法。而对于爬升-巡航这一多阶段多约束的轨迹优化问题,鉴于伪谱法(Pseudospectral Method,PM)在航空航天领域各类飞行器轨迹优化中的广泛应用[9],本文拟采用伪谱法。据此,本文提出“粒子群优化算法+伪谱法”的嵌套优化策略,同时优化巡航高度、马赫数、飞行攻角及发动机节流阀开度。嵌套是指伪谱法嵌套在粒子群优化算法中,被其不停调用,具体流程如图2所示。
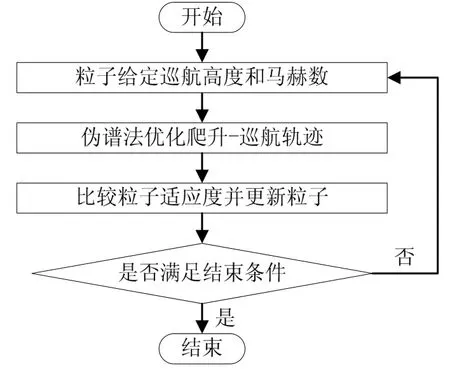
图2 嵌套优化策略流程Fig.2 The Process of Nested Optimization Strategy
该嵌套优化策略的流程包括以下4步:
a)粒子群算法中的粒子对巡航高度和马赫数赋值,以此作为爬升和巡航的中转条件;
b)伪谱法进行多阶段多约束的爬升-巡航全局轨迹优化,得到射程末端的飞行器质量,并将其作为粒子的适应度;
c)比较各粒子适应度,并据此更新粒子;
d)判断是否满足结束条件,若否,返回a,若是,结束。
2 轨迹优化数学模型
2.1 动力学模型
将RBCC高超声速飞行器看作铅垂平面内运动的可控质点,视地球为圆球,并忽略自转,则飞行器的动力学模型为

式中 H,V,θ,m,DL,r,α,τ分别为飞行高度、速度、速度倾角、飞行器质量、射程、地心距、攻角和发动机节流阀开度;eR,0g,g分别为地球平均半径、海平面重力加速度和当地重力加速度;D,L分别为阻力和升力, D =qSCD, L = q SCL,其中,q为动压,S为参考面积, CD和 CL分别为阻力系数和升力系数;P, Isp分别为 RBCC发动机推力和比冲,P=P(M a,H),Isp=Isp(Ma,H),是关于马赫数和高度的插值表,由RBCC发动机性能分析或试验给出。
2.2 控制变量选择
巡航高度 HCruise和马赫数 M aCruise的取值对RBCC巡航飞行器总体性能影响较大,因此选择二者作为粒子群优化算法的控制变量。此外,在用伪谱法优化爬升-巡航轨迹时,为便于加入对攻角和发动机节流阀开度的约束,避免优化结果中出现取值变化过快的情况,可将α,τ取为状态变量,从而引入新的控制变量uα和uτ:

因此,在伪谱法优化爬升-巡航轨迹时,状态向量x=[H,V,θ,m,LD,α,τ],控制向量 u = [uα, uτ]。
2.3 约束模型
2.3.1 控制变量约束
粒子群优化算法的控制变量为[HCruise, MaCruise],伪谱法的控制变量为[uα,uτ],它们所受约束如下:
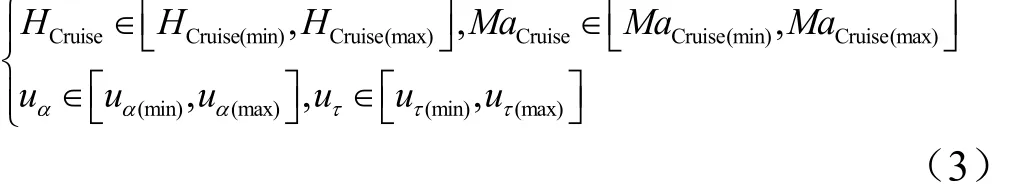
2.3.2 过程约束
过程约束是指飞行器在飞行过程中任何时刻都必须满足的约束条件,否则将直接影响甚至破坏飞行器。本文过程约束除了有一般的动压约束、法向过载约束、热流密度约束外,还有为保证RBCC发动机正常工作的攻角、发动机节流阀开度取值约束以及飞行高度约束,具体形式如下:
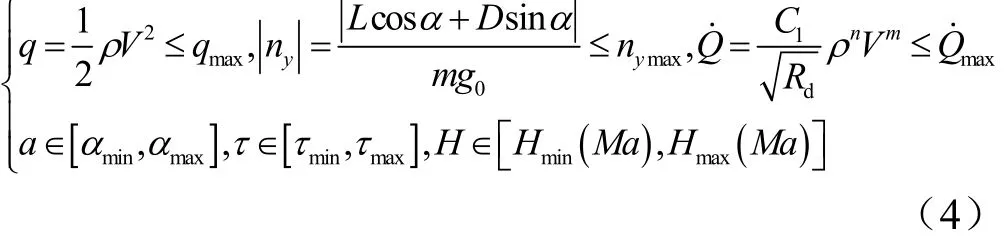
式中 ρ为大气密度;C1为与飞行器特性相关的常数;Rd为飞行器头部曲率半径;m,n为常数; Hmin(M a),Hmax(M a)随马赫数变化,其规律由RBCC发动机性能分析或试验给出。
2.3.3 边界约束
边界约束包括初始边界和终端边界约束。初始边界约束即RBCC高超声速飞行器发射时刻状态变量的初值,是完全给定的;终端边界约束是指飞行器在轨迹终点需满足的条件,本文中包括高度、速度、速度倾角和射程。综上,边界约束表示如下:
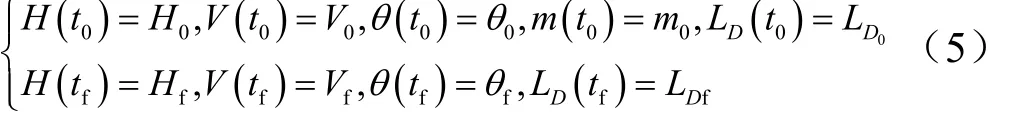
式中 t为时间;下标0,f分别表示开始和结束。
2.3.4 连接点约束
为使RBCC巡航飞行器的4个阶段光滑衔接,需要保证相邻两阶段连接点处的状态量和控制量对应相等。此外,在超燃冲压爬升段的末端,飞行器应达到巡航条件。因此,连接点约束条件为
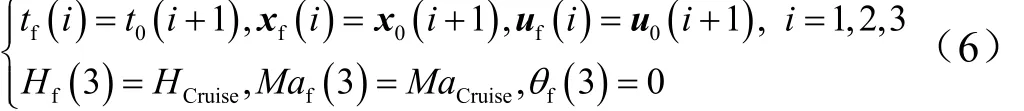
式中 i为飞行器飞行的第i个阶段。
2.4 性能指标
选择在满足既定射程的前提下,燃料最省为优化指标,其等效于 − m (tf)取极小值,故针对粒子群优化算法和伪谱法,性能指标均取为

3 优化算法基本原理
此节介绍粒子群优化算法和Radau伪谱法的基本原理,其中涉及很多变量,各变量的含义在每种方法中都进行了说明,应分别理解。
3.1 粒子群优化算法基本原理
设 PSO 算法中有N个粒子,每个粒子k(k = 1 ,2,… ,N )表示优化问题解空间中的一个备选解。所有粒子都有自己的位置速度以及一个由目标函数J = f ( x ( k))计算得到的适应度,其中n为待优化变量的个数,通过比较各粒子的适应度来判断粒子的优劣。根据每个优化变量的取值范围 xi∈ [ ai, bi] , i = 1,2,… ,n ,对粒子位置和速度的限制如下:

设 NIT为 PSO算法总迭代次数,在任一次迭代j(j = 1 ,2,… ,NIT)中,各粒子依据自身记忆(粒子k迄今为止搜索到的最优位置)和粒子群的记忆(整个粒子群迄今为止搜索到的最优位置)来更新自身的位置,以搜索设计空间内的最优解。标准PSO算法的粒子速度与位置更新公式如下:

式中0c为惯性权重系数;1c为粒子跟踪自身历史最优值的权重系数;2c为粒子跟踪粒子群历史最优值的权重系数;1r,2r为(0,1)内的随机数。
结束条件根据具体问题选择达到最大迭代次数或粒子群搜索到的最优位置满足预期精度。
综上,PSO优化算法的计算流程可归纳为如图3所示。
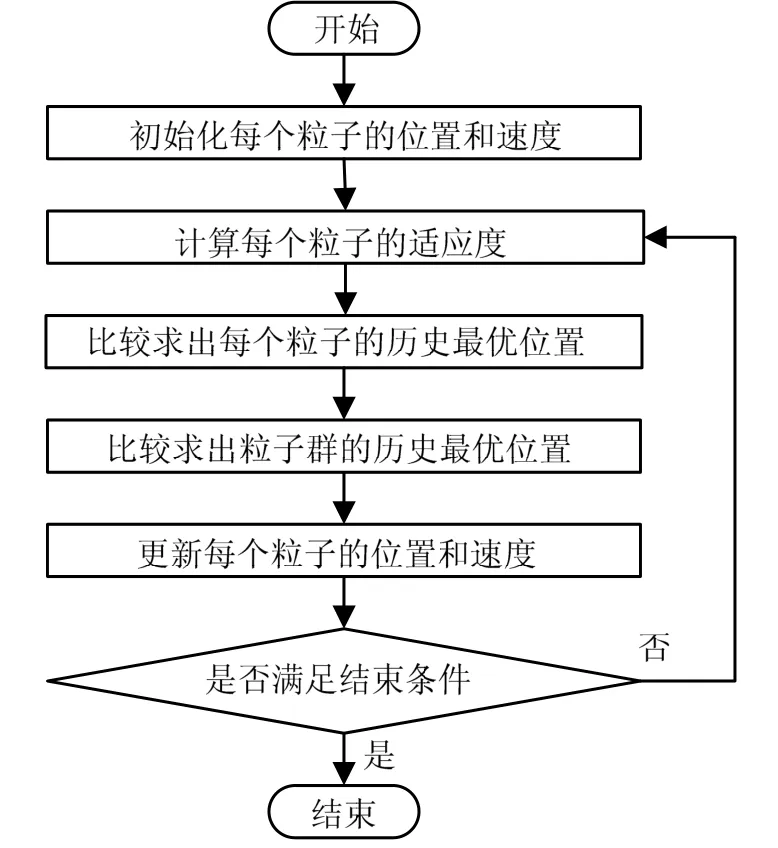
图3 粒子群优化算法计算流程Fig.3 The Computation Process of PSO Algorithm
3.2 Radau伪谱法基本原理
伪谱法采用全局插值多项式的有限基在一系列离散点上近似状态变量和控制变量,将连续时间最优控制问题转换为非线性规划(Nonlinear Programming,NLP)问题进行求解。本文选择 Radau伪谱法转换最优控制问题,这是由于Radau伪谱法与Gauss伪谱法或Lobatto伪谱法相比,更易满足区间切换点上状态变量保持连续这一条件[10]。
Radau伪谱法将最优控制问题的时间区间[t0,tf] 分成K段,并将每段的时间区间 t ∈ [ tk−1,tk]转换到 τ ∈[− 1,1]上,于是对应有:
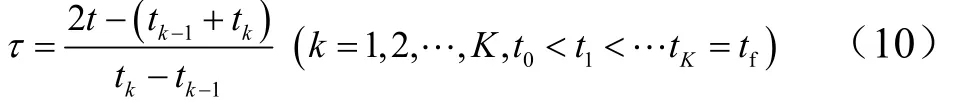
使用Legendre-Gauss-Radau(LGR)离散点来离散状态变量和控制变量,对第 k(k = 1 ,2,…, K )段,选取 Nk个配点它们是的根,其中为 Nk阶Legendre多项式,表达式如下:
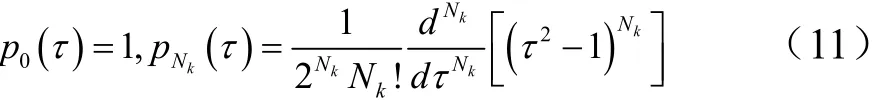
以为插值节点,分别用Nk, Nk−1阶拉格朗日插值多项式为基函数来近似状态变量和控制变量,即:
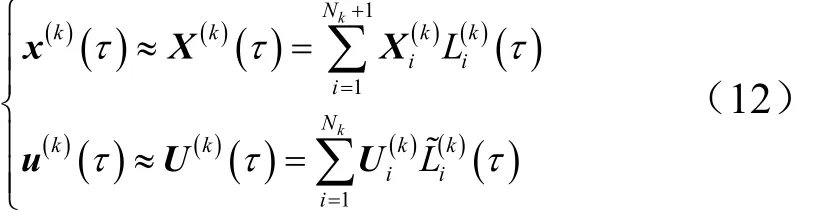
式中,分别为状态变量和控制变量在插值节点处的值;(τ),(τ)表达式如下:

将动力学微分方程约束转化为代数方程约束:
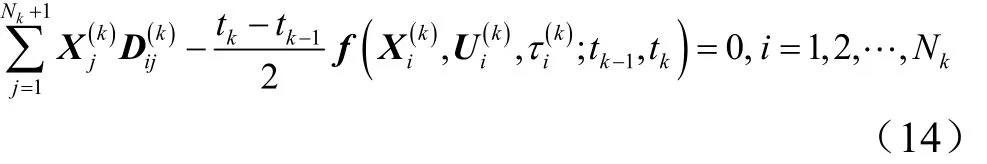
式中第k段处 N ×(N +1)阶Radau伪谱微分kk矩阵。
末值型性能指标函数近似为

过程约束为
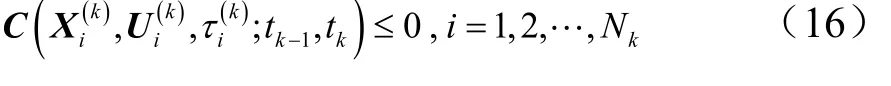
边界约束为
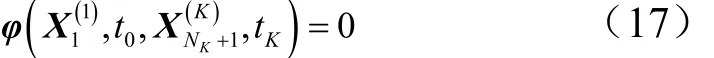
此外,为保证相邻两段的连续性,需满足其中 k =1,2,…,K −1。
基于上述离散过程,RBCC高超声速巡航飞行器的多阶段多约束轨迹优化问题转化为NLP问题,可以采用SNOPT软件包求解。
4 仿真算例
4.1 仿真条件
根据上文的任务剖面,RBCC高超声速巡航飞行器先通过载机挂飞到10 km高度,随后被水平发射。初始马赫数、速度倾角、质量分别为0.8、0°、1500 kg;巡航高度和马赫数的取值范围分别为 25~30 km、Ma=6.5~7;期望射程为1500 km。飞行过程中,攻角和发动机节流阀开度的取值范围分别为-2~6°、0.2~1;过程约束为飞行动压小于等于90 kPa,法向过载小于等于3,热流密度小于等于2500 kW/m2。RBCC发动机使用碳氢燃料,引射模态和亚燃冲压模态的转换马赫数为3,亚燃冲压模态和超燃冲压模态的转换马赫数为6,各模态适宜工作范围由RBCC发动机性能分析得出。设定粒子群优化算法的粒子数10,迭代次数6,c0=0.729,c1= c2=2。在Radau伪谱法中,对RBCC高超声速飞行器爬升-巡航飞行轨迹的每一阶段,均选取插值节点数21。
4.2 结果分析
图4为巡航高度、马赫数优化结果。由图4可知,在第2代时全局最优粒子出现,第4代时所有粒子均收敛于全局最优粒子,从而得到飞行器最佳巡航高度和马赫数为30 km、Ma =6.5,此时飞行器剩余质量最大,为749.1 kg。分析认为,RBCC高超声速飞行器在25~30 km的巡航高度范围内,高度越高,大气密度越低,所受阻力越小;此外,当以Ma=6.5~7超燃冲压巡航时,RBCC发动机的比冲随马赫数增大而减小,因此,30 km、Ma =6.5的巡航状态下燃料使用效率最高。虽然具体第几代出现全局最优粒子会受到初代粒子分布的影响,但从粒子数较多及初值取值的随机性这两点考虑,PSO算法在对RBCC高超声速飞行器巡航高度和马赫数寻优时总能快速收敛。

图4 巡航高度、马赫数优化结果Fig.4 The Optimization Result of Cruise Altitude and Mach Number
巡航高度、马赫数取最优值时,由Radau伪谱法得到的飞行器控制变量、飞行状态以及过程约束变化规律如图5所示。由图5a~5b可知,攻角和发动机节流阀开度均在限定的取值范围内,且变化平缓,易于实现;在引射爬升段和亚燃冲压爬升段,RBCC发动机处于满推状态,表明此段飞行对爬高和增速需求较大,而在巡航段,飞行器高度较高,大气较稀薄,发动机节流阀开度取较小值就能实现推阻平衡。由图 5c~5g可知,飞行器能稳定爬升、加速,并平滑过渡到巡航段,巡航高度和马赫数达到期望值;飞行器射程为1500 km,满足任务要求,全程飞行耗时819.4 s,可实现快速抵近;引射爬升段、亚燃冲压爬升段和超燃冲压爬升段燃料消耗量分别为255 kg、122 kg、38 kg,可见在爬升段中,引射模态消耗燃料最多,占比61.45%,而亚燃冲压模态消耗较少燃料就实现了高度和速度的大幅增加,增幅分别为11.42 km、910 m/s,各自占总爬高量和加速量的57.1%、52.86%;爬升-巡航全程飞行消耗燃料 750.9 kg,占飞行器总质量的50.06%。由图 5h可知,飞行器马赫数-高度曲线始终处于RBCC发动机正常工作范围内,满足动力对飞行轨迹的约束,此外,还能看出,在飞行初期,飞行器处于先加速后爬高的状态,分析认为,尽早加速以更快进入亚燃冲压模态,有利于节省燃料。由图 5i~5k可知,飞行过程中动压、法向过载、热流密度均满足约束条件,动压最大值70.5 kPa出现在亚燃冲压爬升段,这是因为该阶段飞行器速度大,同时大气仍较稠密;法向过载最大值2.62出现在引射爬升段,对照攻角剖面可看出,这主要由攻角较大引起;热流密度最大值2280 kW/m2同样出现在引射爬升段,其在该段的变化规律是先增大后减小,表明速度增加和大气密度减小先后起主要作用。
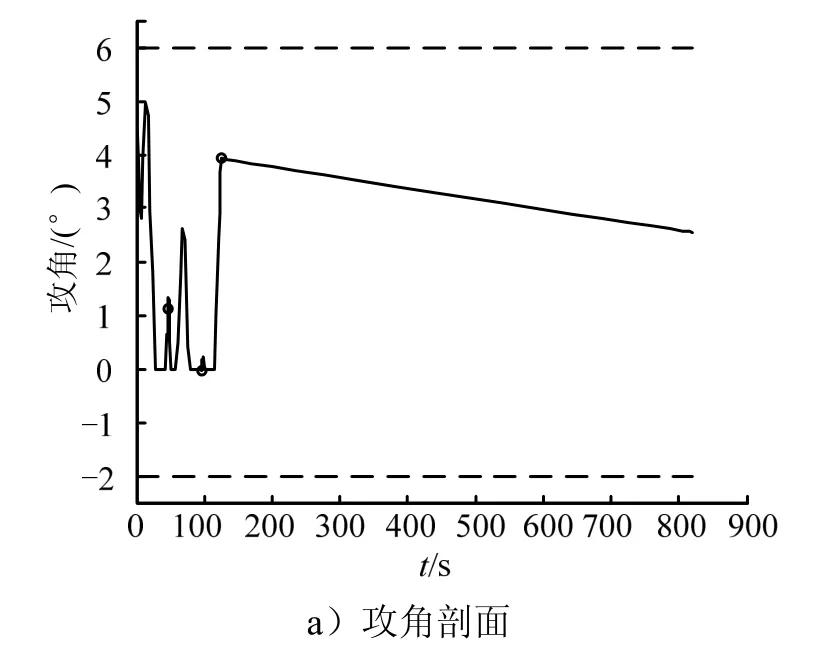
图5 爬升-巡航轨迹优化结果Fig.5 The Optimization result of Climb-cruise Trajectory
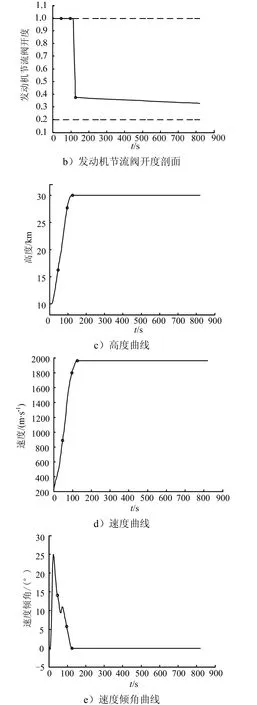
续图5
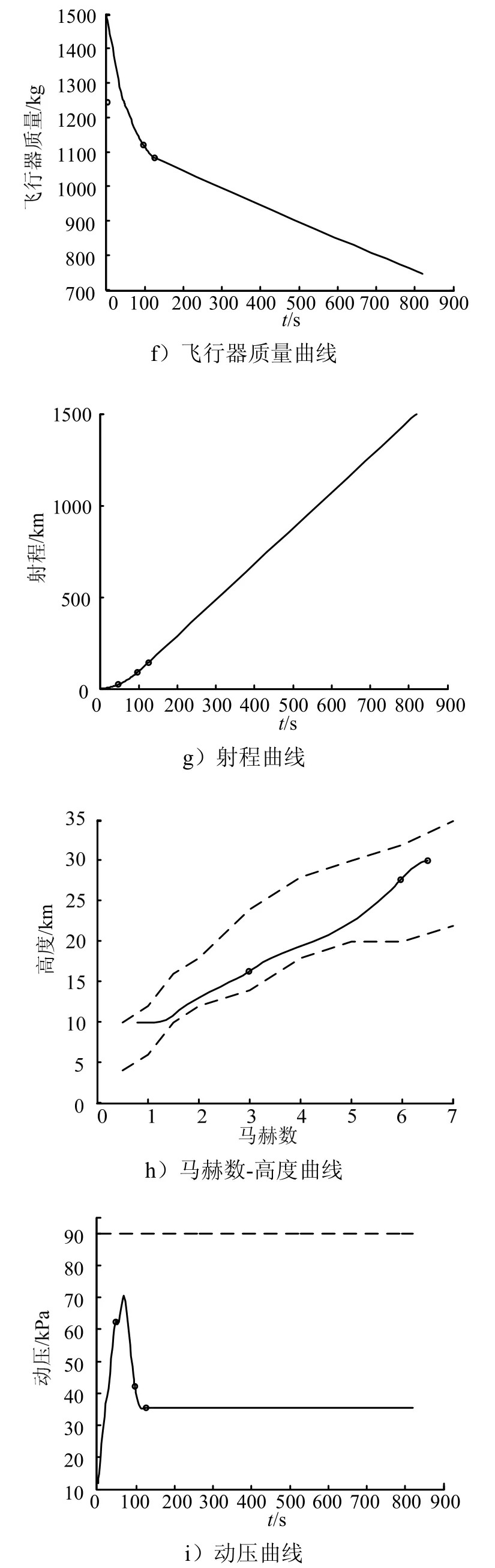
续图5

续图5
5 结 论
本文以 RBCC高超声速巡航飞行器为研究对象,对其爬升-巡航全局轨迹优化问题进行研究,所得结论如下:
a)“粒子群优化算法+伪谱法”的嵌套优化策略能很好地解决同时优化巡航高度、马赫数、飞行攻角以及发动机节流阀开度这一难题,所得结果合理可行;
b)对巡航高度和马赫数的优化结果表明,在25~30 km、Ma=6.5~7的巡航包线内,为使RBCC高超声速飞行器爬升-巡航全程飞行燃料最省,巡航高度应尽可能高,而巡航马赫数应尽可能低;
c)优化所得爬升-巡航轨迹符合 RBCC高超声速飞行器各阶段工作特点,满足所有约束条件,表明伪谱法对RBCC高超声速飞行器的轨迹优化问题具有较好的适应性;
d)RBCC高超声速巡航飞行器具有全程自主飞行、无需助推、高马赫数巡航的特点,能快速抵近目标,是未来高超声速飞行器的重要发展方向。

