Heisenberg群上加幂权Hardy算子的精确估计

陈国霁,董建锋

平均算子在调和分析中起着基本性的作用,是现代调和分析的核心之一.Hardy算子是一类最为典型的平均算子,其中欧氏空间上Hardy算子的最佳常数问题也是学界的一个研究热点[1-6].

Heisenberg群在数学和物理中都有重要应用:在数学上,其与多复分析、表示论和偏微分方程(Fourier变换、拟微分算子)相关;在物理上,其与量子力学相关[7].Wu等[8]证明了Hardy算子在Lp(Hn)函数空间的有界性,并给出了其最佳常数.幂权Lp(Hn,|x|αhd x)空间也是一类重要的函数空间.本研究探讨了Hardy算子在函数空间上的最佳常数及其与维数、幂权指数的关系.受Zhao等[6]的方法启发,本研究获得了Hardy算子在Lp(Hn,|x|αhd x)的有界性和(p,p)型的最佳常数,以及弱(1,1)型的最佳常数的上下界.

一维Hardy算子[9]定义为

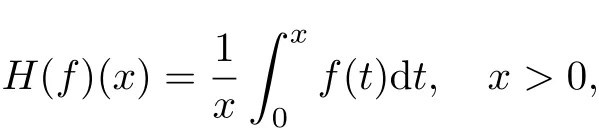
式中,f是R+上的局部可积函数.由著名的Hardy积分不等式[10]可知,

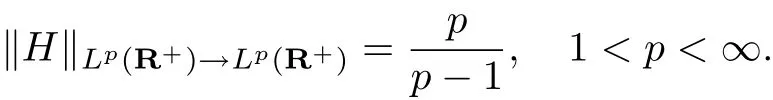
Chirst等[3]研究了Rn上的n维Hardy算子:

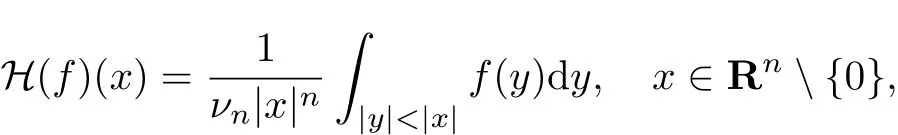
式中,f是非负函数和,νn是Rn中单位球的体积.同时,Chirst等[3]还获得了Hardy算子的最佳常数:

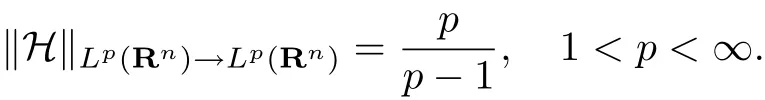
1 预备知识

定义 1 Hn=(R2n×R,·)称为Heisenberg群,其中对任意x=(x1,x2,···,x2n,x2n+1),y=(y1,y2,···,y2n,y2n+1)∈ R2n×R,有

在Hn中定义伸缩δ:R+×Hn→Hn,

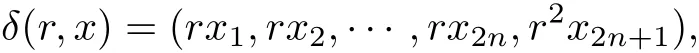
记为δrx.

在Hn上的测度是R2n×R上的Lebesgue测度.对于任意可测集E⊆Hn,E的测度记为|E|,有

式中,Q=2n+2称为齐次维数.

Hn上可以定义一个范数,即

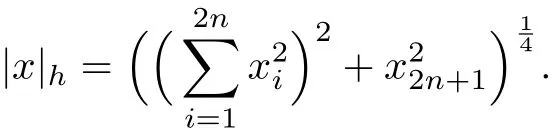
由此可以诱导一个如下的不变距离:

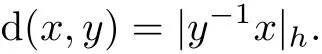
对于x∈Hn,r＞0,定义Hn上球心为x和半径为r的开球为

其球面定义为

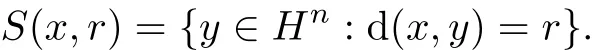
根据上述定义,可得

式中,νQ是Hn上单位球B(0,1)的体积,即

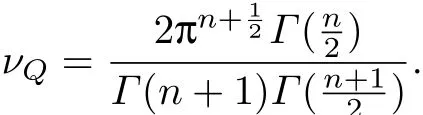
单位球面S(0,1)通常简记为SQ−1,则SQ−1的面积为ωQ=QνQ[11].

定义Heisenberg群Hn上的Hardy算子如下.

定义2 令f是Hn上的局部可积函数,则Hn上的n维Hardy算子定义为

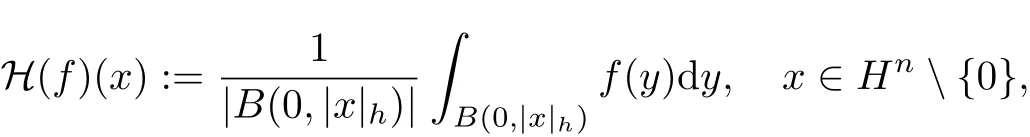
式中,B(0,|x|)表示中心是原点、半径为|x|的开球,|B(0,|x|)|表示开球B(0,|x|)的体积.

定义加幂权弱函数空间如下.

定义 3 令f为Hn上任意可测函数,则L1(Hn,|x|αhd x)的弱空间L1,∞(Hn,|x|αhd x)由所有Hn上的函数f组成,且满足

2 引理和定理

引理1[8]对于任意f∈Lp(Hn),令

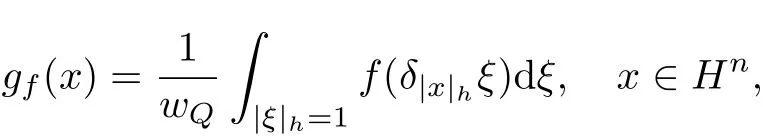
则gf(x)是一个径向函数,且Hf(x)=Hgf(x).

引理2 设f是Hn上的非负可测函数,则对于任意α∈R,有

式中,+=1,1≤p,q≤∞,并设定=0.

证明 利用广义Minkowski不等式和H¨older不等式,可得

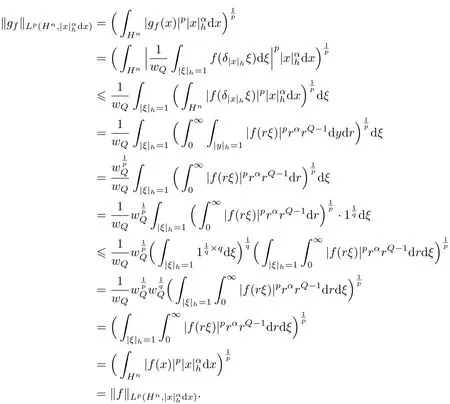
通过引理1和引理2,可得

因此只需考虑径向函数.

定理 1 记 ‖ ·‖Lp(Hn,|x|αhd x)→Lp(Hn,|x|αhd x) 表示算子在幂权函数空间 Lp(H n,|x|αhd x) 上的范数,则Hardy算子H在Heisenberg群幂权函数空间Lp(Hn,|x|αhd x)上的主要结果如下:

(1)当1＜p＜∞,α＜(p−1)Q时,

(2)当p=∞时,

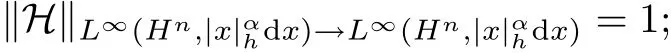
(3)当p=1,−Q＜α＜0时,

证明 (1)当1＜p＜∞,α＜(p−1)Q时,假设f∈Lp(Hn,|x|αhd x)是径向函数.利用广义Minkowski不等式可得

因此,

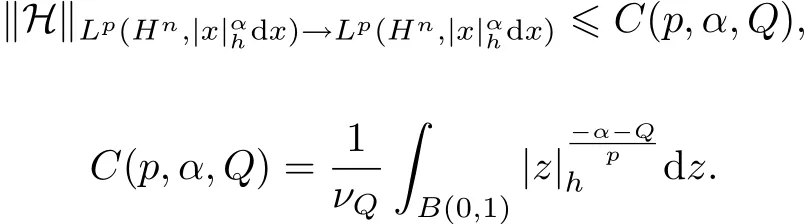
另一方面,令=1,取

即

则

因此,

综上,当ε→0+时,εε→1,并可得

因此,‖H‖Lp(Hn,|x|αhd x)→Lp(Hn,|x|αhd x)=C(p,α,Q)

(2)当p=∞时,只需令f(x)≡1即可获得结论.

(3)当p=1,0＜λ＜∞时,有

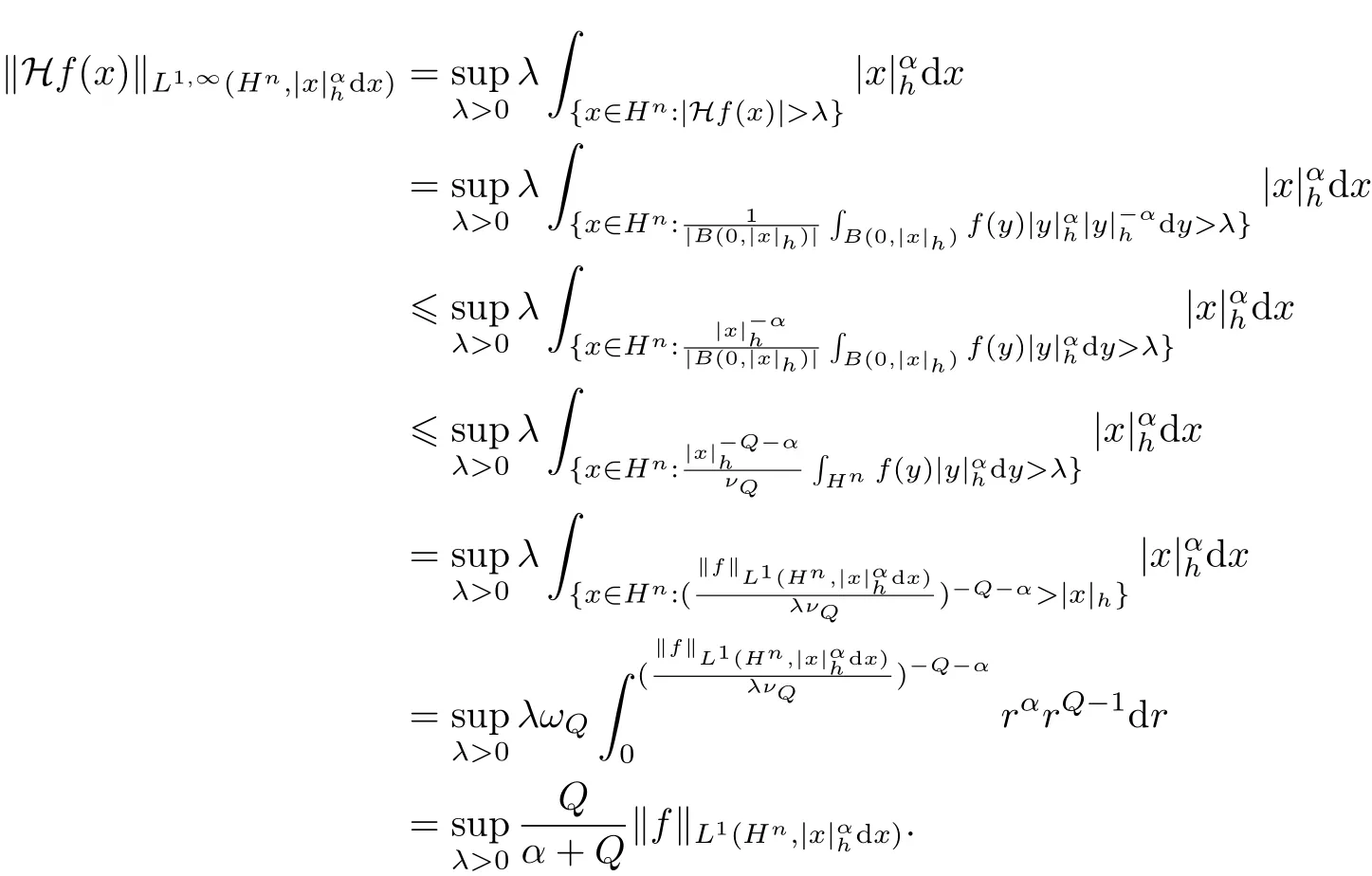
因此,

另一方面,取 f 1(x)= χB(0,1)(x),则 ‖f 1‖L1(Hn,|x|αhd x)=且

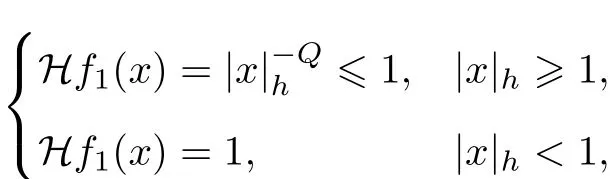
则

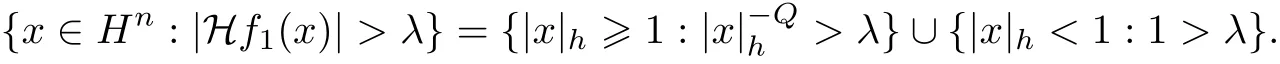
因此,

由 α ＜ 0,‖f 1‖L1(Hn,|x|αhd x)=,可得

因此,

推论1 当1＜p＜∞,α=0时,C(p,α,Q)=

这一推论与Wu等[8]的结论一致.