高频调幅交变电磁场中金属液滴悬浮振荡特性的数值模拟分析

朱宏达,雷作胜,郭加宏

自由液滴的振荡在液滴动力学中是一个重要的问题,对冶金、材料科学、天体物理等领域中相关问题的研究有重要意义[1-2].对液滴振荡规律的研究最早可以追溯到1879年,Rayleigh[3]基于线性近似理论推导了无黏性球形液滴小振幅振荡的频率方程,发现了液滴自由表面振荡和表面张力的关系.

在地面上研究自由液滴的振荡行为,需要克服液滴所受重力使其悬浮[4],目前主要采用超声悬浮法[5]和电磁悬浮法等.当金属液滴在交变电磁场中悬浮时,洛伦兹力、表面张力和重力的共同作用,使得金属液滴自由表面形状发生变化,并产生内部流动[6].El-Kaddah等[7]从电磁场、流场及温度场3个方面分别推导了悬浮金属液滴的控制方程.Gagnoud等[8]研究了不同表面张力的金属液滴随感应线圈中的电流变化而发生的形态变化.Cummings等[9]引入了金属液滴表面函数,导出了磁场和流场的关系,分析了磁感应强度、频率和液滴这几种基础模态的关系.由于地球重力严重影响了悬浮液滴自由液面的振荡频率分布,Cummings等[9]从理论研究中发现在重力作用下,悬浮金属液滴自由表面振荡频率退化为3个或5个频率,频率的个数与悬浮线圈的形状有关.欧洲TEMPUS团队[10]将实验设备发射到太空中,在微重力环境下,通过太空实验真实测量了金属试样在太空中悬浮熔化成液滴后的振动数据,并根据频谱测定了金属Au,Ni,Zr及NiNb等合金的表面张力.Egry等[11]根据Rayleigh公式和Cummings公式对比分析了地面和微重力条件下的振荡频谱异同对表面张力的影响.

已有很多学者开展了金属悬浮液滴振荡形态的数值模拟研究.Fujii等[12]计算了微重力下液态金属振荡频率和表面张力的变化关系.结果表明:当液滴呈球形时,频率谱只有一个波峰;当液滴形状扭曲时呈多个波峰,并呈现了在两种频率线圈叠加时悬浮液滴的形态.Pericleous等[13]数值模拟了冷坩埚悬浮熔炼钛铝合金在熔融后自由液面随时间的变化形状.Lei等[14]模拟了附着液滴在低频交变磁场下出现的模态振荡,发现其呈现出参数共振特征.

本研究根据高频调幅电磁场中金属液滴悬浮振荡的实验结果,构建了相应的二维轴对称数值计算模型,采用任意拉格朗日-欧拉(arbitrary Lagrangian-Eulerian,ALE)方法数值模拟了液滴自由表面的振荡.根据数值模拟结果,得到了高频调幅电磁场中悬浮振荡液滴的内部磁场、流场和自由表面形状.对液滴自由表面特征点的位移随时间的变化过程进行了傅里叶分析,获得了液滴在不同调制频率下的频谱,发现了高频调幅电磁场中金属液滴悬浮振荡的频谱特性.

1 电磁悬浮液滴数值模拟方法

1.1 控制方程及初、边值条件

高频调幅交变电磁场中液滴悬浮的磁流体动力学控制方程包括麦克斯韦方程组、洛伦兹力、流体动力学方程组.

(1)麦克斯韦方程组.

式中,E为电场强度(V/m),D为电位移矢量(C/m2),H为磁场强度(A/m),B为磁感应强度(Wb/m2),ρe为电荷密度(C/m3).B和D满足以下本构关系:

式中,µ0,µr为绝对磁导率和相对磁导率,∈0,∈r为绝对电容率和相对电容率.

在计算交变磁场时,为了简化电磁场方程,引入磁矢势A,满足

(2)洛伦兹力.

在电磁流体力学中,洛伦兹力是流体运动的外源力,根据欧姆定律

式中,σ为电导率,可以计算得到电磁场作用下液滴内部的洛伦兹力.

(3)流体动力学方程组.

连续性方程为

不可压流体N-S(Navier-Stokes)方程为

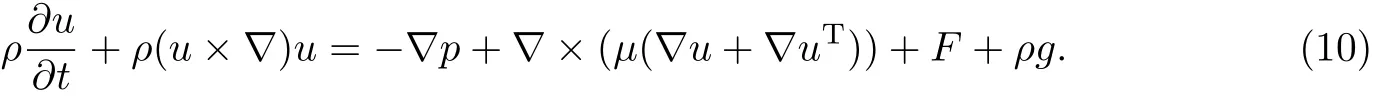
磁场和流场分布均考虑为周向均匀,并简化为二维轴对称流动,忽略液滴中金属液流动对磁场的影响.物理场的初、边值条件设定如下:在磁场计算时,设置计算域(空气域)边界条件n×A=0;在悬浮金属液滴流动模拟中,悬浮液滴初始为圆球形,流动速度为0,置于悬浮线圈和稳定线圈之间.

1.2 界面追踪和界面条件

振荡液滴自由液面的追踪计算采用ALE方法.ALE方法是传统的拉格朗日方法和欧拉方法的一种组合,综合了拉格朗日方法和欧拉方法的优点.计算流场时采用两相流计算模型,分别设置气态域和液态域,并划分自由移动网格.初始形状计算采用Winslow光滑法.在气态域和液态域界面上设置界面张力γ,约束液滴界面运动.移动网格在界面上跟随液态域流体网格一起移动.

(1)液滴和空气界面的压力为大气压p0=101 kPa.

(2)液滴表面张力为γ,液滴和空气界面满足

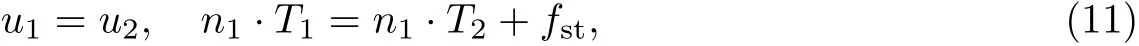
式中,u1,u2为两种介质的界面速度,T1,T2为两种介质的应力张量,fst为表面张力应力张量.

2 数值模拟结果

本研究数值模拟了高频调幅电磁场中金属液滴悬浮振荡过程.高频调幅交变电磁场由图1所示的线圈产生.该线圈与实验采用的线圈相同,采用螺线管形式,线圈正向绕制5匝,反向绕制2匝,分别起悬浮和稳定作用.线圈通入高频调制电流,高频频率fm=20 kHz,低频频率fc=1∼18 Hz,η为调制深度,电流调制模式为I(t)=I0(1+ηcos(ω2t))cos(ω1t),0＜η＜1,其中ω1=2πfm,ω2=2πfc,在线圈内产生高频调幅交变电磁场.

图1 实验和数值模拟采用的线圈Fig.1 Coil used in the experiment and numerical simulation

计算采用的液滴为纯铝液滴,初始时是直径为25 mm的球形.在线圈的磁场作用下液滴产生上下方向振荡.根据Rayleigh公式,球形自由液滴的固有频率分别为n=2,f2=5.93 Hz;n=3,f3=11.48 Hz;n=4,f4=17.78 Hz.

图2给出了调制深度η=0.3,调制频率为5.4 Hz,悬浮液滴在距离振荡最高位置8.59 mm处时,磁场和流场的计算结果.由图2(a)可见,液滴外部磁力线在液滴表面处与表面平行.液滴内磁场强度H只在液滴表面以下很薄的一层内有一定的数值,在液滴内部几乎为0.高频磁场中金属的集肤效应明显,因此金属液滴受到的洛伦兹力基本集中在表面附近.由图2(b)可见,液滴内部的流动呈现双涡结构.图3给出了实验中悬浮振荡液滴的形态,发现与数值模拟结果定性一致.

为进一步分析液滴在高频调幅电磁场中的振荡行为机理,对上述双频电磁场中液滴所受的电磁力进行了分析[15].根据麦克斯韦方程组,引入电磁势A(r,z,t),则磁场的表达式为

磁矢势A满足电磁感应方程:

若忽略欧姆定律中的感生电流项u×B,则单电流密度的角向分量j可以表示为

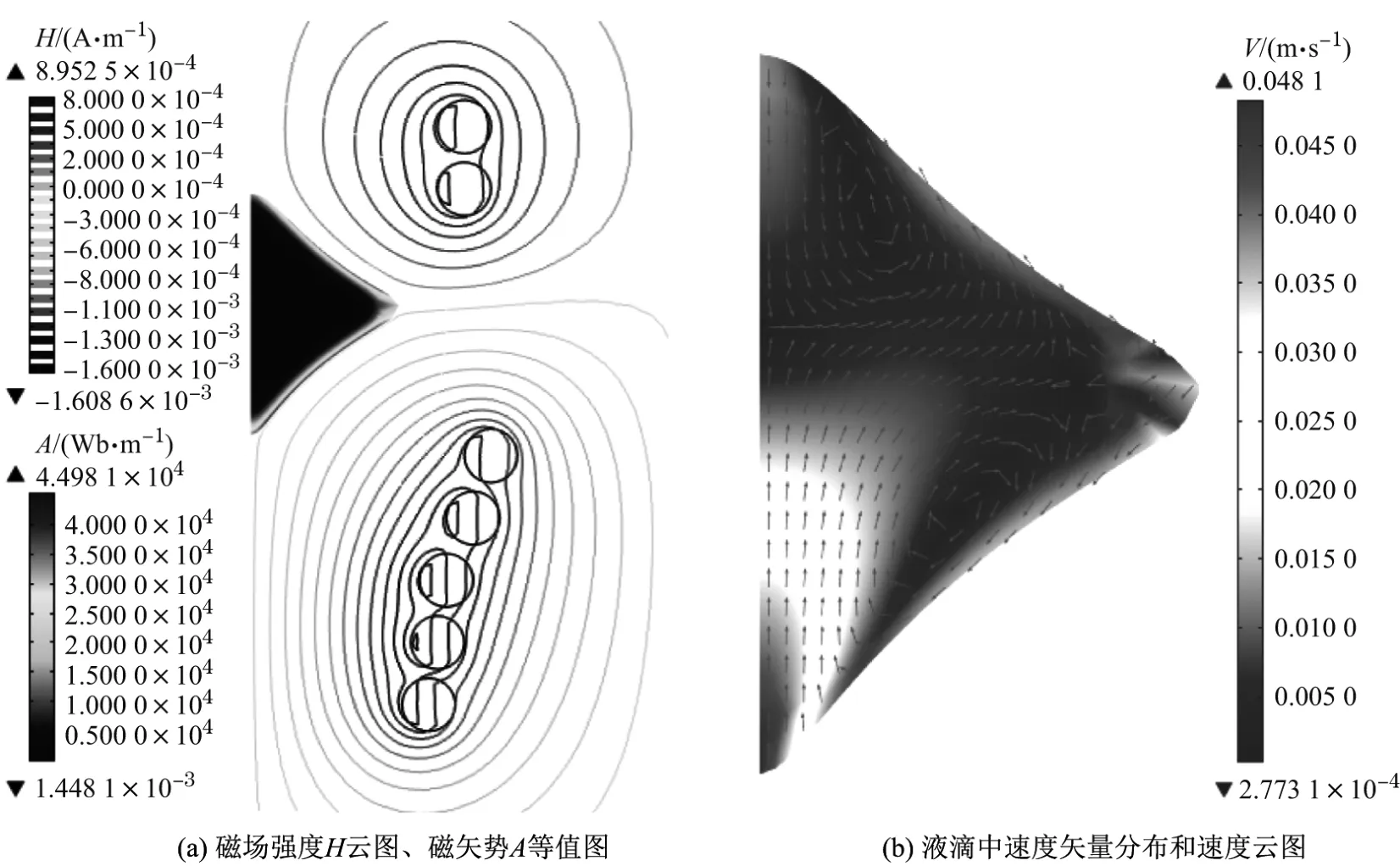
图2 磁场强度H云图、磁矢势A等值图、流场速度矢量分布和速度云图Fig.2 Distributions of magnetic fi eld intensity H,magnetic vector potential A,velocity vector and values

图3 当调制频率为5.4 Hz时,本实验测得的振荡液滴形状Fig.3 Form of the oscillating droplet obtained in the experiment when the modulation frequency is 5.4 Hz

根据式(12)和(14),可以得到相应的瞬时电磁力的表达式为

当调制形式为I(t)=I0(1+ηcos(ω2t))cos(ω1t)时,A=A0(1+ηcos(ω2t)),且在高频远大于低频的情况下,电磁力也不同于单频磁场作用下的电磁力.电磁力由高频时均电磁力F0和瞬变振荡力两部分组成,其形式为

式中,m20=1+,(t)=2αcos(ω2t)+cos(2ω2t).从以上公式可以得出高频调幅电磁场下的电磁力主要由两部分组成,其中振荡部分是基于低频的瞬变力,并包含有两种频率,即低频ω2和其倍频2ω2的瞬变力.

本研究模拟计算了不同调制频率的高频调幅电磁场中液滴的振荡过程.图4给出了调制频率分别为4.4,5.4和18.0Hz时,液滴顶部位移随时间变化的曲线以及相应的频谱图.可以看出,位移波形出现了一种周期性的双峰波形.通过傅里叶变换计算得到的频谱可以发现,悬浮液滴的振动响应频率主要有4个,其中主响应频率与调制频率一致,次响应频率正好是调制频率的倍频.这种频谱上的倍频关系与Perrier等[15]的理论分析结果相一致,但还存在更高倍频的振动.这是液滴在高频调幅电磁场中产生参数共振的结果.当调制频率设置为18.0 Hz时,频谱图上同样出现了倍频频率,在低频处也出现了其他频率.当调制频率越大时,高频调幅电磁场中倍频电磁力的影响就越小,而且会在低频附近出现其他频率.这些频率可能是由于液滴的平移运动造成的.

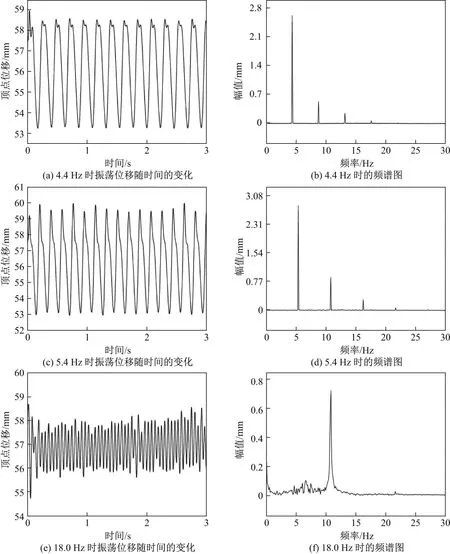
图4 4.4,5.4,18.0 Hz时液滴顶部振荡位移随时间变化的曲线及对应的频谱分析结果Fig.4 Displacement of the top point of the oscillating drop over time and its frequency spectrums when the modulated frequency is 4.4,5.4,18.0 Hz

3 结束语

本研究通过数值模拟得到了高频调幅电磁场中悬浮振荡液滴的内部磁场、流场和自由表面形状.对液滴自由表面特征点的位移随时间的变化过程进行了傅里叶分析,得到了高频调幅电磁场中金属液滴悬浮振荡的频谱特性.数值模拟结果与实验结果和理论分析结果定性吻合.

通过比较模拟结果和实验结果,发现液滴的数值模拟振荡形态与实验结果一致.数值模拟结果揭示高频调幅电磁场中悬浮振荡液滴内部存在双涡旋结构.对液滴自由表面特征点的位移随时间的变化过程进行傅里叶分析,分析了液滴在不同调制频率的交变电磁场中振荡的频谱.结果显示,液滴在高频调幅电磁场激励下产生了包含双频模式的振荡,这与理论上对双频电磁场的分析相一致.但还存在更高倍频的振动,这是液滴在高频调幅电磁场中产生参数共振的结果.