ORB特征四叉树均匀分布算法

刘宏伟，余辉亮，梁艳阳

(西南科技大学特殊环境机器人技术四川省重点试验室，四川 绵阳 621010)

0 引言

近年来，计算机视觉领域中，尺度不变特征变换(scale-invariant feature transform，SIFT)算法和加速鲁棒性特征(speeded up robust features，SURF)算法涌现。这2种算法在图像配准中的应用引起了众多学者的关注[1-6]，并取得了较好的效果。但这2种算法都要求建立高维描述符，需要大量的内存空间和较长的运行时间。王峰等人针对这个问题，提出了一种自适应控制SIFT特征均匀分布的算法[3]。该算法虽然有效地保证了特征点区分性和稳定性，但是耗时较长。针对这个问题，张云生等[1]人提出了基于改进加速旋转不变性特征提取(oriented fast and rotated brief,ORB)算法的遥感图像自动配准方法，虽然大幅度提升了配准效率，但是配准精度并不理想。其原因在于该算法是使用传统ORB特征提取的，即Rublee E等[2]人提出的ORB算法。该算法虽然在速度上相对于SIFT和SURF算法有了大幅度提升，但是精度相对较差。

1 Qtree_ORB算法框架

针对上述情况，本文提出了Qtree_ORB算法。该方法通过构建高斯图像金字塔[7]，对每层图像进行八叉树网格划分[8]，进而进行FAST角点检测，对较难提取的网格进行降阈值再检测，实现FAST角点的自适应提取。根据角点进行四叉树划分[9]，设计迭代算法计算节点。然后根据关键点的响应度[10]，筛选出每个节点中最好的关键点，从而大幅度降低冗余角点数。融合四叉树的思想，将特征点以四叉树的方式存储，这样可以有效剔除冗余重叠的特征点，使特征点均匀地覆盖到整个图像。Qtree_ORB算法框图如图1所示。

2 FAST角点自适应提取

结合FAST[11]算法和Brief[12]算法，ORB算法给FAST特征点增加了方向性，使特征点具有旋转不变性。同时提出了构建图像金字塔的方法，解决了尺度不变性。为了保证对每层图像金字塔FAST角点的提取精度，本文提出对构建图像金子塔中的每层图像金字塔进行八叉树网格划分，对划分网格作FAST自适应提取。

在构建八叉树网格过程中，设定初始化阈值iniThFast，进行角点提取。当设定iniThFast=25时，效果比较理想，判定此时网格区域提取的角点是否为空。如果为空，则设定miniThFast=7效果比较理想；否则按初始化阈值进行FAST角点提取。

width和height分别为图像的宽和高，i、j分别是行数和列数、Cols，Rows表示行分割数和列分割数，Chllw、Cellh表示行元和列元。每个网格范围为(Yini,Ymax)～(Xini,Ymax)。参数初始化，设置网格个数w=30,根据网格个数推导出行分割数Cols=width/w，列分割数Rows=height/w，间接推导出行元Cellw=width/Cols,列元Cellh=height/Rows。

网格行限定：

Yini=i×Cellw

(1)

Ymax=Cellw+6

(2)

网格列限定：

Xini=i×Cellh

(3)

Xmax=Cellh+6

(4)

FAST角点自适应提取迭代流程如图2所示。

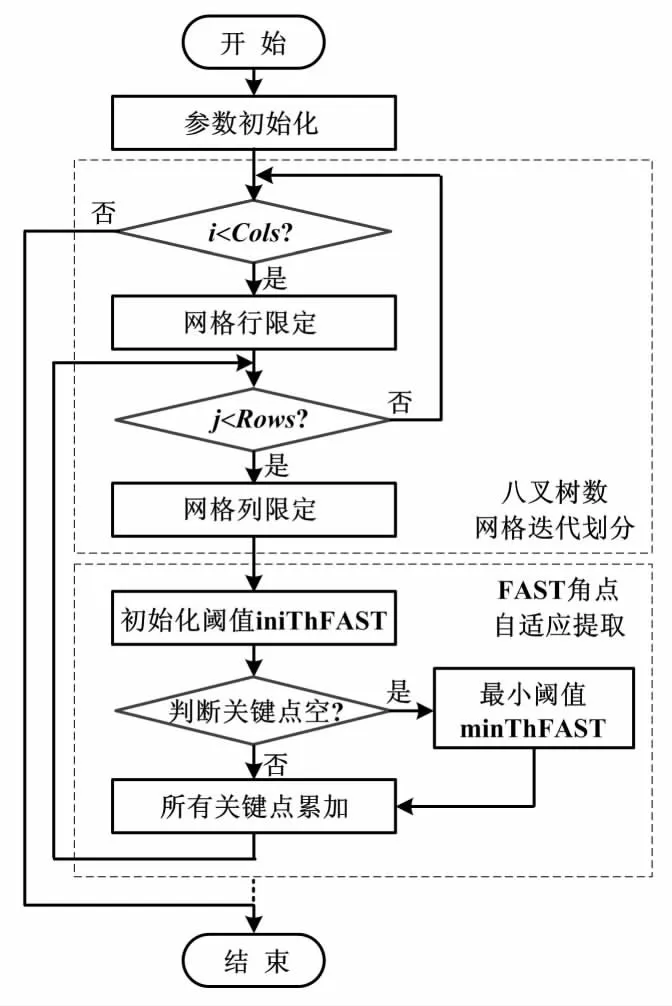
图2 FAST角点自适应提取迭代流程图Fig.2 Flowchart of FAST corner adaptive extraction iteration

3 角点四叉树处理

上述方法得到的角点存在特征点冗余，需要对角点四叉树进行进一步处理。四叉树的基本思想是二维空间数据递归划分为不同层次的树结构。运用这种思想，对图像中提取的角点进行四叉树划分。首先进行初始化节点计算，令初始化节点(父节点)为1，得到初始的四叉树结构，用四个象限表示(UL,UR,BL,BR)，如图3所示。将角点映射到初始的四叉树中，显然在初始化节点中角点个数不为1。

在此基础上，生成四个子节点n1、n2、n3、n4，根据角点位置映射到子节点中。映射以下规则。

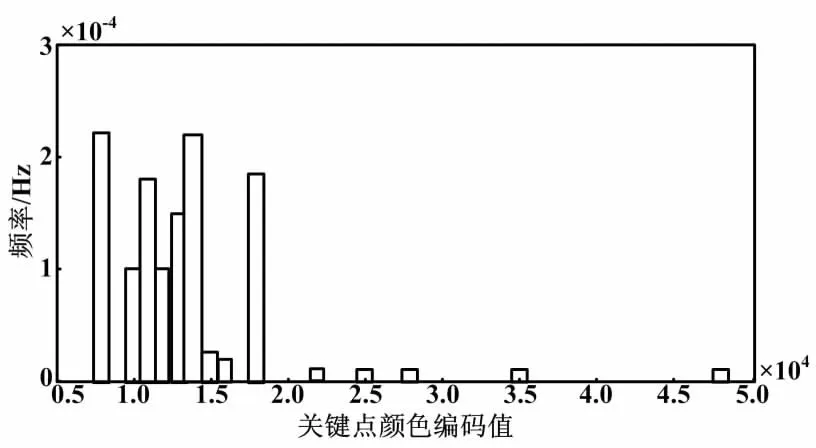
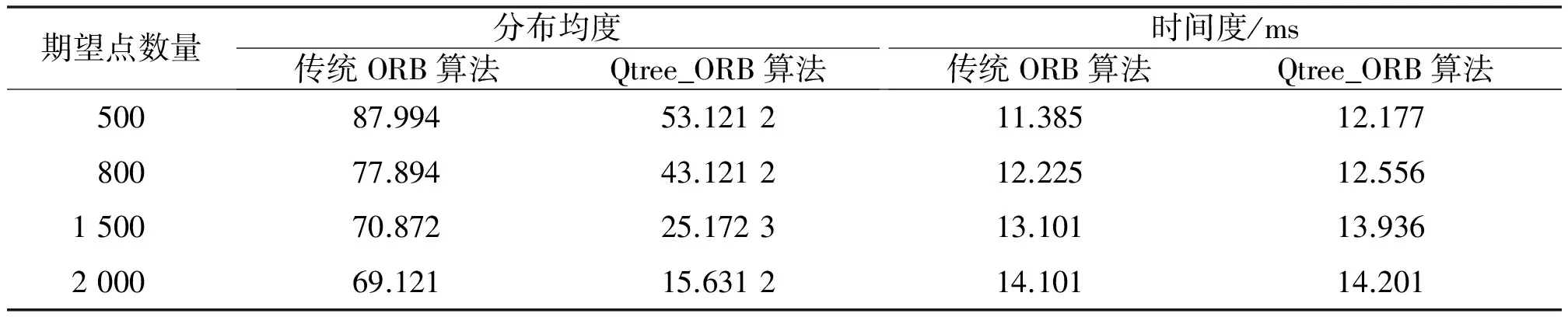
①如果角点位置PTkp满足条件PTkpx

②判断节点n1、n2、n3、n4内角点数量是否为1，如果等于1，不再生成子节点，否则继续生成子节点，继续步骤①。

当生成节点数大于期望特征数，或者节点个数不再增加时，则角点四叉数处理完成。

图3 初始化节点图Fig.3 Expression of initialization node

4 角点剔除

SURF中利用非极大值抑制(non maximum suppression,NMS)[10]来确定特征点的位置。关键点强度直方图如图4所示。

图4 关键点强度直方图Fig.4 Histogram of key point intensity

从图4可以看出，关键点响应强度越强，表示该点越鲁棒。当节点内角点数量不为1时，根据关键点响应强度，选取响应度最大的关键点，剔除响应度较小的点，这时节点个数等于特征数。

以上是对某一层金字塔图像进行上Qtree_ORB处理。为了保证尺度不变性，继续对其他的层图像进行相同处理即可。在此说明，得到的特征点的个数为8层高斯金子塔图像经过Qtree_ORB处理的节点个数总和。关于特征的主方向[4]，特征的描述子[4]计算与传统的ORB算法类似，这里不再介绍。

5 试验及结果分析

选用OpenCV 开源库，版本2.4.9，其中的ORB算子以及描述子作为传统ORB算子。为了保证试验的合理性，令Qtree_ORB也具有相同的功能，在相同硬件平台下，测试两种算子的特征分布情况以及时间度情况，并对试验结果进行分析。

选用一台CPU为i5-6500，运行内存4 GB的计算机，分别提取Qtree_ORB与传统ORB算子特征点，然后通过改变期望点的个数，观察关键点的分布情况。

为了更好地反映两种算法的特征分布情况，采用基于区域统计信息计算分布均匀度T。分布均度、时间度比较如表1所示。

从表1可以看出，随着期望点的增加，两种算法的分布均匀度都逐渐减小，其中Qtree_ORB减小得更加明显且分布均匀度更小，说明特征分布质量越好。针对小分辨率图像，在时间度的对比中，发现Qtree_ORB算法与传统的ORB算法时间度差别并不是很大。由于是在ORB算法的基础之上进行特征点空间改进，这在耗时方面有一定的增加。

表1 分布均度、时间度比较Tab.1 Comparison of distribution uniformity and time degree

6 结束语

针对传统ORB算法存在的特征提取分布不均匀，重叠特征点较多等问题，提出了Qtree_ORB算法，并对整个算法进行设计。通过试验，验证了Qtree_ORB算法能使特征分布更加均匀，并可同时保持计算的高效性。Qtree_ORB算法的不足之处是当期望点为2 000

时，特征重叠情况加重。同时在超分辨率图像中，并没有进行时间度的比较，可能耗时会更长，希望在以后工作中进行改进。

参考文献:

[1] 张云生,邹峥嵘.基于改进ORB算法的遥感图像自动配准方法[J].国土资源遥感,2013,25(3):20-24.

[2] RUBLEE E,RABAUD V,KONOLIGE K,et al.ORB:An efficient alternative to SIFT or SURF[C]// IEEE International Conference on Computer Vision.IEEE,2011:2564-2571.

[3] 王峰,尤红建,傅兴玉.应用于SAR图像配准的自适应SIFT特征均匀分布算法[J].武汉大学学报(信息科学版),2015,40(2):159-163.

[4] 王姮,王曼,张华,等.基于PCA模式和颜色特征的钢轨表面缺陷视觉显著性检测[J].自动化仪表,2017,38(1):73-76.

[5] RUBLEE E,RABAUD V,KONOLIGE K,et al.ORB:An efficient alternative to SIFT or SURF[C]// International Conference on Computer Vision.IEEE Computer Society,2011:2564-2571.

[6] LINDEBERG T. Scale invariant feature transform[J].Scholarpedia,2012,7(5):2012 - 2021.

[7] 屈玉福,刘子悦,江云秋,等.自适应变尺度特征点提取方法[J].光学精密工程,2017,25(1):188-197.

[8] 冯泽邦.一种基于平面八叉树的森林小班林火蔓延模拟方法:CN 102799703 A[P].2012.

[9] AREFIN M A,UDDIN M Y S,GUPTA I,et al.Q-Tree:A multi-attribute based range query solution for tele-immersive framework[C]//IEEE International Conference on Distributed Computing Systems.DBLP,2009:299-307.

[10]BAY H,TUYTELAARS T,Gool L V.SURF:Speeded up robust features[J].Computer Vision & Image Understanding,2006,110(3):404-417.

[11]CALONDER M,LEPETIT V,STRECHA C,et al.BRIEF:Binary robust independent elementary features[C]//European Conference on Computer Vision.Springer-Verlag,2010:778-792.

[12]朱海峰,赵春晖.图像特征点分布均匀性的评价方法[J].大庆师范学院学报,2010,30(3):9-12.