燃烧空燃比控制系统性能评估

李奇达，谭树彬

(1.东北大学信息科学与工程学院，辽宁 沈阳 110819；2.东北大学流程工业综合自动化国家重点实验室，辽宁 沈阳 110819)

0 引言

在实际工业过程中，由于系统长时间的运行导致零件的磨损和故障，系统特性的变化等因素造成控制系统性能下降,这使得产品质量也随之下降。如今，控制器性能监控与评估是热点研究方向之一。早在20世纪六七十年代，Astrom、DeVries和Wu等人就已经开始了控制器性能监控与评估工作。如今，研究方向主要集中在：基于最小方差控制性能评估方法的推广和完善；基于广义最小方差的性能评估基准；基于诊断方法的性能评估基准[1]。基于主元分析(principal component analysis，PCA)与最小二乘支持向量机(least squares support vector machine，LSSVM)相结合的方法，大多应用在多变量控制系统[2]。

本文以燃烧空燃比控制系统为研究对象，对其进行控制性能评估，实现了系统的实时监测，大幅度提高了控制器性能。

1 燃烧空燃比系统参数辨识

1.1 燃烧空燃比系统结构

燃烧空燃比系统是一个单闭环系统，其系统结构如图1所示。

图1 系统结构图Fig.1 Structure of the system

图1中：X1(s)为温度设定值；W1(s)为温度控制器传递函数；Wv1(s)为执行器(燃气调节阀传递函数)；K为空气调节阀与燃气调节阀变化比例；Wo1(s)为燃气调节阀开度到燃气流量的传递函数；Wo2(s)为空气调节阀开度到空气流量的传递函数；Wot(s)为温度被控对象；Q1为燃气流量；Q2为空气流量；F(s)为烟气含氧量计算模型；Wmt(s)为温度测量变送环节；Y1(s)为燃烧室温度。

燃烧空燃比控制系统可以近似成一个单输入单输出系统。其模型主要可以分为两大部分。第一部分为气路，气路部分又分为进气压力模型、节气门处空气质量流量模型以及进气管处空气质量流量模型；第二部分为油路，油路部分由燃油蒸发子模型构成[3]。

空燃比控制的目的是使燃气与空气的配比达到最佳，然而燃料与空气调节回路响应速度不一，燃料热值波动、烧嘴特性差异以及燃烧负荷发生变化都无法保持最佳配比[4]。

为了提高燃烧效率，需要对控制器进行性能评价，从而保证系统一直高效工作。

1.2 系统参数辨识

经过公式推导，可得式(1):

(1)

1.3 系统参数辨识仿真

对燃烧空燃比系统求闭环传递函数，从而求出系统的差分方程。为了验证所提方法的有效性，假设系统的差分方程为：

z(k)+a1z(k-1)+a2z(k-2)=

b1u(k-1)+b2u(k-2)+V(k)

式中：a1=1.5;a2=0.7;b1=1.0;b2=0.5;V(k)为噪声信号。

递推最小二乘辨识系统参数仿真如图2所示。

图2 系统参数仿真图Fig.2 Simulation of system parameters

2 控制系统性能评估

2.1 基于线性回归算法

Damien Uduehi等人在2006年提出了一种线性回归的算法，利用闭环回路数据进行控制器性能评估。这种方法避免了求解丢番图方程，使得运算更加简单。

系统控制性能评估指标为：

(2)

2.2 基于改进线性回归算法

线性回归算法具有以下缺点。

①每次数据处理量大，占用内存多，而且无法实现实时估计。

②在实际工业过程中，大部分系统为扰动时变系统，使得历史数据不再有意义。

③随着数据增长，会产生数据饱和的现象。

本文提出基于遗忘因子的线性回归算法。该算法不仅能够改善原始线性回归算法由于计算数据量大导致数据饱和的特点，而且能够增加数据的有效性、提高数据的信息量，避免了由于时变系统参数的变化而导致的输出方差不准确现象[5]。

①遗忘因子的定义。

距离k步的两个数据，其衰减比为βk。β为遗忘因子，β∈(0,1]。

②基于遗忘因子的线性回归算法。

引入遗忘因子后，系统输出数据乘上遗忘因子即可得出系统控制性能评估指标，如式(3)所示。

(3)

③遗忘因子的选择。

当β=0.99、采样数据为100时，衰减比为0.366,采样数据为400。为了保证数据的有效性，防止数据发生饱和，需选取合适的β。本节令β=0.999，则衰减比为0.670。

基于遗忘因子的线性回归算法基本步骤如下。

①通过相关性分析法来计算时延d；

④计算系统控制性能指标。

2.3 燃烧空燃比系统仿真

燃烧空燃比系统框图如图3所示。扰动为有色噪声，输入为正负1随机信号。两种评价方法对燃烧空燃比系统控制性能评价结果对比如图4所示。

图3 燃烧空燃比系统框图Fig.3 Block diagram of combustion air-fuel ratio system

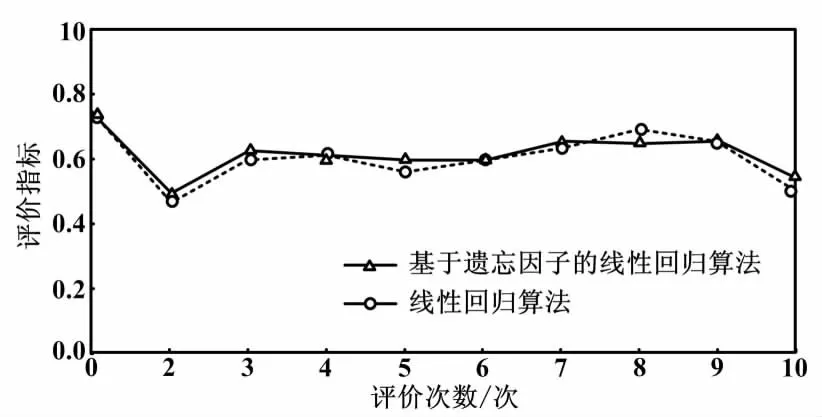
图4 空燃比系统性能评价对比图Fig.4 Comparison of performance evaluation of air-fuel ratio system

3 多扰动空燃比控制系统

3.1 空燃比系统扰动分析

系统具有多个扰动动态时，为了对多扰动系统进行控制器性能评估，可以对每个扰动设置相应的权值[6]。本文提出了H2范数和设置权重相结合的方法。为了保证控制系统在扰动参数变化时，能够继续对其有控制作用，即保证系统有较好的鲁棒性，可对GN求H2范数，得：

(4)

由Parseval定理可得，式(4)值越小，证明PID控制器控制效果越好。通过对式(4)求最小值，得出控制器最佳性能指标。

(5)

则当前PID控制器的性能评估指标为：

(6)

式中：(||GNi||)actual为实际值。

yt=Gq-dut+Nat

(7)

则：

(8)

式中：G为过程传递函数；N为扰动传递函数；ut为PID控制器输出；yt为系统输出；k为控制器参数at是均值为0、方差为1的白噪声，当系统具有多个扰动动态时，将其设为Niait。

根据每个输出的重要程度，将每个扰动分别乘上一个权重系数λ1,λ2,…,λn,从而得出系统性能函数。

(9)

可对式(9)求最小值，得到:

(10)

式中：(Jtotal)ideal为控制器综合性能最优值;k1、k2、k3为控制器最佳参数。

将理想控制器作用下的被控变量的输出方差作为一个基准，将实际多变量控制器作用下的被控变量的输出方差与基准进行比值运算[7]。对式(10)求最小值，求出PID参数。控制器综合性能评估指标如式(11)所示：

(11)

3.2 系统性能评价仿真

基于最小方差基准,自相关性分析法在检测系统振荡特性中具有重要意义[8]。控制阀的黏滞特性容易诱发控制回路产生振荡现象，从而导致生产过程效率降低，甚至生产停止[9]。为了有效解决此类现象，假设燃烧空燃比系统有两种扰动动态，分别为管压力波动和阀门黏滞。

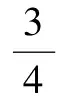
管压力波动、阀门黏滞的扰动如图5所示。当前控制器对管压力的波动、阀门黏滞的抑制效果如图6所示。

图5 扰动图Fig.5 Disturbances

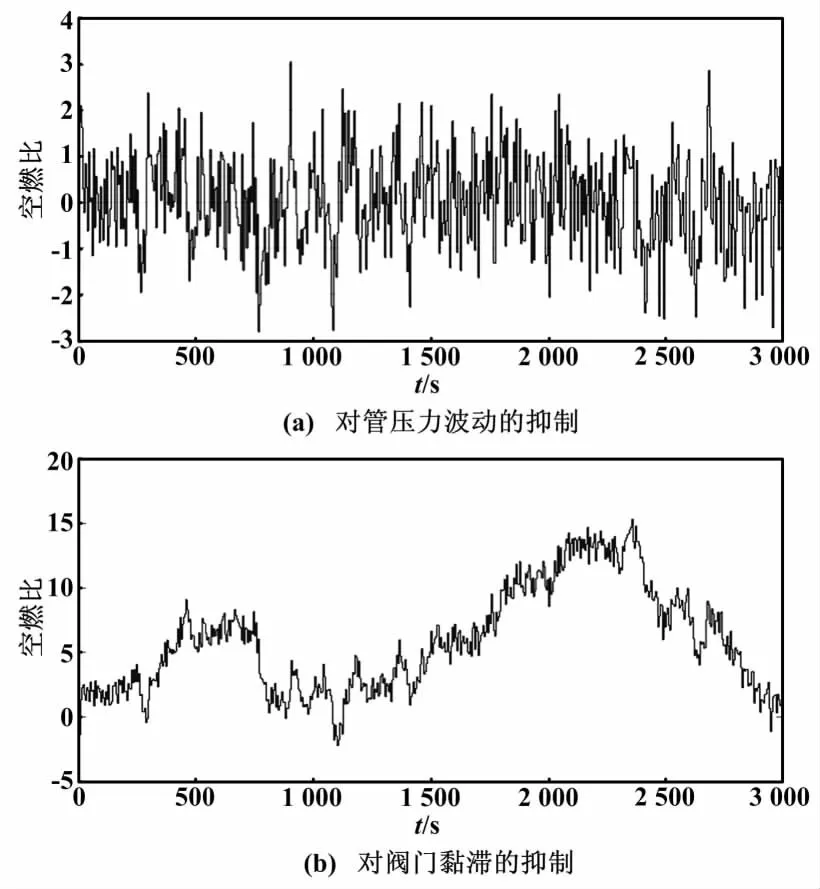
图6 当前控制器对扰动抑制效果图Fig.6 Inhibitory effects of current controller on disturbances

图7 最优PI控制器对扰动的抑制效果图Fig.7 Inhibitory effects of the optimal PI controller on disturbances

随着时间的推移，系统的参数可能会发生变化，导致系统输出方差增加、控制系统性能下降[10]。而控制器决定输出方差的大小，选择合适的参数对于系统性能的提升至关重要[11]。根据以上评价指标，可实时获得最优PI控制器参数。

4 结束语

采用线性回归算法和遗传算法两种方案对燃烧空燃比系统进行了性能评估并对比分析，实现了对系统的实时监测。针对多扰动燃烧空燃比系统，提出了H2范数和权重系数相结合的方法。对系统管压力的波动和阀门的黏滞这两种扰动进行了综合控制器性能评估，设计了最优控制器，有效解决了由于阀门黏滞导致系统振荡的问题。

参考文献:

[1] 徐展.PID控制器性能评估[D].保定：华北电力大学，2010.

[2] 蔡宏斌,苏成利.PCA-LSSVM方法的控制系统性能评估[J].自动化仪表,2014,35(1):10-14.

[3] 李佳怡.基于最小方差算法对空燃比回路的性能评估[D].吉林：吉林大学，2011.

[4] 陈友文,柴天佑.蓄热式加热炉的空燃比控制[J].控制工程,2011,18(5):703-706.

[5] 陈绍绵.工业过程的控制、监测与诊断研究[D].杭州：浙江大学,2010.

[6] ZHANG D F.Improved LQG Benchmark based control performance monitoring for multivariable systems [C]//25th Chinese Control and Decision Conference，2013：4353-4358.

[7] 刘春平,王昕,王振雷.基于MMTMV方法的多变量时变扰动系统性能评估[J].自动化学报,2015,41(5):928-935.

[8] 郭建文.基于改进广义最小方差基准的串级控制系统性能评估[D].上海：华东理工大学,2013.

[9] 王挺任.控制阀黏滞特性补偿控制方法研究[D].杭州：浙江大学,2016.

[10]张巍,王昕,王振雷.基于多模型混合最小方差控制的时变扰动控制系统性能评估[J].自动化学报,2014,40(9):2037-2044.

[11]牛玉广,谷佳琪,孟庆伟.工业过程PI控制器性能评价[J].化工自动化及仪表,2013,40(6):730-733.