框架式浮鱼礁波浪水动力特性数值模拟研究

张 健， 潘 昀， 冯德军， 桂福坤

(浙江海洋大学，国家海洋设施养殖工程技术研究中心,浙江 舟山 316002)

由于过度捕捞和海洋污染，渔场遭到破坏，保护和修复海洋渔场势在必行。人工鱼礁是用来改善海洋生态环境、建设海洋牧场的人工设施，能为海洋生物提供繁殖、生长、栖息的场所，同时复杂多变的空间更能为鱼类提供躲避区[1-4]。人工鱼礁投放后，周围海域的流、光、音、底质等非生物环境会发生变化。这种变化又会引起生物环境的变化，增大生物量，从而形成良好的渔场或增养殖场，集鱼效果也非常明显[5]。由于沉式鱼礁具有投放简单、成本低、材料来源广、集鱼效果显著等优点，目前国内应用很广。然而，沉式鱼礁在黏土、淤泥以及沙质海区可能会导致礁体整体下沉，过多的淤泥还会覆盖甚至掩埋着生在礁体上的生物，降低含氧量，阻碍光线，影响鱼礁功能[6]。由于长江携带大量悬浮泥沙，使舟山海域附近海底大量淤泥堆积，因此，沉式鱼礁并不适合舟山海域，而浮鱼礁则能很好地解决这个问题。

浮鱼礁是继沉式鱼礁之后的一种海洋增养殖设施，主要是为诱集中上层鱼类而设计。浮鱼礁的作用范围和机理与沉式鱼礁不同，主要是由锚块、锚绳和浮体组成，有些浮鱼礁还会配有浮球[7]。浮鱼礁根据作用区域不同，可分为表层、中层、底层和深海等。表层和中层浮鱼礁分别作用在水深10 m和20～50 m附近海域。日本在浮鱼礁的研究应用上处于世界领先地位，拥有适用于大水深和全水层的浮鱼礁，且已投入应用，并取得了很好的效果。如：礁体位置为海面的表层浮鱼礁，礁体位置为海面以下 20 m的中层浮鱼礁，整体高度90 m左右、应用于大水深海域的深海浮鱼礁[8]。国内对浮鱼礁的研究较少，余求妹等[9]设计探讨了浮绳式网箱人工浮鱼礁，张丽珍等[10]设计了近海中上层浮鱼礁，实际投放于象山港海洋牧场，结果表明浮鱼礁能较快地吸引鱼类。在实际应用中，浮鱼礁通常投放在≥10 m水深海域[8]。受到天气和潮差影响，海水波高和水深变化会导致锚泊系统和礁体位移产生变化[11]。浮鱼礁不是单一地投放，在投放人工浮鱼礁时，要注意与其他用途的海洋区域有足够的距离，避免由于礁体的移动而影响海域的其他功能[12]。因此，在确保浮鱼礁系统安全的前提下，当波高和水深发生变化时，利用数值模拟的方法，研究框架式浮鱼礁的水动力特性，计算锚绳受力大小和礁体位移能为浮鱼礁实际投放间隔距离提供理论参考，计算锚泊系统受力情况能对锚绳材料选择争取利益最大化提供帮助。

1 框架式浮鱼礁结构参数

人工鱼礁主要有箱形礁体、框架形礁体、三角形礁体、梯形礁体和异形礁体等[13]。为便于比较，定义ε和η为优化参数，ε为礁体空方体积与礁体体积之比，η为礁体表面积与礁体体积之比，对于增值附着类海洋生物礁体，其η值要高些，若是以诱集鱼类为目的，其ε值应高些[8]。为保证浮鱼礁具有良好的集鱼效果，设计时通常要遵循的基本原则：较大的礁体表面积、良好的透空性、充分的透水性以及切实的可行性。本文选择框架形礁体为研究对象。鱼礁由框架浮体(图1中12条高密度聚乙烯(HDPE)管道棱边热熔焊接而成的空心框架)和锚绳两部分组成，具体尺寸见表1。框架浮体尺寸为0.4 m×0.4 m×1 m(长×宽×高)，管道直径0.05 m，浮体密度400 kg/m3。锚绳原长5 m，直径0.01 m，锚绳密度950 kg/m3。采用耐磨耐腐蚀的聚乙烯(PE)材质[14]。在框架浮体底端中点处系缚锚绳，锚绳锚碇点用重块沉到水底。

假设波浪作用下框架浮体始终不出水，并且波浪传播方向与框架浮体六面中的ABCD面平行，那么框架浮体的运动仅在波浪传播方向发生，即可视为二维刚体运动(图1)。那么，框架浮体运动可以简化为EFGH平面上的二维平动和转动，进而研究对象分离为框架浮体E’F’G’H’和锚绳之间的运动。

图1 框架式浮鱼礁的基本构成及坐标

项目材料尺寸/m直径/m密度/(kg/m3)拖曳力系数CD惯性力系数CM锚绳弹性系数C1锚绳弹性系数C2框架浮体HDPE0.4×0.4×1.00.054000.81.2——锚绳PE5.00.019500.61.2345.3×1061.0121

2 框架式浮鱼礁模型建立

波浪作用下框架浮体及其锚绳运动数值模拟方法主要采用有限单元法计算框架浮体的受力和绕质心的力矩，进而离散时间确定框架浮体的平动和转动，采用有限集中质量点法计算柔性锚绳的受力和形变后的拉力，同样离散时间确定锚绳集中质量点的运动速度和空间坐标。由于Fortran软件具有强大的计算能力，因此先用其进行数值模拟，计算框架浮体位移和受力情况，然后用Matlab软件对数据结果进行可视化处理。

2.1 框架浮体受力与运动

2.1.1 框架浮体受力

数模分析采用有限单元法[15-16]，根据已有文献将AB管道划分为10份即可满足模拟精度。由于BC管道只有AB管道的0.4倍，BC管道就被划分为4个单元，因此，框架浮体E’F’G’H’被划分为10×4个有限单元(高×长)。框架浮体单位受力主要包括重力、浮力、波浪力等，在系缚点(图1中P点)处计算锚绳拉力。采用线性波理论，根据波浪要素的弥散关系，求解波浪场的水质点速度(式1)和水质点加速度(式2)，再使用莫里森方程计算框架浮体受到的波浪力。

(1)

(2)

式中：VX—X轴水质点速度，m/s；VZ—Z轴水质点速度，m/s；aX—X轴水质点加速度，m/s2；aZ—Z轴水质点加速度，m/s2；H—波高，m；k—波数；x—水质点横坐标，m；z—水质点纵坐标，m；d—水深，m；ω—圆频率，rad/s；T—周期，s；t—步长，s。

框架浮体四边均为圆柱形杆件，因此具有圆柱的水动力性质，其水动力系数与水质点的相对运动速度方向有关[15-17]。在计算每个浮体单元波浪力时应考虑浮体与波浪入射方向的夹角。本文建立整体坐标系(X,Y,Z)，同时在浮体单元处建立局部坐标系(δ,η,τ)，τ方向为浮体单元方向，在计算τ方向时，会出现4个浮体单元方向，本文定义向上和向右为正方向。δ轴在τ方向和水质点相对速度VR组成的平面内与τ轴垂直，η轴与τ和δ轴方向组成的平面相垂直。

vR=v水-va

(3)

式中：vR—水质点与浮体单元的相对速度，m/s；v水—水质点速度，m/s；va—浮体单元速度，m/s。

在整体坐标下，局部坐标系的δ,η,τ轴单位矢量可以通过已知的水质点相对速度VR与浮体单元方向向量τ叉乘得到，为：

(4)

式中：eδ,eη和eτ分别为局部坐标系(δ,η,τ)3个轴的单位矢量坐标[15]。

因为在整体坐标系下只考虑X、Z两个方向的受力，所以直接通过向量运算建立浮体的受力公式，如式(5)所示。

(5)

式中：FD浮体、FI浮体—浮体单元受到的速度力和惯性力，N；FDη、FDτ—速度力FD浮体在局部坐标系上的分量；FIη、FIτ—惯性力FI浮体在局部坐标系上的分量。展开为式(6)和式(7)。

(6)

(7)

式中：ρw—水体密度，kg/m3；CD—局部坐标系的速度力项系数；Aη、Aτ—浮体单元在局部坐标系η和τ方向上的投影面积，m2；ψ—浮体单元体积，m3；CM—局部坐标系上的惯性力项系数。

在整体坐标系下将浮体各集中质量点所包含的受力进行累加，并将其分配到集中质量点上，然后利用牛顿第二定律建立质点运动方程，简化后的质点运动方程[15-17]为：

Ma=T+FD浮体+FI浮体+W+B

(8)

式中：M—集中质量点的质量，kg；a—各集中质量点的加速度矢量，m/s2；T—集中质量点所受到的张力矢量，N；W—质点的重力矢量，N；B—质点的浮力矢量，N。

2.1.2 框架浮体的平动与转动

本文中浮架的运动可以看作刚体运动，刚体运动一般包括平动和转动，这也说明牵连速度和牵连加速度包含平动和转动两部分。因此，根据刚体运动的速度和加速度合成原理，刚体任意点的运动速度(加速度)分别由牵连速度(加速度)、相对速度(加速度)和科氏速度(加速度)矢量合成，即：

(9)

式中：va—相对于固定坐标系的绝对速度，m/s；aa—相对于固定坐标系的绝对加速度，m/s2；ve、ae—牵连速度、牵连加速度，由坐标相对运动导致，m/s，m/s2；vr—刚体中点相对坐标系的相对速度，m/s；vk—科氏速度，对于刚体而言，其值为0；ar—刚体中点相对坐标系的相对加速度，m/s2，对于刚性浮架而言，相对速度和相对加速度为0；ak—科氏加速度，m/s2，是牵连运动和相对运动之间相互影响导致的，对于刚体而言同样为0。综上分析，刚体在固定坐标系(绝对坐标系)中的运动速度和加速度实际上就是牵连速度和牵连加速度，va=ve，aa=ae。

(1)计算平动。单考虑平动时，刚体无转动位移，计算公式为：

(10)

式中：r0—平动距离,m;ve1—平动部分牵连速度，m/s；ae1—平动部分牵连加速度，m/s2。

(2)计算转动。在分析刚体的转动时，当动坐标和固定坐标静止不重合时，刚体转动是对应固定坐标原点，实际上常取动坐标和固定坐标质心重合点。本文因为要考虑到锚绳和框架浮体之间的相互作用，刚体绕质心转动的角速度为ω，这一转动角速度实际上即为动坐标相对于固定坐标的牵连角速度[18]，即ωe=ω，由于转动存在，刚体中任意点的牵连速度都不一样，刚体中任意一点的牵连角速度为：

ve2=ωe×r

(11)

式中：r—对应点原点的矢径。至此可以得出整个刚体运动的绝对速度。

va=ve1+ve2

(12)

式中：ve2—刚体中的任意一点的牵连角速度，rad/s。

2.2 锚绳受力与运动

锚绳属于典型柔性结构物，也可以采用集中质量法进行模拟。假定锚绳由有限的无质量弹簧连接的集中质量点构成，通过计算集中质量点在动力边界条件作用下的偏移来获得锚绳的形状[15-17]。模型的集中质量点设于锚绳两端，每个集中质量点包含锚绳上下2个锚绳(图2)。

图2 锚绳节点示意图

在浅海条件下，锚绳集中质量点受力、计算波浪力方法与框架计算方法相同。在整体坐标系下将各集中质量点所包含锚绳的受力进行累加，并将其分配到集中质量点上，然后利用牛顿第二定律建立质点运动方程。锚绳模型简化后的质点运动方程[19-20]为：

(13)

式中：M—集中质量点的质量，kg;a—各集中质量点的加速度矢量，m/s2;L0—锚绳原始长度，m；L—变形后的长度，m；L0—锚绳原始长度,m;C1、C2为框架浮体的材料弹性系数;FD、FI—分别是锚绳单元受到的速度力和惯性力,N;ε—伸缩比；dm—锚绳直径，m。

3 结果与分析

研究了波高为1.5、2、2.5和3 m，水深为8、9、10、11和12 m，周期为2 s工况下，浮架水平方向最大偏移、最大偏转角度和锚绳最大受力。定义框架浮体E’F’管道为左构件，F’G’管道为下构件，G’H’管道为右构件，H’E’管道为上构件。为便于分析，本文在整体坐标系下，选取框架浮体上、中、下3个点为一组参数进行数据分析，其中上点为上构件中点坐标，中点(是一个虚拟的点)为框架浮体质心坐标，下点为下构件中点坐标。当只有波高变化时，初始状态锚绳长5 m，下端系缚在锚碇点，上端系缚在框架下点，此时框架上点距离水面2 m，水深8 m，波高变化不影响初始状态；当只有水深变化时，框架和锚绳初始状态同上，水深每增加1 m，系统初始状态纵坐标向下增加1 m。

3.1 波高对浮体最大偏移和最大转角的影响

在水深8 m，波高分别为1.5、2、2.5、3 m的工况下，框架浮体上中下3个点的运动轨迹如图3中a、b、c、d所示。可以看出，当波高3 m时浮体水平最大偏移出现在±0.3 m附近，当波高1.5 m时浮体水平最大偏移出现在±0.14 m附近，波高每增加0.5 m，浮体最大偏移相应增加约0.05 m，波高3 m的最大偏移量约为波高1.5 m时最大偏移量的2倍。相同工况下，正负方向最大转角随波高的变化如图4所示。

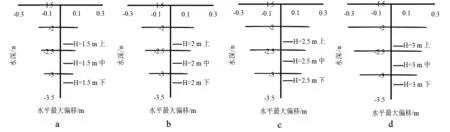
图3 水平最大偏移随波高变化情况

图4 正负方向最大转角随波高变化

定义沿波浪传播方向为正方向，与波浪传播方向相反为负方向。由图4可知，随着波高增加，浮体正负方向偏转角度增加，波高每增加0.5 m，正向最大转角增加1.2°，负向最大转角增加1.4°。

波高的变化对浮体正负向最大偏转角度的影响基本一致。当波高增大后，浮体最大偏移和正负方向最大偏转角度均增大，原因是波浪的水质点速度很大，导致水质点相对浮体的运动速度较大，浮体受波浪力随之增加，从而产生剧烈运动。图4中，X轴左右偏移量基本相等、正负偏转角度基本相等，说明在规则波浪作用下，框架式浮鱼礁的左右摇摆运动幅度基本保持一致。

3.2 水深对浮体最大偏移和最大转角的影响

波高3 m，水深分别为8、9、10、11、12 m时，框架浮体上中下3个点的运动轨迹以及最大转角随水深而变化，此时浮体最上端距离水面分别为2、3、4、5、6 m(图5)。定义框架浮体最上端(图1中E’H’中点位置)至静水面的距离与水深的比值为框架浮体的相对入水深度。图5表明，当相对入水深度为1/4时，框架浮体水平偏移最大，随着水深增加；从1/4至2/5变化时，浮体最大水平偏移迅速减小；从2/5至1/2变化时，浮体在水平方向几乎没有运动，这是由于随着水深的增加，水质点运动速度迅速减小，导致浮体受波浪力也迅速减小。

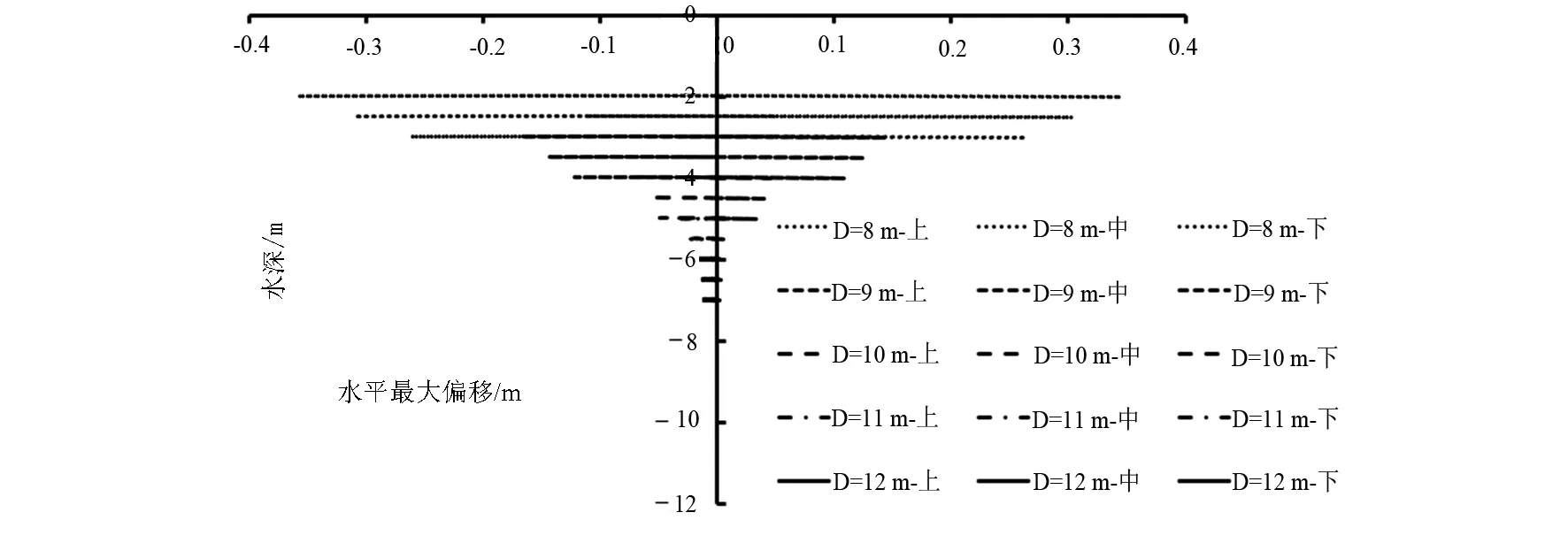
图5 最大偏移量随水深变化情况

相应地，图6所示，当相对入水深度从1/4至2/5变化时，浮体正负方向最大偏转角度迅速减小，当浮体从距离水面2/5到1/2变化时，浮体正向和负向的最大偏转角度变化趋于平缓；当到达1/2时，浮体正负方向最大偏转角度几乎没有变化。考虑到水深变化对浮体的偏移和偏转角度影响十分显著，而实际海洋中由于潮差的存在，相对入水深度会发生变化，因此在实际设计投放浮鱼礁时，应充分考虑涨落潮对浮鱼礁系统的相对入水深度、最大偏移量和浮体最大偏转角度的影响。综上，浮体上端至水面的距离与水深的比值为0.5时，浮鱼礁偏移量和正负偏转角度约等于0，即浮鱼礁保持静止。

图6 正负方向最大转角随水深变化

3.3 锚绳最大受力随波高变化

在水深8 m，波高分别为1.5、2、2.5、3 m的工况下，锚绳的最大拉力变化如图7所示。

图7 锚绳最大拉力随波高变化

锚绳最大拉力随着波高的增加而增大，波高每增加0.5 m，锚绳最大受力约增加40 N，近似呈线性变化。计算发现锚绳最大拉力位置出现在水底锚碇点处。因此，在实际安装时要充分考虑到当极端天气出现时，锚碇点的极限抗拨能力，保证整个浮鱼礁系统的安全性。

3.4 锚绳最大受力随水深变化

图8中的两条线分别代表当波高3 m时锚绳的最大拉力和波高0 m时的锚绳拉力。从图中可以看出，锚绳的最大拉力随着水深的增加而减小，当水深从8 m到10 m时，锚绳最大拉力呈对数函数减小，从10 m开始，随着水深增加，锚绳最大拉力变化缓慢，当水深11 m时，锚绳的最大拉力几乎和静水时的拉力相等，并在其附近小幅度震荡，震荡的原因与锚绳的弹性应变系数有关。当水深超过11 m时，锚绳的最大拉力随着水深的增加几乎没有变化。同样，锚绳最大拉力位置出现在水底锚碇点处。综上所述，水深的变化对锚绳最大拉力的影响十分显著，随着水深的增加，浮鱼礁浮体附近的水质点速度迅速减小，当水深超过11 m时，水质点运动速度接近于0，此时浮鱼礁浮体受波浪力几乎为0 N。实际在海洋牧场布置浮鱼礁时，必须依据当地海域的潮位变化，按照低潮位时计算锚绳的最大受力，评估浮鱼礁的安全性能。

图8 锚绳最大拉力随水深变化

4 结论

通过数值模拟方法研究了框架式浮鱼礁在波浪条件下的水动力特性。当水深一定时，波高每增加0.5 m，浮体最大水平偏移约增加0.05 m，浮体正负向最大偏转转角增加1.2°，负向最大偏转转角增加1.4 °，锚绳最大受力增加40 N，锚绳最大张力发生在水底锚碇点处。波高一定，当相对入水深度小于2/5时，浮体最大水平偏移、最大偏转角度和锚绳最大拉力随水深增加而急剧减小；当超过2/5时，则随水深增加变化缓慢；当达到1/2时，前两项几乎没有变化，锚绳最大拉力和静水时锚绳拉力几乎相等。在实际海洋牧场建设中，投放浮鱼礁应考虑目标海域潮差和潮位变化导致相对入水深度变化带来的影响。当相对入水深度小于2/5时，其变化对锚绳的拉力和浮体的运动都有十分剧烈的影响。水深一定时，波高的变化也会对锚绳受力和浮体运动产生影响，因此，在设计浮鱼礁时，应将低潮位时的水深及设计波高作为设计动力，从而选取合适的锚绳和浮体的投放位置，保证浮鱼礁投放的有效性和安全性。

□

参考文献

[1] 周艳波,蔡文贵,陈海刚,等.人工鱼礁生态诱集技术的机理及研究进展[J].海洋渔业,2010,32(2):225-230.

[2] SHERMAN R L,GILLIAM D S,SPIELER R E. Artificial reef design:void space,complexity,and attractants [J]. ICES Journal of Marine Science,2002,59(S):196-200.

[3] 林承刚,汝少国,杨红生,等.刺参对人工礁体设计关键指标的选择性[J].海洋科学,2012,36(3):13-21.

[4] PEDRO G,MARCOS F,LUCIANO D S,et al. Impact of artificial patchy reef design on the ichthyofauna community of seasonally influenced shores at Southeastern Brazil[J]. Aquatic Ecology,2015,49(3):343-355．

[5] 陈勇,于长清,张国胜,等.人工鱼礁的环境功能与集鱼效果[J].大连水产学院学报,2002(1):64-69.

[6] 赵海涛,张亦飞,郝春玲,等.人工鱼礁的投放区选址和礁体设计[J].海洋学研究,2006(4):69-76.

[7] 刘惠飞.日本人工鱼礁研究开发的最新动向[J].渔业现代化,2002,29(1):25-27.

[8] 夏章英,卢伙胜,冯波,等.人工鱼礁工程学[M].北京:海洋出版社,2011:80-81.

[9] 余求妹,马家志,安玉,等.浮绳式网箱人工浮鱼礁的设计优势及问题的探讨[J].安徽农业科学,2013,41(19):8194-8195,8217.

[10]张丽珍,王江涛,胡庆松,等.近海中上层柔性浮鱼礁设计与应用[J].上海海洋大学学报,2016,25(4):613-619.

[11]余建星,韩彤,李林奇,等.海洋资料浮标水动力特性研究现状分析[J].海洋湖沼通报,2017(4):61-67.

[12]李文涛,张秀梅.关于人工鱼礁礁址选择的探讨[J].现代渔业信息,2003(5):3-6.

[13]张剑诚,金海,王吉桥.人工渔礁建设研究现状[J].水产科学,2004(11):27-30.

[14]王彩云. HDPE高密度聚乙烯管道的应用研究[J].企业技术开发,2012,31(14):159-160.

[15]赵云鹏.深水重力式网箱水动力特性数值模拟研究[D].大连:大连理工大学,2007.

[16]赵云鹏,李玉成,董国海,等.水流作用下重力式网箱网衣张力分布[J].渔业现代化,2008,35(6):58-63.

[17]桂福坤.深水重力式网箱水动力学特性研究[D].大连:大连理工大学,2006.

[18]陈小芳.鲆鲽类方形网箱水动力特性数值模拟[D].大连:大连理工大学,2012.

[19]陈天华,孟昂,桂福坤.波浪高度及方向对桩柱式围网养殖系统网片水力特性的影响[J].农业工程学报,2017,33(2):245-251.

[20]李玉成,桂福坤.平面无结节网衣水阻力系数的试验研究[J].海洋学报,2006,28(5):145-151.

[21]杨正东,朱建荣,王彪,等.长江河口潮位站潮汐特征分析[J].华东师范大学学报(自然科学版),2012(3):111-119.