基于模态法L形工装结构冲击动力学仿真分析

薛 杰，许红卫，杜大华，何志勇，李 锋

(液体火箭发动机技术重点实验室，陕西 西安 710100)

0 引言

在航空航天、化工、兵器、船舶等工程领域，人们已经越来越多地认识到冲击环境对结构带来的影响，轻者减少产品结构寿命、降低产品性能指标，重者直接导致产品功能丧失及结构破坏。因此，为确保产品结构安全、可靠运行，往往需要通过特定的冲击试验来考核冲击环境下结构的适应性或从中寻找结构的薄弱环节，并进行结构改进。通常情况下，被试结构通过工装转接后固定于振动台或冲击台上进行试验，控制点一般位于在台面，尤其是利用冲击台进行试验时，控制传感器几乎均安装于冲击台面上。工装固有的动力学特性可能使得台面与被试结构安装面的冲击响应存在较大差别，使得产品存在过或欠试验考核的风险。因此，研究转接工装的动力学特性以及冲击环境下的动力学响应就显得格外重要[1-3]。

L形工装常用来转接被试结构以实现不同方向的冲击试验。本文基于有限元理论，结合模态试验、冲击响应谱试验对L形工装进行模态分析及冲击动力学仿真分析。分析结果一方面说明模态法在冲击动力学仿真分析中具有一定的可行性；另一方面对冲击试验中控制点的布置具有一定的指导意义。

1 有限元模型及计算方法

1.1 有限元模型

基于MSC/Patran前处理软件，建立的L形工装有限元模型见图1。计算模型中，忽略三角支板、方形立板及底板相互间的导角，同时不考虑方形立板上的小孔特征。为保证模型具有较高的准确性和精度，模型均采用10节点4面体二阶单元模拟。L形工装与振动台台面的两种连接处理方法如下：

方法1：建立用于模拟振动台台面的6个虚拟自由度，通过采用不同的刚性约束单元连接14个螺栓孔与虚拟自由度的方式来模拟14个螺栓孔与振动台的固定。

方法2：建立用于模拟振动台台面的6个虚拟自由度，通过采用刚性约束单元连接底板下端面的方式来模拟L形工装与振动台的固定。

最后，模态分析与冲击动力学分析的计算边界条件或载荷条件均通过适当的方式施加于虚拟自由度上。

L形工装结构材料为ZL101，材料性能参数如表1所示。

表1 L形工装材料参数

图1 L形工装及其有限元模型Fig.1 L-shaped fixture and its finite element model

1.2 计算方法

1.2.1 模态分析基本理论

无阻尼结构系统的自由振动微分方程：

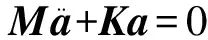
(1)

通过简单推导可以得到表示特征值问题的代数方程组，即：

(2)

式中：M为结构系统的质量矩阵；K为结构系统的刚度矩阵；Φi代表结构系统的某阶模态向量(模态振型)；a为位移向量；ωi代表结构系统的某阶模态角频率。

目前对式(2)进行特征值求解的数值方法有很多[4-5]，本文采用近些年应用较多且效果较好的Lanczos方法[6-7]完成结构的模态计算，该方法的优点是不会丢失特征根。

1.2.2 模态法瞬态分析基本理论

对结构无阻尼运动微分方程：

(3)

首先利用模态向量矩阵Φ进行空间转换，即 代入方程(3)得到：

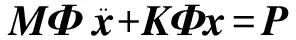
(4)

式中：x为模态坐标向量；P为外载荷向量。为了解耦，对方程(4)前乘ΦT，并利用模态振型Φ的正交特性[8]得到：

式中：mi为第i阶模态质量；ki为第i阶模态刚度；pi为第i阶模态力；xi为第i阶模态坐标。再利用第i阶模态角频率ωi，并引入第i阶模态阻尼比ξi得到第i阶模态运动方程：

(5)

利用杜哈梅积分[6，9]对每阶模态运动方程的模态坐标进行求解，最后经过模态矩阵叠加得到物理坐标的解a。本文在冲击动力学计算中取结构的前10阶模态进行计算。

2 L形工装模态试验

为了检验并修正有限元动力学分析模型，初步确定模型中参与计算的各阶模态阻尼比，开展L形工装固定于振动台状态的模态试验。

实际结构试验状态、试验模型及其分析坐标系如图2所示。其中，试验模型由16个点组成，每个点采用三向传感器测试。为保证模态试验结果的完整性，根据结构的特点，激励点取10号、11号、12号及13号点，激励方向包括X方向及Y方向，脉冲激励由试验力锤敲击产生。分析频率范围：0～2 048 Hz，频率分辨率为1 Hz。

通过试验数据的处理分析[10]，得到L形工装结构前6阶模态试验结果，如表2所示，各阶模态振型如图3和图4所示。

图2 L形工装及其模态试验模型Fig.2 L-shaped fixture and its modal test model

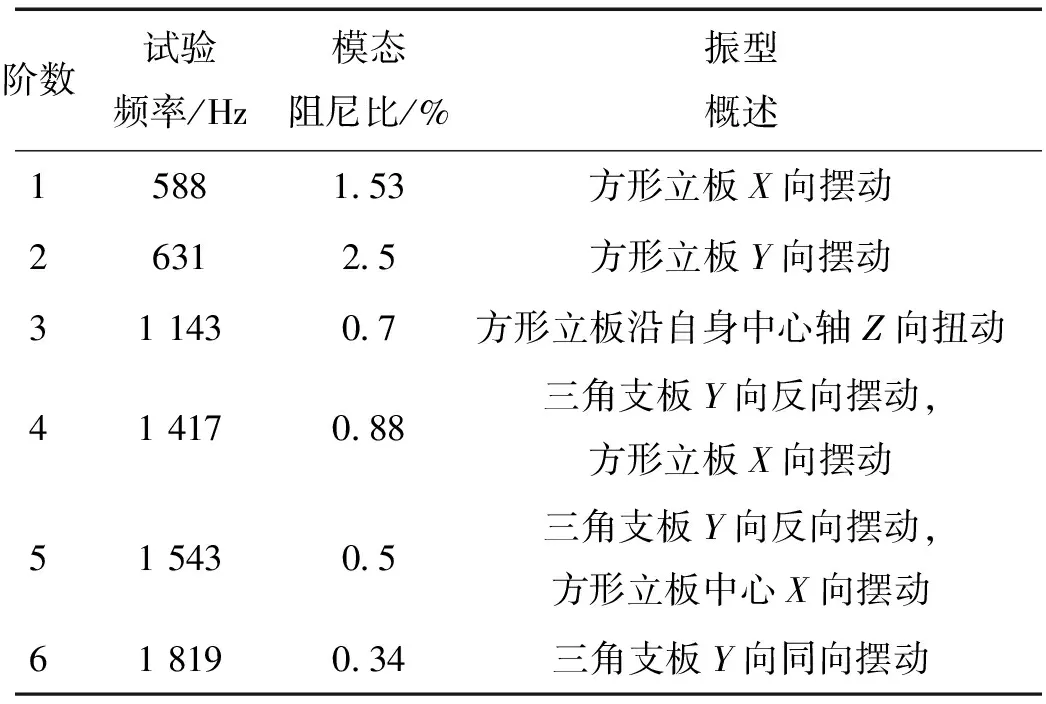
阶数试验频率/Hz模态阻尼比/%振型概述15881 53方形立板X向摆动26312 5方形立板Y向摆动311430 7方形立板沿自身中心轴Z向扭动414170 88三角支板Y向反向摆动，方形立板X向摆动515430 5三角支板Y向反向摆动，方形立板中心X向摆动618190 34三角支板Y向同向摆动

图3 L 形工装前3阶模态振型Fig.3 The first three modal shapes of L-shaped fixture

图4 L 形工装第4阶至第6阶模态振型Fig.4 The fourth to sixth modal shapes of L-shaped fixture

3 模态计算结果

基于第1节的计算模型及计算方法，得到L形工装固定于振动台状态下，两种不同连接处理方法的前6阶模态计算结果，如表3所示。其中，虚拟自由度全部约束用于模拟振动台台面固定。方法1模态计算振型见图5和图6所示，方法2模态计算振型如图7和图8所示。

表3 模态计算结果与试验结果的比较

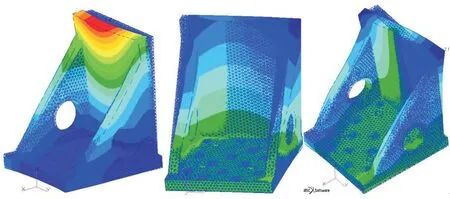
图5 方法1前3阶模态振型Fig.5 The first three modal shapes based on first method

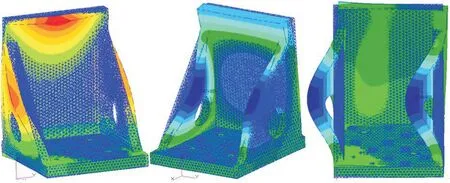
图6 方法1第4至第6阶模态振型Fig.6 The fourth， fifth and sixth modal shapes based on first method

图7 方法2前3阶模态振型Fig.7 The first three modal shapes based on second method

图8 方法2第4至第6阶模态振型Fig.8 The fourth， fifth and sixth modal shapes based on second method

从模态频率、模态振型的计算结果与试验结果的对比来看，方法1更能准确反映实际状态；方法2的频率计算结果与试验相差较大。其中第2阶相差达到70.8%，而第4阶模态振型与试验结果也存在明显差异，因此，后续响应计算采用方法1模拟L形工装与振动台台面的连接。

4 L形工装冲击仿真模拟及其试验

上述计算模型结合模态试验得到的阻尼参数，采用模态叠加法对L形工装进行X向冲击响应谱试验的动力学仿真。冲击响应谱试验条件及其转换后的加速度时域数据如图9所示，转换参数主要包括品质因子Q=10及持续时间t=0.25 s。由于冲击激励经过约0.064 s，量级几乎衰减为0，因此，冲击仿真分析时间定为0.064 s。分析中不考虑材料非线性。

计算激励：加速度时域数据加载于X向虚拟自由度。

计算边界：除X向外，约束其他5个虚拟自由度。

图9 冲击响应谱试验条件Fig.9 Test conditions of SRS

经过有限元计算及冲击响应谱试验，分别得到L形工装立板中间A2点X向加速度响应谱的计算曲线及试验曲线，如图10所示。冲击响应谱试验中A2点的实际响应量级在3个频段内比计算结果明显偏小，分析认为这是由于L形工装与振动台台面间螺栓连接的刚度偏小，导致工装底面与振动台台面接触边界的边界非线性增强所致。因此，为弥补边界非线性给机械能带来的损失，在采用模态叠加法进行瞬态动力学分析中应该适当提高相应的模态阻尼比，修正前后模态阻尼比的具体数值如表4所示。

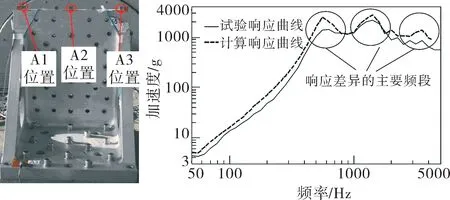
图10 L形工装A2点加速度冲击响应谱的计算值与试验值Fig.10 Calculation results and test results of accelerated SRS at A2 in L-shaped fixture

表4 修正前后的模态阻尼比

采用修正后的模态阻尼比，得到L形工装A2点X向加速度冲击响应谱的计算曲线与试验曲线的对比、冲击时域响应的计算曲线与试验曲线的对比，分别如图11和图12所示。对比结果显示计算曲线与试验曲线基本一致，因此，可以认为上述模态阻尼比的修正有效。另外，给出L形工装立板两端A3，A1两点冲击响应谱的试验曲线及计算曲线，分别如图13和图14所示。

上述结果表示，L形工装冲击动力学模型修正后的仿真分析基本可以正确预示结构的冲击动力学响应，特别是2 000 Hz以下具有较高的预测精度。同时，通过计算，获取结构上4个关键位置S2，S4，S5及S7(图1)Z方向的冲击应变数据，并计算其冲击响应谱[11]，如图14所示。结果表示：上述冲击过程中，L形工装结构关键位置产生较大的动应变主要来自2 000 Hz以下的冲击响应。

图11 阻尼修正后L形工装A2点加速度冲击响应谱的计算值与试验值Fig.11 Calculation results and test results of accelerated SRS at A2 in L-shaped fixture after damping adjustment

图12 阻尼修正后L形工装A2点加速度时域响应的计算与试验对比Fig.12 Comparison between calculation results and test results of accelerated time-domain response at A2 in L-shaped fixture after damping adjustment

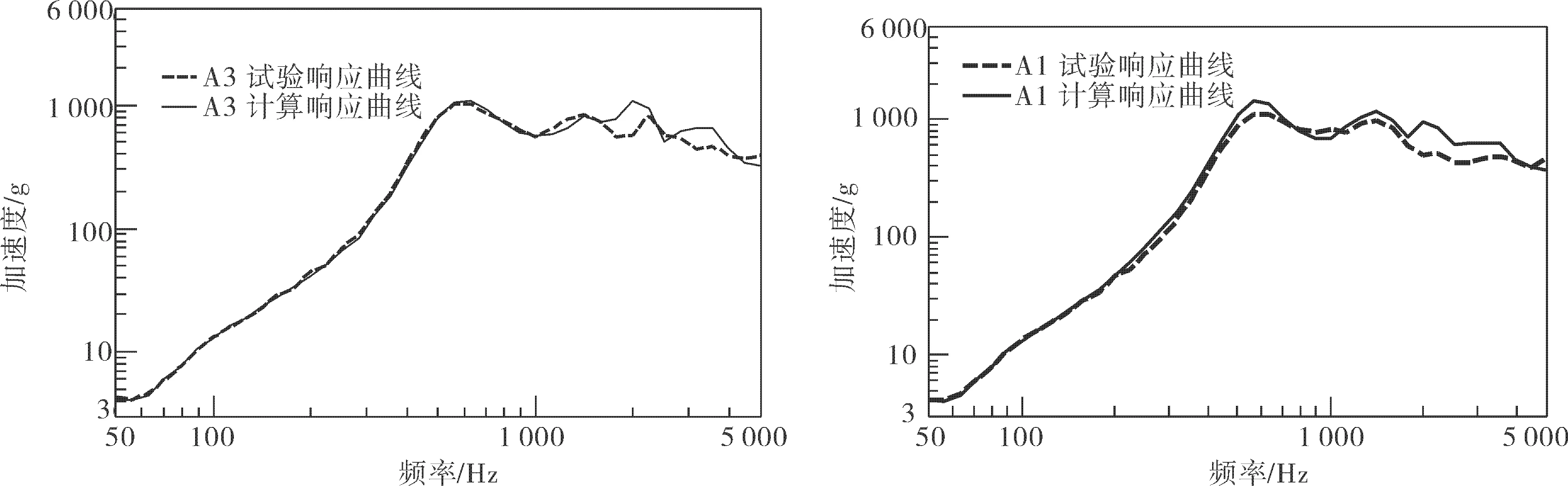
图13 阻尼修正后L形工装A3、A1点加速度冲击响应谱的计算与试验对比Fig.13 Comparison between calculation results and test results of accelerated SRS at A3 and A1 after damping adjustment

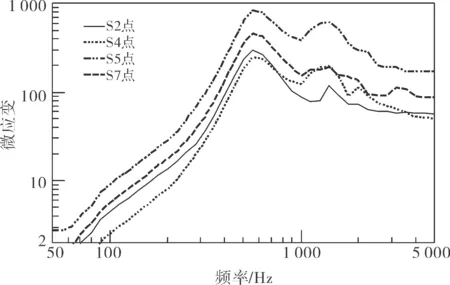
图14 应变冲击响应谱计算结果Fig.14 calculation results of strain SRS

5 L形工装不同位置的冲击响应

基于上述修正后的L形工装有限元动力学模型，分析被试结构固定在L形工装4个不同位置上冲击响应谱的特征及差异。其中，认为被试结构质量为0.5 kg，采用集中质量单元模拟。被试结构与工装的连接采用RBE2刚性约束单元模拟，得到固定于1#位置的仿真模型，如图15所示。

图15 连接被试结构的L形工装仿真模型Fig.15 Simulation model of L-shaped fixture connecting the structure under test

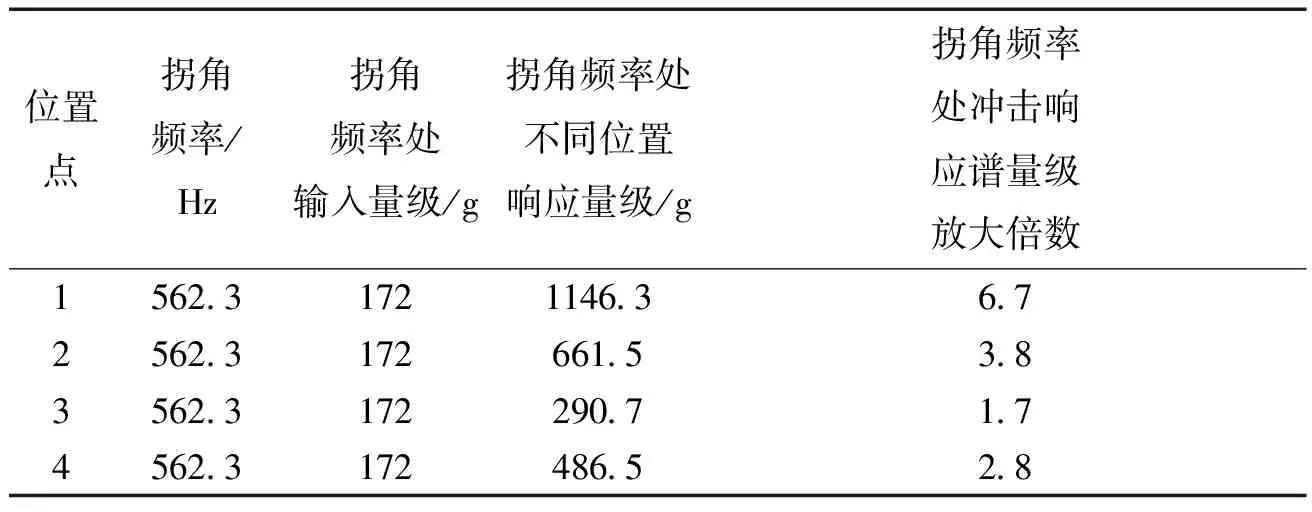
通过计算，得到固定于L形工装不同位置被试结构X向的冲击响应谱与输入条件谱，如图16所示，表5给出被试结构在不同安装位置下冲击响应谱的拐角频率及其量级。

图16 L形工装不同位置处X向加速度冲击响应谱计算结果Fig.16 Calculation results of accelerated SRS in X direction at different position of L-shaped fixture

位置点拐角频率/Hz拐角频率处输入量级/g拐角频率处不同位置响应量级/g拐角频率处冲击响应谱量级放大倍数1562 31721146 36 72562 3172661 53 83562 3172290 71 74562 3172486 52 8

从图16及表5的计算结果中可以得到：

1)在4个不同的安装位置，被试结构冲击响应谱的拐角频率均为562.3Hz，该频率值与L形工装的一阶频率计算值密切相关。

2)被试结构拐角频率处不同位置响应量级比输入量级均有不同程度的放大，其中1#位置点放大倍数最大为6.7；3#位置点放大倍数最小为1.7。

3)被试结构4个不同安装位置的冲击响应谱形与L形工装输入谱形均存在较大差异，具体表现为不同安装位置的冲击响应谱量级在L形工装一阶频率处放大、高频段减小。

6 结论

基于模态法对冲击试验中常用的L形工装进行了冲击动力学仿真，可以得到以下结论：

1)在工装与试验台的连接处理中，通过建立用于模拟试验台面的虚拟自由度，并采用不同的刚性约束单元连接螺栓孔与虚拟自由度的方式可以获得更为精确的计算模型。

2)为弥补边界非线性给机械能带来的损失，在采用模态叠加法对L形工装进行瞬态冲击动力学分析中应该适当提高相应的模态阻尼比。

3)为避免过试验或欠试验，保证被试结构所承受的冲击响应谱与试验条件一致，控制点应当尽可能选择被试结构安装面位置。

参考文献：

[1] 田海英， 聂品， 董斌， 等. 一种航空遥感器动力学环境试验工装的设计与分析[J]. 长春理工大学学报(自然科学版)，2012，35(4): 18-20 .

[2] 王东升， 任万发， 刘青林， 等. 振动试验夹具共振频率设计要求研究[J]. 航天器环境工程， 2014，31(1): 37-41 .

[3] 宫晓春， 李彩霞， 陈严华， 等. 应用圆盘工装谐振实现高量级随机振动[J]. 航天器环境工程， 2015，32(3): 273-277 .

[4] 王勖成. 有限单元法[M]. 北京: 清华大学出版社， 2003.

[5] 徐稼轩， 郑铁生. 结构动力分析的数值方法[M]. 西安: 西安交通大学出版社， 1993.

[6] MSC Software Corporation. Dynamic analysis user’s guide(MSC Nastran 2013)[M]. United States：MSC Software Corporation， 2013.

[7] 杨剑， 张璞， 陈火红. MD Nastran有限元实例教程[M]. 北京: 机械工业出版社， 2008.

[8] 李德葆， 陆秋海. 实验模态分析及其应用[M]. 北京: 科学出版社， 2001.

[9] 方同， 薛璞. 振动理论及其应用[M]. 西安: 西北工业大学出版社， 2010.

[10] LMS Test Lab. Estimation of modal parameters (Rev 12A) [G]. [S.l.]: LMS Test Lab， 2012.

[11] 何志勇， 宋少伟， 邓长华， 等. 瞬态时域数据合成冲击响应谱算法研究[J]. 火箭推进， 2013，39(5): 55-59 .

HE Zhiyong， SONG Shaowei， DENG Changhua， et al. Research on transient time-domain data synthesis of shock response spectrum [J]. Journal of rocket propulsion， 2013， 39(5): 55-59.