一种基于SVM的低空飞行冲突探测算法

韩冬， 张学军,*， 聂尊礼， 管祥民

(1. 北京航空航天大学 电子信息工程学院, 北京 100083； 2. 中国民航管理干部学院, 北京 100102)

复杂低空受多样多变地形、障碍物和极端恶劣气象等复杂环境要素的约束，有限空域内多航空器的密集飞行呈现出高度复杂的时空相互制约性[1]，基于航路航线冲突探测的一些假设条件在低空中并不适用。此外，由于低空冲突探测以短期预测为主，冲突探测必须在极短的时间内完成，这样才能保证在有限的时间、空间裕度内实施有效的躲避策略。综合考虑适用性与计算效率，是低空飞行冲突探测的难点所在。

国内外对于冲突探测的研究主要分为确定型(也称几何型)和概率型(也称解析型)2类。确定型冲突探测[2-4]一般采用计算几何的方法，判断2架航空器在相遇几何内是否存在潜在飞行冲突。但是实际情况下存在风、导航定位、飞行员操作等不确定性因素引起的误差，将直接影响到冲突探测的准确度。概率型冲突探测[5-7]则通过计算航空器之间的冲突概率，以解析的方法确定是否存在潜在飞行冲突，但是阈值的选取十分关键：如果阈值选取过大，可能造成漏警；如果阈值选取过小，则可能造成大量的误警[8]。

传统的空中交通警戒与防撞系统(Traffic Alert and Collision Avoidance System,TCAS)是当前广泛应用的机载避撞系统[9]，主要为飞行员提供空-空碰撞告警。TCASⅠ只提供碰撞告警服务，TCASⅡ除了告警外，还提供冲突解脱建议，但只是简单的爬升和下降机动，此外TCASⅡ在1 000 m以下低空存在较高的虚警率，在通用航空上应用并不广泛[10]。广播式自动相关监视(Automatic Dependent Surveillance-Broadcast，ADS-B)设备结构简单，成本较低，信息更新速率快，监视精度较高，已经广泛用于高空航线飞机和低空通航飞机上[11]。

Lin[12]根据TCAS检测逻辑，设计了一种基于ADS-B和目视飞行规则的针对低空通航小飞机的空域冲突探测和解脱方法。焦玉亮等[13]采用支持向量机(Support Vector Machine,SVM)，提出一种针对高空航路的水平二维冲突探测方法。

考虑到通用航空一般在特定空域内飞行，在相对固定的飞行环境中，可以获取丰富的历史飞行数据，通过提前分析这些先验数据，挖掘数据关联特征，提取飞行冲突探测的判定依据，是一种解决低空复杂飞行冲突探测问题的新思路。航空器可以在起飞前加载经过训练的分类器，减少飞行中在线解算的时间，有效解决传统冲突探测算法难以兼顾适用性与解算效率的缺陷。

1 基于SVM的冲突探测

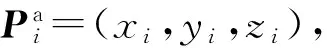
检测系统的结构如图1所示。

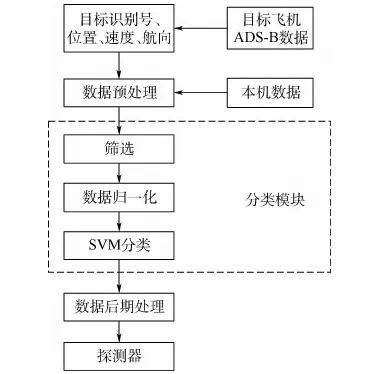
图1 检测系统结构

1.1 数据预处理

数据预处理主要计算目标飞机相对于本机的位置、速度和航向等信息。

为了简化模型，保护区设置为半径528 ft(1 ft=0.304 8 m)的球形，如图2所示。

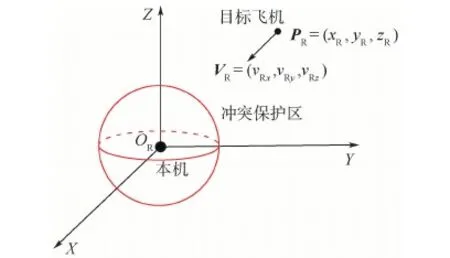
图2 保护区模型

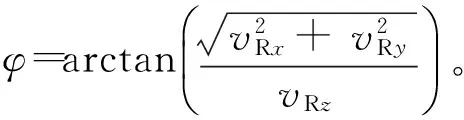
相对水平航向是以相对坐标系的X轴正方向为基准的。

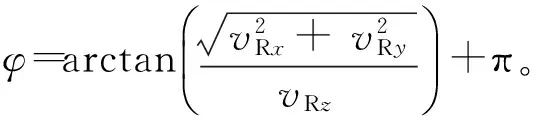
2) 如果目标飞机的相对速度vRx<0,vRy>0或者vRx<0,vRy<0,水平相对航向为

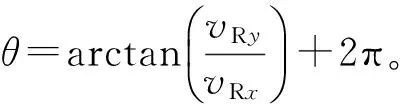
垂直航向是以相对坐标轴中Z轴正方向为基准。

1.2 SVM模块

在将经过预处理的数据输入SVM模块后，笔者首先将数据进行过滤处理，将一些一定不会发生冲突的目标提前进行分类处理，如表1所示。

经过训练的SVM分类器对经过过滤和归一化的输入数据进行分类。对于所有的分类目标，如果在t时刻目标为存在潜在冲突可能，则在假设对于第i架飞机在t时刻的预测值为Pt(Ti)=1，如果目标在t时刻经过SVM分类检测不存在冲突可能，则Pt(Ti)=-1。

数据后期处理主要采用移动平均加权，考虑到对飞机的冲突检测是一个连续的过程，在某个时间点对冲突进行探测，需要考虑前一段时间的预测结果。移动加权平均的滑动窗口为m，滑动加权系数w={wt-m+1,…,wt-1,wt}，则对于第i架飞机在t时刻经过移动加权平均后的预测值为

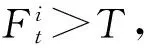
表1 无冲突判定准则

2 支持向量机

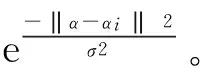
通过选取适当的核函数及相应的参数，以及惩罚因子C,可以建立一个适当的分类模型对数据进行分类。所以，参数的选取是建立SVM模型的重要步骤。本文选取径向基函数作为其核函数，涉及到的参数有C和σ。

C主要影响建立SVM模型的复杂度。较高的C使得模型的复杂度高，但模型的推广能力差，C越低，建立的模型越简单，模型的推广能力越高。较高的C虽然使得模型训练准确度高，但是对于预测样本的分类正确率低。

σ控制了径向的作用范围，σ越高，对于特征数据的映射能力越弱，σ越低，映射能力越强，但是可能会造成过拟合的情况。

传统的参数选取的方法包括网格搜索(Grid-Search)法和经验选择法，经验选择法虽然简单，但是存在很大的主观性。网格搜索法在一定的搜索空间中以一定的步进逐步搜索，但是存在计算量大，搜索精度不足等问题。

近年来，国内外许多研究学者采用进化算法对SVM的参数进行选取。常用的有遗传(GA)算法和粒子群(PSO)算法。GA算法借鉴生物界中生物进化繁衍的规律，通过对个体的选择、交叉、变异等操作来寻找解空间的潜在最优解。但是GA算法具有较大的随机性，且算法本身的参数设置过多，容易产生早熟收敛等问题。PSO算法模拟鸟群捕食行为，通过考虑粒子的个体最优值和全体最优值来引导粒子的搜索策略。但是PSO算法同样存在容易陷入局部最优的情况，切对于粒子的初始值比较敏感。所以本文结合GA和PSO算法各自的优点，提出一种GA-PSO混合算法，来解决SVM的参数寻优问题，训练流程如图3所示。

2.1 GA-PSO混合算法

PSO算法粒子种群由n个粒子组成X=(X1,X2,…,Xn)，每一个粒子位置Xi=(xi1,xi2,…,xiD)，D为解空间的维数；每一个粒子的速度为Vi=(Vi1,Vi2,…,ViD) ，以K类交叉验证(cross-validation)[15]正确率作为粒子的适应度函数P。

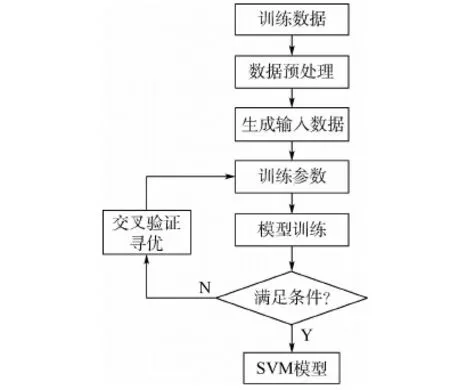
图3 GA-PSO混合算法训练流程

所谓K类交叉验证，就是将训练集平均分为K份，每次取1份作为测试集，剩余的K-1份作为训练集，然后采用当前的参数取值，也就是粒子位置Xi=(xi1,xi2,…,xiD)作为训练参数时进行模型的建立和对测试集的分类，最后将K个模型的分类正确率平均。个体极值为Pi=(Pi1,Pi2,…,PiD)，全局极值为Pg=(Pg1,Pg2,…,PgD)，粒子的更新公式为

式中：k为种群的当前迭代次数；c1、c2为加速度常数；r1、r2为(0,1)之内的随机数。

粒子的位置变化幅度是由粒子的飞行速度的大小决定的，粒子飞行速度大，能够在短时间内飞到搜索空间中最优解的区域，其全局搜索能力较强，粒子飞行速度较低时，粒子的位置变化幅度较小，有利于增加搜索的精度，局部搜索能力强，全局搜索能力弱。但是，如果粒子的飞行速度一直保持一个较高的值，可能会导致粒子越过最优解区域，飞行速度一直较低的时候，虽然搜索的精度会增加，但是可能导致粒子陷入局部最优解。所以对速度更新公式增加了一个加权系数：

式中：g为当前迭代次数；G为最大迭代次数。以此，粒子在迭代初期能够保持较高的更新速度，以获得较强的全局搜索能力，在迭代后期具有较低的更新速度，具有较强的局部搜索能力，w变化曲线如图4所示。

在算法迭代初期，为了加大粒子的不确定度，增强算法的全局搜索能力参考遗传算法的机理，对粒子进行变异，具体流程如图5所示。

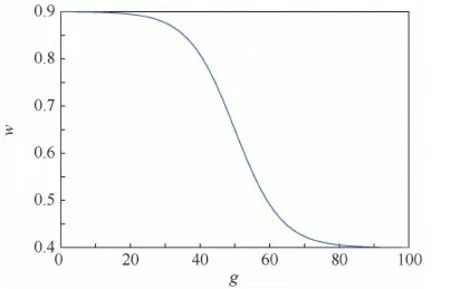
图4 w变化曲线

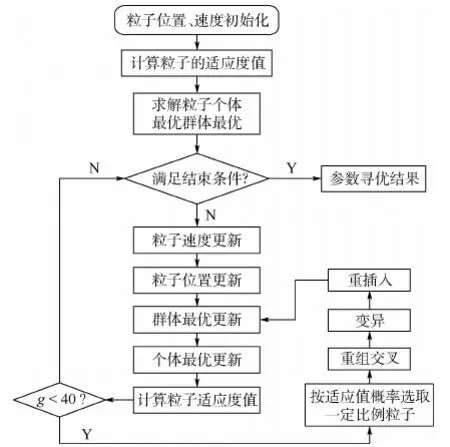
图5 粒子变异流程

步骤1设定种群规模和迭代次数,搜索空间大小和速度大小等参数。根据限制随机初始化粒子的位置X=(X1,X2,…,Xn)和速度V=(V1,V2,…,Vn)。

步骤2根据每个粒子的位置Xi=(xi1,xi2)对模型进行训练，将交叉验证正确率作为该粒子的适应度。

步骤3根据每个粒子的适应度和其历史位置上的适应度相比较，将适应度较高的作为新的个体极值Pi=(Pi1,Pi2,…,PiD)。

步骤4根据每个粒子的适应度和所有粒子经过的最优适应度相比较，将适应度较高的作为新的全局极值Pg=(Pg1,Pg2,…,PgD)。

步骤5根据粒子的速度和位置更新公式对粒子进行更新。

步骤6迭代次数是否满足条件g<40，若满足进行步骤7，是否满足最大迭代次数，如果满足，输出结果，若不满足，返回步骤3。

步骤7计算粒子的适应度值，根据粒子适应度的大小按一定比例选从种群Z取出种群Z2。

步骤8对Z2进行重组交叉。

步骤9对Z2进行变异。

步骤10计算Z2的适应度，根据适应度重插入种群Z中，保留适应度高的，排除适应度低的。

步骤11返回步骤3。

2.2 算法比较

实验的相关参数设置如表2所示。

采用5-折交叉验证，分别生成了3组训练数据，比较GA、PSO和GA-PSO 3种算法的寻优性能。训练数据为经过过滤和归一化的目标飞机状态信息，包含目标飞机的相对位置、相对速度和相对航向角等信息，如表3所示。

记录训练过程中的每一代的交叉验证正确率，针对每组数据，采用3种算法分别进行50次寻优，记录训练过程中每一代的平均正确率。图6为训练数据样本为200个的时候，训练过程中，交叉验证过程适应度的变化。

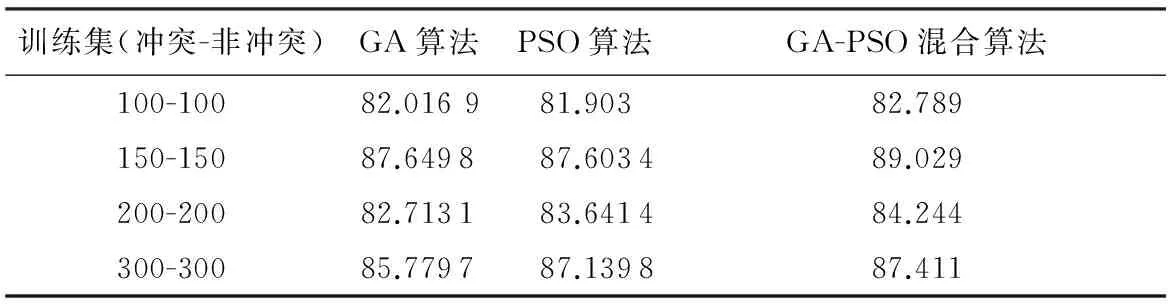
将50次的训练结果作为参数去分别训练SVM模型，并对测试数据进行预测分类，测试数据为目标飞机相对状态信息，其中一半为冲突状态，另一半为非冲突状态。

平均正确率统计如表4所示。

可以看出，GA-PSO混合算法能够克服原GA和PSO算法过早收敛的不足。由于寻优前期较大的随机性和随着训练代数而变化的粒子速度。由于GA-PSO混合算法具有较好的全局寻优能力，在局部寻优时也有较好的准确性，其能够搜索到更优的解。

表2 3种算法参数

注：N/A表示不适用。

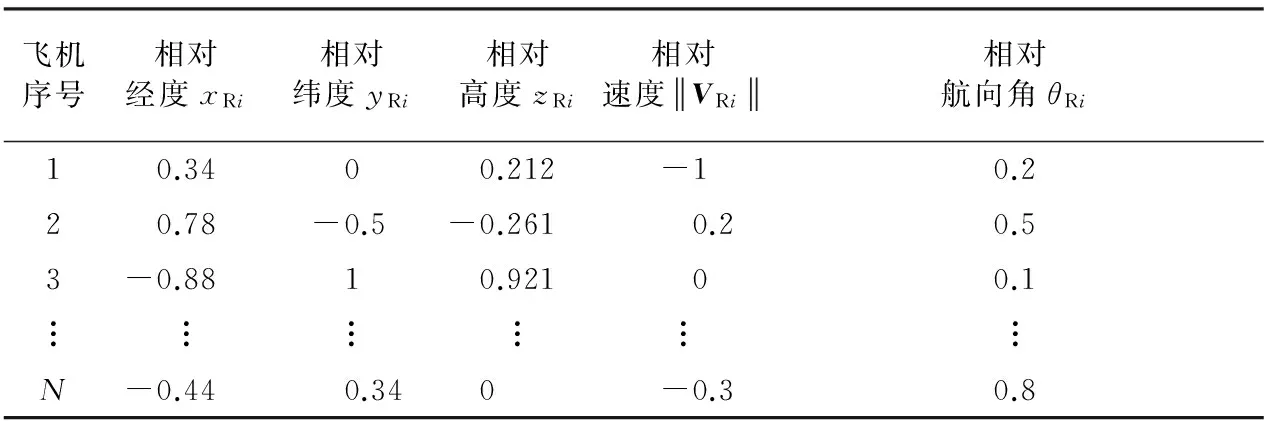
表3 归一化飞行状态

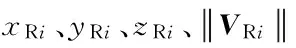
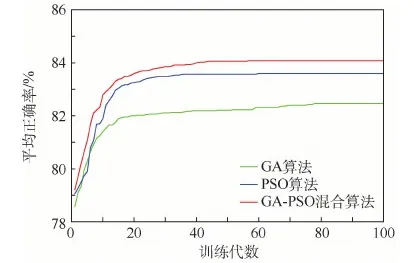
图6 交叉验证平均正确率

3 仿真分析

以经典的CESSNA 172单引擎飞机作为目标参考(其主要参数见表5)，生成了4 000个作为训练数据，其中包含2 000个冲突飞机的特征数据，2 000个不冲突飞机的特征数据，相对位置坐标位于本机水平范围0.9～3.0 nmi(1 nmi=1.852 km)。选取RBF径向基核函数，采用GA-PSO混合算法寻得训练参数。

采用蒙特卡罗方法对该方法的性能进行分析，生成测试数据一共20组，每组一共包含500个航迹信息，250个冲突航迹和250个不冲突的航迹，航迹的初始相对位置位于本机监视范围1.3～3.0 nm之间，针对每个航迹，进行持续10 s的检测时间，监视范围为水平1～3 nm，如果目标飞机位置处于在水平监视范围以外时停止检测，垂直检测范围为1 000 m以下，测试统计结果如表6所示。

表5 CESSNA 172的尺寸和性能

注：最大承载人数为4。

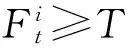
表6 用于检测的统计数据

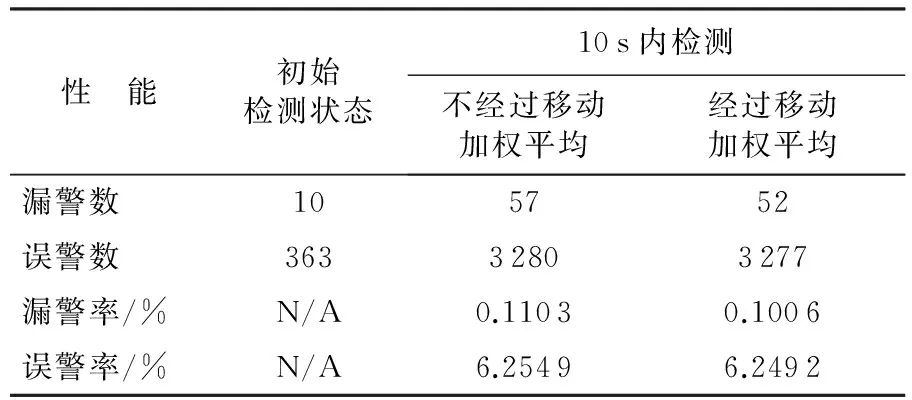
表7 检测系统性能的统计数据

4 结 论

1) 本文提出的基于SVM的冲突探测算法，将冲突探测问题转化为一个规划求解的问题。首先对ADS-B报文数据进行筛选和归一化处理，其次通过GA-PSO混合算法完成SVM的参数选优，并通过先验信息对SVM进行训练，最后通过移动加权平均，优化SVM分类判定结果，实现了基于SVM的飞行冲突探测。

2) 通过对比参数优化及探测能力实验结果，GA-PSO混合算法在参数优化上性能优良，确保训练后的SVM在冲突探测时保持了较高的正确率和解算速度，本文算法适用于解决低空复杂飞行冲突探测问题。

参考文献(References)

[1] GARIEL M,HANSMAN R,FRAZZOLI E.Impact of GPS and ADS-B reported accuracy on conflict detection performance in dense traffic:AIAA-2011-6893[R].Reston：AIAA,2011.

[2] FULTON N L.Airspace design:Towards a rigorous specification of complexity based on computational geometry[J].Aeronautical Journal,1999,103(1020):75-84.

[3] CHIANG,YI J,KLOSOWSKI J,et al.Geometric algorithms for conflict detection and resolution in air traffic management[C]∥36th IEEE Conference on Decision and Control.Piscataway,NJ:IEEE Press,1997,2(2):1835-1840.

[4] MCDONALD J,VIVONA R.Strategic airborne conflict detection of air traffic and area hazards：NAS2-98005[R].Washington,D.C.:NASA,2000.

[5] PRANDINI M,HU J,SASTRY S.A probabilistic approach to aircraft conflict detection[J].IEEE Transactions on Intelligent Transportation Systems,2000,1(4):199-220.

[6] JARDIN M R.Grid-based strategic air traffic conflict detection:AIAA-2005-5826[R].Reston：AIAA,2005.

[7] HU J.Aircraft conflict detection in presence of spatially correlated wind perturbations:AIAA-2003-5339[R].Reston:AIAA,2003.

[8] 李彬,吴珍珍.基于航迹预测的飞行冲突预测[J].微处理机,2011(2):73-80.

LI B,WU Z Z.Flight conflict detection based on flight path prediction[J].Microprocessors,2011(2):73-80(in Chinese).

[9] 韩艳茹,敬忠良,龚嘉琦.空中交通预警与防撞系统(TCAS)风险及对策研究[J].计算机测量与控制,2012,20(3):737-740.

HAN Y R,JING Z L,GONG J Q.Research of traffic alert and collision avoidance system(TCAS) risk and countermeasure[J].Computer Measurement & Control,2012,20(3):737-740(in Chinese).

[10] WILLIAMSON T,SPENCER N A.Development and operation of the traffic alert and collision avoidance system(TCAS)[J].Proceedings of the IEEE,1989,77(11):1735-1744.

[11] 林熙.密集飞行条件下的间隔自主保持方法研究[D].北京：北京航空航天大学,2011:11-13.

LIN X.Research on self-separation assurance methods in condition of intensive flight[D].Beijing:Beihang University,2011:11-13(in Chinese).

[12] LIN C E.Collision avoidance solution for low-altitude flights[J].Proceedings of the Institution of Mechanical Engineers,Part G:Journal of Aerospace Engineering,2011,225(7):779-790.

[13] JIAO Y L,ZHANG X J,GUAN X M.An algorithm for airborne conflict detection based on support vector machine[J].Applied Mechanics and Materials,2012,229-231:1140-1145.

[14] CORTES C,VAPNIK V.Support-vector networks[J].Machine Learning,1995,20(3):273-276.

[15] KOHAVI R.A study of cross-validation and bootstrap for accuracy estimation and model selection[C]∥Proceedings of the 14th International Joint Conference on Artificial Intelligence.New York:ACM,1995:1137-1143.