一种跨声速定常流场求解加速方法

乔磊， 白俊强， 邱亚松,*， 华俊,2， 张扬

(1. 西北工业大学 航空学院, 西安 710072； 2. 中国航空工业集团有限公司 中国航空研究院, 北京 100012；3. 西安交通大学 航天航空学院， 西安 710049)

在飞行器和风力机械气动特性的评估和优化设计中，需要进行大量的定常流动模拟。在非定常数值模拟中，需要用定常流动的解作为初始解。因此，提高定常流场数值模拟的效率，可以使计算流体力学方法在气动外形设计应用中发挥更有力的作用。目前，常用的定常流动问题的控制方程是定常可压缩雷诺平均纳维-斯托克斯(Reynolds Averaged Navier-Stokes, RANS)方程，此方程是一个由对流项主导的非线性偏微分方程组，其求解分为显式和隐式2种方法。由于定常问题不需要考虑时间精度，隐式解法得以充分发挥其稳定性强、计算效率高的优点，因而得到了广泛的应用。

隐式解法的实质是非线性方程的牛顿迭代解法。牛顿迭代的优点是可以实现快速的平方收敛，但是要求初值足够接近方程的解才能避免发散。在实际应用中，一般情况下在迭代开始前是无法获得足够接近真实解的初值的。在外流流场模拟中，定常计算的初值通常为按自由来流条件设定的一个均匀场，直接应用牛顿解法往往会导致求解发散。因此，研究者们发展了多种类型的牛顿迭代全局化方法。

针对非线性问题的牛顿迭代全局化方法可以分为2种类型。第一类是不涉及非线性问题本身的方法。在这类方法中，比较常见的有网格序列法[1-2]和线性搜索法[3-4]。这类方法不是本文研究的重点，故不做深入介绍。因为这些方法独立于非线性问题本身，所以可以与本文所讨论的方法叠加使用，构造进一步提高求解效率的方法。另外一类方法是与非线性问题本身相关的。这类方法是通过修改所要求解的问题，保证迭代的收敛。针对定常流场模拟问题，这类方法的典型代表有边界松弛(boundary condition relaxation)法和方程延拓(equation continuation)法[5]。在均匀初始解中，求解域内部残差全部为零。在物面边界处，由于边界条件(无滑移或无穿透条件)的存在，会产生一个阶跃型非零残差。针对这一特点，边界松弛法通过逐步施加边界条件，降低迭代的不稳定性。Lyra[6]和Kuzmin[7-8]等对边界松弛法有较多的研究和应用。

在方程延拓法中，最为常见的就是经典的伪时间推进法(Pseudo Time Marching，PTM)。方程延拓法是指在控制方程中引入额外的项，得到性质改善的近似方程。然后逐次求解拓项系数不断减少的近似方程，逼近原方程的解。由于这种延拓处理不改变非线性迭代的起点和终点，所以此类延拓方法又被称为同伦延拓。伪时间推进法作为一种方程延拓法，在定常控制方程中引入了一个时间项，随着求解的收敛时间项的作用逐渐消失。对于隐式方法，伪时间项使控制方程雅可比矩阵的非奇异性和对角占优得到增强，保证了隐式迭代稳定性。作为一种经典方法，伪时间推进法得到了非常广泛的应用，也有很多研究和发展。Coffey等[9]提出了一种差分代数方程形式的时间推进法，提高了可压缩燃烧问题的收敛速度。Kelley等[10]提出了一种带约束的伪时间推进法，提高了迭代的稳定性。Ceze和Fidkowski[11-12]提出了一种针对非物理解的罚函数法，以提高伪时间推进法的鲁棒性，降低迭代发散的几率，从而提高计算效率。

在方程延拓法中，还有一类基于黏性或人工耗散的方法。这种方法在计算流体力学发展的早期就被用于定常流场的计算。Young等提出了用于加速全速势方程收敛的黏性松弛法[13]。Hicken等对比了黏性延拓和伪时间推进法在定常RANS方程求解中的效率和稳定性，认为“黏性延拓法”具有较高的鲁棒性和效率，是伪时间推进法的一种可能的替代方法”[14-15]。在计算流体力学领域以外，Pollock发表了一种针对线性对流输运方程的，通过拉普拉斯算子解决由于解中不光滑成分而导致病态雅可比的问题[16]。黏性延拓法中还有一种雷诺数延拓法[17]。这种方法非常便于实现，需要做的就是从一个较低的雷诺数开始定常迭代，这样较大的物理黏性会使问题具有足够的耗散从而保持稳定。根据Hicken和Zingg的研究结论[15]，这种方法存在一个不足，就是Navier-Stokes方程的物理黏性不涉及连续方程，所以增稳作用比较有限。

通常外流流场定常模拟的迭代过程就是把绕流物体的壁面边界对流动的影响传播到流场内部的过程。从这方面考虑，黏性延拓法有助于改善非线性求解部分的效率。然而，在牛顿迭代中，延拓项会对雅可比矩阵的性质产生直接影响，从这个角度看，伪时间法带来的较强的对角占优特性又相对更具有优势。为综合利用两者的优势，本文提出了一种拉普拉斯增稳伪时间推进(Laplacian stabilized Pseudo Time Marching, LPTM)法。通过引入拉普拉斯算子增加方程的稳定性，提高可用的CFL数，达到加速收敛、节约计算时间的目的。

本文首先介绍了控制方程和牛顿迭代法等工作基础，然后详细阐述了拉普拉斯增稳的迭代思路，分析其与经典伪时间推进法的优缺点，并给出了LTPM法的实现细节，最后，通过无黏NACA0012翼型、湍流RAE2822翼型和三维ONERA M6机翼3个算例，对LPTM法的收敛加速效果进行了验证。

1 控制方程及其隐式解法

本文计算采用格心格式有限体积法求解可压缩RANS方程，无黏通量通过三阶MUSCL重构的Roe格式计算[18]，无黏通量采用二阶中心格式离散[18],隐式时间推进中采用对称高斯-赛德尔(Symmetric Gauss-Seidel, SGS)迭代预处理的广义最小残差法(Generalized Minimal RESidual method，GMRES)求解线性子问题，并使用多重网格技术加速收敛。程序通过基于MPI的分布式并行策略提高计算速度。本文在计算中使用的湍流模型为SA(Spalart-Allmaras)一方程湍流模型[19]。

1.1 控制方程

本文所研究问题的控制方程是无量纲的定常可压缩RANS方程，表示为

(1)

式中：R(w)为残差，流体状态向量w=(ρ,U,p)，ρ、U和p分别为密度、速度和压力的流场自变量；F(w)和Fv(w)分别为无黏和黏性通量；Ω为求解域或控制体；v为积分变量。控制方程中的湍流黏性项需要通过求解湍流模型得到。在本文的讨论中，湍流模型的求解是和流动控制方程独立的。因此，本文不涉及关于湍流模型求解的问题。

1.2 伪时间推进法的基本作用

方程式(1)是关于w的非线性方程。在非线性迭代法中，牛顿迭代由于其二阶收敛能力而得到广泛应用。关于方程式(1)的牛顿迭代可以表示为

(2)

式中：n为迭代步数；R′为非线性算子的雅可比矩阵；δw为解向量w的增量。

但是牛顿迭代的收敛对方程的性质和初始解有较苛刻的要求：必须满足雅可比矩阵非奇异，初始解足够接近方程解。所谓“足够接近”，具体是指对于任意第n步牛顿迭代，须满足

(3)

式中：R″为非线性算子的海森矩阵；ε为当前解的误差。因此，增强牛顿迭代收敛性的一般思路是降低问题雅可比矩阵的奇异性，以及增强问题的线性。作为一种常见的特例，经典的全局化方法是伪时间推进法，通过引入伪时间项，所求问题转化为

(4)

式中：RPT(w)为包含伪时间项的总残差；Q(w)为守恒变量；τ为伪时间。

在实际计算中，Q(w)可以取为Navier-Stokes方程守恒变量，也可以简单取w本身。出于简化分析的考虑，本文取w。这样，牛顿迭代转化为

(5)

式中：dτ为伪时间步长。由于对角阵I的引入，所解问题的线性增强，式(4)中的雅可比矩阵在对角占优和条件数方面相对于式(2)有所改善，使牛顿迭代得以收敛。

2 拉普拉斯延拓

2.1 拉普拉斯算子的引入

1.2节提到，要保证牛顿迭代的收敛，基本策略就是降低雅可比矩阵的奇异性，增加问题的线性，使近似解尽快靠近问题真实解。要满足这些要求，伪时间推进法并不是唯一的选择。实际上，任意非奇异的线性算子，都能起到减少海森矩阵范数、增加雅可比矩阵范数的作用。因此，本文考虑引入另外一种线性算子——拉普拉斯算子作为延拓项。引入拉普拉斯项的控制方程如下：

(6)

式中：RLPT(w)为由流体状态向量w计算得到的残差；cLP为拉普拉斯项的缩放系数；Δ为拉普拉斯算子。这样，牛顿迭代公式变为

(7)

需要特别说明的一点是，在具体实现中，式(5)和式(7)的残差矢量都是由原始方程得到的，并不包含由延拓项产生的残差。根据作者的经验，这种选择得到的迭代格式比严格用牛顿迭代求解延拓后的方程具有更高的收敛效率。

另外，在黏性计算中，速度场在无滑移边界附近会形成边界层。此时，若对动量方程增加拉普拉斯算子，则会较大程度地扩散由无滑移边界条件引起的低速区，反而不利于收敛。因此，对于存在无滑移边界的问题，本文只对密度和压力等受诺依曼边界条件约束的分量施加拉普拉斯项。

2.2 拉普拉斯延拓作用

伪时间项向雅可比矩阵中加入了一个对角阵，拉普拉斯项在雅可比矩阵中引入了一个拉普拉斯算子。两者都是对称正定的线性算子，在改善控制方程正则性方面具有类似的作用。不过拉普拉斯逆算子与伪时间项逆算子相比，一个重要的特点是全局性。在实际计算中，数值解的误差以及雅可比矩阵和海森矩阵的范数都难以得到，延拓算子与方程本身复合后的逆算子的具体形式更是难以求出。因此，此处仅对拉普拉斯算子和伪时间项的区别做定性分析。

由于伪时间项是一个对角阵，对角阵的逆算子仍然是对角阵，显然它对残差矢量的响应是当地的、局部的。而拉普拉斯算子则不同。在三维欧氏空间中，通过格林函数法[20]可知，对于残差向量R(w(x))，在拉普拉斯逆算子作用下的响应为

(8)

这意味着任意一点的残差都会对解向量产生全局性的影响；同时任意一点的解向量变化，都包含了整个求解域中的残差信息。这正是拉普拉斯算子椭圆性的体现。考虑到定常流场求解通常初始化为均匀来流状态，初始残差仅在壁面处不为零，则在计算初始阶段，拉普拉斯算子向流场内部传递边界信息的效果要远远强于伪时间项，解的残差也就可以更快地降低。这样，由式(3)可知，牛顿迭代的稳定性也就更容易保证，对CFL数的要求也就可以放得更宽，最终可以通过使用较大的CFL数，得到更快的收敛速度。

但是，拉普拉斯延拓相对于伪时间推进法有2个方面的不足。第一，伪时间项在解逐步收敛时会自动消失，而拉普拉斯算子的作用在不加特殊处理的情况下会一直存在。这样，即使选用的较小的CFL数，其负面影响也只是局限于使收敛速度变慢，只要进行充分的迭代，仍能得到原始问题的解。这一特点给实际应用带来极大便利。而对于拉普拉斯延拓，必须特别设计一种机制，使得拉普拉斯项随迭代推进而消失。不过，这是个很容易克服的缺点。并且，在伪时间推进法中，为追求较高的收敛效率，通常也不会使用单一CFL数进行计算，同样涉及到在迭代过程中改变CFL数的问题。第二，正如式(8)所示，拉普拉斯算子的逆是具有全局影响的，反映在离散系统中，就意味其值对应的矩阵不再具有稀疏性。这样，基于近似LU分解的线性求解方法，包括ADI、LU-SGS以及本文使用的SGS方法，效率就会有所下降，从而导致线性问题求解的代价增加。在实际应用中，需要综合权衡拉普拉斯算子的正负作用，才能得到整体效率更优的求解策略。

2.3 迭代策略

本文的求解策略包含3层迭代。最外层是延拓迭代，随着迭代的进行，要保证延拓项不断降低。第2层是牛顿迭代，每个延拓方程仍然是一个非线性问题，本文通过牛顿迭代法进行求解。由于延拓问题不是最终关心的问题，所以牛顿迭代并不需要精确进行。本文针对每个延拓问题，只进行一步牛顿迭代。第3层迭代是针对牛顿迭代产生的线性问题，本文使用SGS预处理的GMRES方法进行求解。同样，由于牛顿迭代只是近似求解，线性求解同样也不需要严格进行。本文的策略是线性残差降低2个数量级时认为GMRES迭代收敛。

延拓项的推进策略使用成熟的CFL数递增策略(Switched Evolution Relaxation, SER)[21-22]。本文对cLP和CFL数的导数采用同样的递减模式，如式(9)所示。

(9)

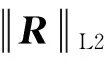
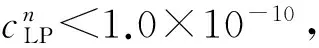
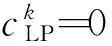
(10)

延拓参数的选择对计算的稳定性和效率有至关重要的影响。较大的延拓参数(对于时间推进法对应较小的CFL数)会使求解稳定但是收敛较慢，反之亦然。由于控制方程的非线性性质，对延拓参数数值的选择进行先验的理论分析较为困难，因此参数数值的选择具有一定的经验性。但是，这一问题在实际应用中是比较容易克服的。在气动外形优化工作中，通常需要对相似的计算状态进行数十、数百乃至上千次重复计算。在这种情况下，通过对目标状态进行数次试算，选取相对高效的CFL数和拉普拉斯项参数是完全可行的。

3 算例验证

3.1 计算效率的比较方法

本文通过计算收敛所消耗的CPU时间t衡量计算方法的效率。因此，首先需要保证计算硬件环境的一致。具体地，二维算例是在1个Intel Xeon E5-2 620 v3 2.40 GHz CPU上通过单进程计算，三维M6算例是在2个同样的CPU上通过10个MPI进程并行计算。其次要统一收敛判断标准。由于本文牛顿迭代所用的是近似雅可比矩阵，所以这里不追求控制方程非线性残差收敛到数值极限，而是以气动设计中常用的升力和阻力系数的收敛为标准。文献[23]指出一般工程问题对气动力的要求为：升力系数CL精确到0.001，阻力系数CD精确到0.000 1。本文采用上述容差的一半作为气动力收敛判断标准。具体地，针对最后10步非线性迭代，如果升力系数的变化范围小于0.5×10-3，并且阻力系数的变化范围小于0.5×10-4，则认为计算收敛。

(11)

需要说明的是，选取最后10步迭代作为观察范围是不具有一般性的，特别是在CFL比较小的计算中，很容易得到虚假收敛判定。因此，出于严谨性的考虑，对于本文所涉及的算例，在达到这一收敛判据后仅记录当时的CPU时间，计算迭代仍继续进行，后续的计算结果可以作为对收敛性进行人工辅助判断的依据。如果后续计算没有出现CL和CD的明显漂移或波动，则认为此收敛判定有效。实际结果表明，这一收敛判据对本文涉及的算例来说是合理准确的，以此为基础的计算效率对比也是有效的。

3.2 无黏NACA0012翼型

本算例考察了LPTM法对二维无黏问题的收敛加速作用。计算状态为来流马赫数0.8，迎角1.25°。计算网格总量为44 640单元，物面第一层网格高度为1.0×10-3，法向增长率为1.2。网格的大致结构和疏密分布如图1所示，Y/C和X/C分别为以弦长C无量纲化的纵、横坐标。

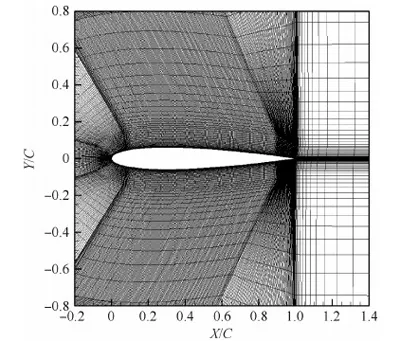
图1 无黏NACA0012翼型算例的计算网格

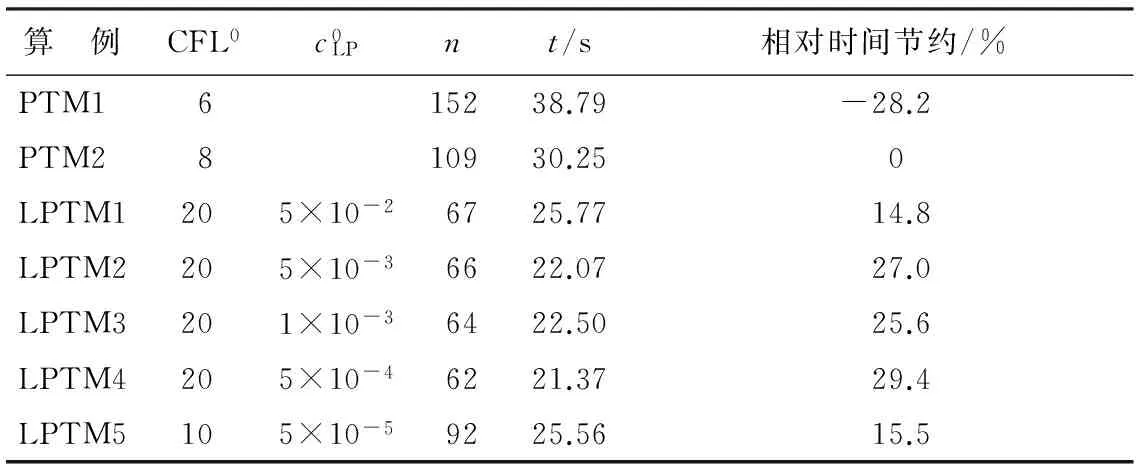
算 例CFL0c0LPnt/s相对时间节约/%PTM1615238.79-28.2PTM2810930.250LPTM1205×10-26725.7714.8LPTM2205×10-36622.0727.0LPTM3201×10-36422.5025.6LPTM4205×10-46221.3729.4LPTM5105×10-59225.5615.5

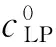
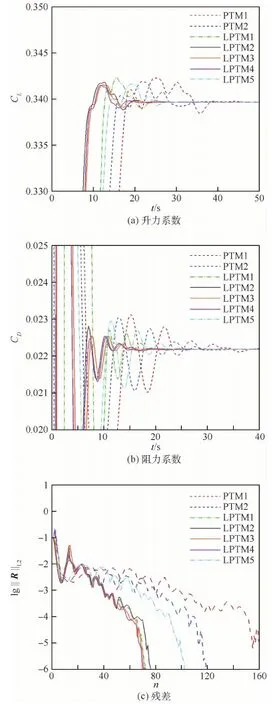
图2 无黏NACA0012翼型算例升力系数、阻力系数及残差收敛曲线

图2(a)、(b)给出了无黏NACA0012翼型算例升力系数和阻力系数对计算CPU时间的收敛曲线。可以看出LPTM法的力系数收敛有明显的提前，并且振荡的幅度也有所降低。图2(c)给出了系统残差随迭代步数的收敛过程。由图2可见，收敛曲线依CFL数分为4簇，显示了CFL数对收敛效率具有直接决定性作用。而LPTM算例之所以能使用更高的CFL数，原因是拉普拉斯算子的引入。在最初的几步迭代中，拉普拉斯算子的引入可以使残差更快收敛，验证了2.2节中对拉普拉斯项作用的分析。

图3给出了本文计算得到的翼型压力分布与Vassberg和Jameson[24]通过4 096×4 096规模的网格得到的压力分布的对比，Cp为压力系数。由于各计算结果收敛较为一致，为清晰起见，图中只给出了LPTM法与PTM法各一个结果，并未逐一对比。从图中可见，LPTM法与PTM法得到的计算结果有较高的一致性，并且与参考结果符合较好。这表明，本文LPTM法并没有因为提高计算效率而牺牲精度。

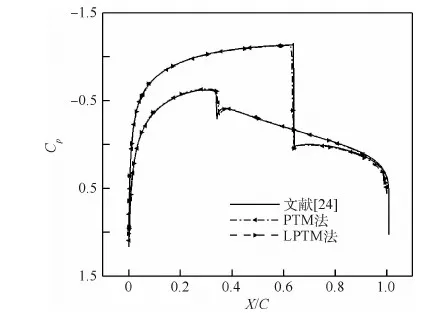
图3 无黏NACA0012翼型算例的表面压力系数分布

3.3 湍流RAE2822翼型

本算例考察了LPTM法对二维湍流问题的收敛加速作用。计算算例采用AGARD-AR-138报告中湍流RAE2822翼型实验[25]的Case10。实验来流马赫数0.75，基于弦长的雷诺数6.2×106，实验迎角3.19°，升力系数0.743。计算时为匹配实验升力系数，将迎角修正为3.09°。计算网格总量为58 720单元，物面第一层网格高度为1.0×10-5，法向增长率为1.2，平均y+为0.9。网格的大致结构和疏密分布如图 4所示。

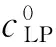
图5(a)、(b)给出了本算例升力系数和阻力系数的收敛过程。比较值得注意的一点是，从收敛历程的形态上看，在cLP较小时，收敛过程似乎只是由于CFL数较大而被压缩了。而当cLP较大时，收敛过程的形态也发生了变化，这意味着拉普拉斯算子的存在改变了迭代过程在解空间的路径。图5(c)给出了本算例系统残差随迭代步数变化的过程。在迭代初始阶段，CFL数相同的LPTM1～4算例，较大cLP的算例残差收敛速度较快，直接体现了拉普拉斯算子的作用。而整体收敛历史同样以CFL数分为4簇，体现了CFL数对收敛效率的重要影响，以及通过拉普拉斯延拓增加可用CFL数的意义。

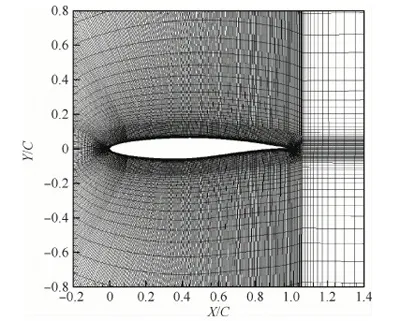
图4 湍流RAE2822翼型算例的计算网格

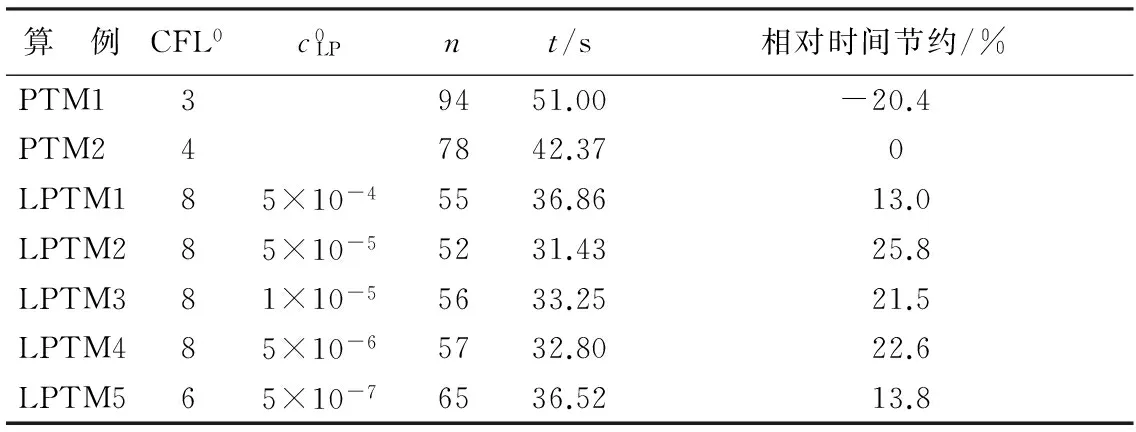
算 例CFL0c0LPnt/s相对时间节约/%PTM139451.00-20.4PTM247842.370LPTM185×10-45536.8613.0LPTM285×10-55231.4325.8LPTM381×10-55633.2521.5LPTM485×10-65732.8022.6LPTM565×10-76536.5213.8

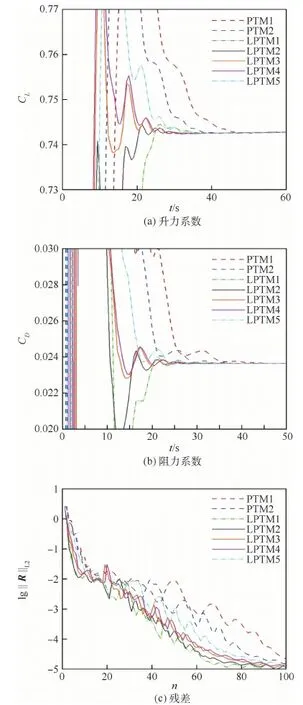
图5 湍流RAE2822翼型算例升力系数、阻力系数及残差收敛曲线

图6给出了本算例得到的表面压力系数分布。可以看出，计算结果与实验结果符合较好，并且LPTM法与经典的PTM法得到的压力分布有较高的一致性。

3.4 三维ONERA M6机翼

本算例通过ONERA M6[26]算例来测试LPTM法在三维黏性计算中的表现。计算状态为来流马赫数0.839 5，基于参考弦长Cref=0.646 1 m的雷诺数为1.172×107，迎角3.06°。相对于前2个算例，本算例雷诺数更高，因此物面第一层网格尺度更小，数值离散后的控制方程稳定性问题更为突出。本算例计算所用湍流模型仍为SA模型。计算网格5 997 680单元，物面第一层网格法向高度为2.0×10-6，法向增长率为1.2，平均y+为1.2。网格的大致结构和疏密分布如图7所示。

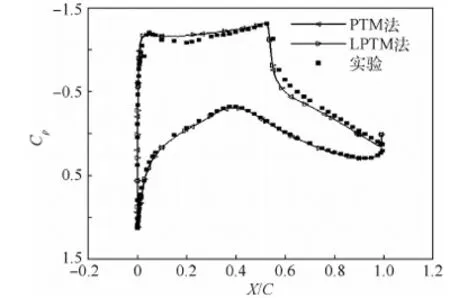
图6 湍流RAE2822翼型算例的表面压力系数分布

图7 三维ONERA M6机翼算例的计算网格

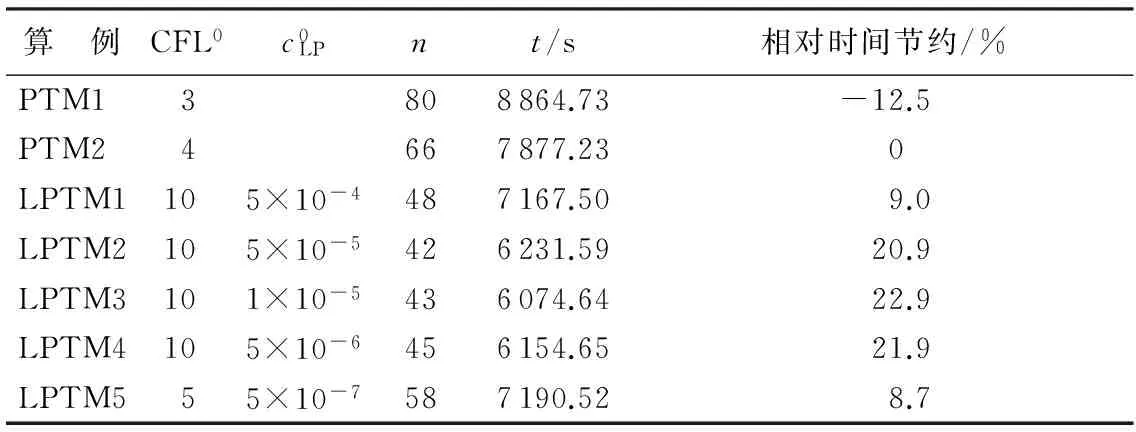
算 例CFL0c0LPnt/s相对时间节约/%PTM13808864.73-12.5PTM24667877.230LPTM1105×10-4487167.509.0LPTM2105×10-5426231.5920.9LPTM3101×10-5436074.6422.9LPTM4105×10-6456154.6521.9LPTM555×10-7587190.528.7

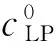
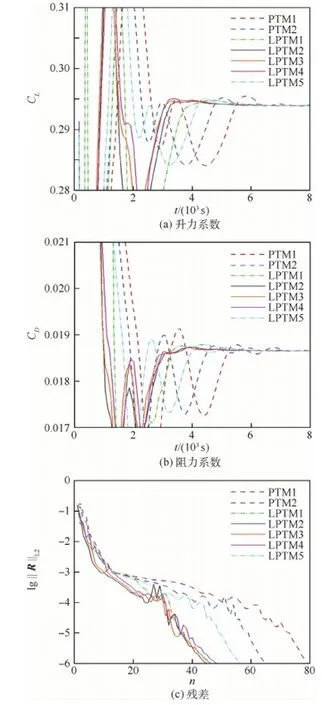
图8 三维ONERA M6机翼算例升力系数、阻力系数及残差收敛曲线

图8(a)、(b)给出了本算例升力系数和阻力系数的收敛曲线，可见不同cLP值对力系数收敛的加速效果。图8(c)给出了本算例残差随迭代步数的收敛历史，收敛曲线同样依CFL数分为4簇。在迭代初期，引入拉普拉斯延拓的算例同样显示了较快的收敛速度。图9给出了本文计算得到的表面压力分布与实验结果的对比，y/b为截面展向站位。可以看出，计算结果与实验结果符合较好，并且LPTM法与经典的PTM法得到的压力分布有较高的一致性。

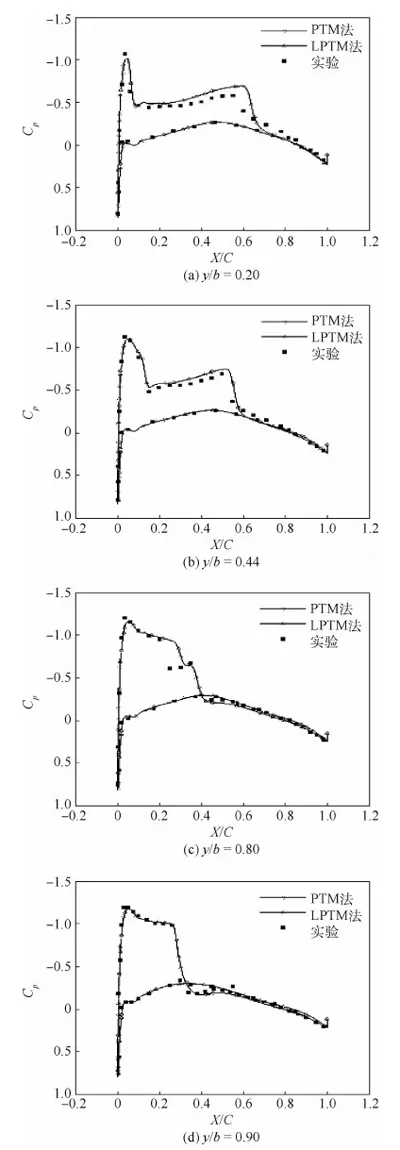
图9 三维ONERA M6机翼算例表面压力系数分布

4 结 论

为提高速定常流动模拟的计算效率，构造了一种在经典伪时间推进法基础上附加一个拉普拉斯项的混合延拓方法。

1) 在常规的伪时间推进法中，伪时间项作为延拓项，通过增强控制方程的线性以及改善雅可比矩阵的对角占优实现了牛顿迭代的稳定化。拉普拉斯算子是一个对称正定的线性椭圆算子，不仅与伪时间项同样有增强方程正则性的作用，还有提供耗散、加速边界信息向流场内部传播的作用。综合利用拉普拉斯算子和伪时间项各自的优势可以构造效率更高的计算方法。

2) 拉普拉斯延拓法对收敛效率的实际影响与迭代参数的选择有密切关系。本文通过数值实验，总结得到了计算效率较优的一个拉普拉斯项参数平台区，可以作为在实际问题中应用本文方法的一个参考。具体地，通过无黏NACA0012翼型、湍流RAE2822翼型和三维ONERA M6机翼等3个算例，验证了拉普拉斯延拓方法分别在有黏/无黏、二维/三维对定常流动求解的加速效果。计算结果表明，拉普拉斯延拓法可以节省20%以上的计算时间，在迭代过程中引入拉普拉斯算子作为加速收敛措施，是有实际应用价值的。此外，即使选定相对次优的拉普拉斯参数时，本文方法仍能起到部分加速作用，而不至于完全失效或起到负效果，证明本文方法在实际应用中足够的鲁棒性。

参考文献(References)

[1] GEUZAINE P.Newton-Krylov strategy for compressible turbulent flows on unstructured meshes[J].AIAA Journal,2001,39(3):528-531.

[2] WONG J S,DARMOFAL D L,PERAIRE J.The solution of the compressible Euler equations at low mach numbers using a stabilized finite element algorithm[J].Computer Methods in Applied Mechanics and Engineering,2001,190(43-44):5719-5737.

[3] DENNIS J,SCHNABEL R.Numerical methods for unconstrained optimization and nonlinear equations[M].Philadelphia:Society for Industrial and Applied Mathematics,1996：116-126.

[4] MICHALAK C,OLLIVIER-GOOCH C.Globalized matrix-explicit Newton-GMRES for the high-order accurate solution of the euler equations[J].Computers & Fluids,2010,39(7):1156-1167.

[5] BROWN D A,ZINGG D W.Advances in homotopy continuation methods in computational fluid dynamics:AIAA-2013-2944[R].Reston:AIAA,2013.

[6] LYRA P R M,MORGAN K.A review and comparative study of upwind biased schemes for compressible flow computation.PartⅢ:Multidimensional extension on unstructured grids[J].Archives of Computational Methods in Engineering,2002,9(3):207-256.

[7] KUZMIN D,LOHNER R,TUREK S.Flux-corrected transport:Principles,algorithms,and applications[M].2nd ed.Berlin:Springer,2012:193-238.

[8] KUZMIN D,LOHNER R,TUREK S.Flux-corrected transport:Principles,algorithms,and applications[M].Berlin:Springer,2005:207-250.

[9] COFFEY T S,KELLEY C T,KEYES D E.Pseudotransient continuation and differential-algebraic equations[J].SIAM Journal on Scientific Computing,2003,25(2):553-569.

[10] KELLEY C T,LIAO L Z,QI L,et al.Projected pseudotransient continuation[J].SIAM Journal on Numerical Analysis,2008,46(6):3071-3083.

[11] CEZE M,FIDKOWSKI K J.A robust adaptive solution strategy for high-order implicit CFD solvers:AIAA-2011-3696[R].Reston:AIAA,2011.

[12] CEZE M,FIDKOWSKI K J.Constrained pseudo-transient continuation[J].International Journal for Numerical Methods in Engineering,2015,102(11):1683-1703.

[13] YOUNG D P,MELVIN R G,BIETERMAN M B,et al.Global convergence of inexact Newton methods for transonic flow[J].International Journal for Numerical Methods in Fluids,1990,11(8):1075-1095.

[14] HICKEN J,BUCKLEY H,OSUSKY M,et al.Dissipation-based continuation:A globalization for inexact-Newton solvers:AIAA-2011-3237[R].Reston:AIAA,2011.

[15] HICKEN J,ZINGG D.Globalization strategies for inexact-Newton solvers:AIAA-2009-4139[R].Reston:AIAA,2009.

[16] POLLOCK S.A regularized Newton-like method for nonlinear PDE[J].Numerical Functional Analysis and Optimization,2015,36(11):1493-1511.

[17] KNOLL D A,KEYES D E.Jacobian-free Newton-Krylov methods:A survey of approaches and applications[J].Journal of Computational Physics,2004,193(2):357-397.

[18] BLAZEK J.Computational fluid dynamics:Principles and applications[M].2nd ed. Oxford:Elsevier Science,2005:227-270.

[19] SPALART P R,ALLMARAS S R.A one-equatlon turbulence model for aerodynamic flows:AIAA-1992-0439[R].Reston:AIAA,1992.

[20] POLYANIN A D,NAZAIKINSKII V E.Handbook of linear partial differential equations for engineers and scientists[M].2nd ed.Boca Raton:Chapman and Hall/CRC,2015:1199-1231.

[21] CEZE M,FIDKOWSKI K.Pseudo-transient continuation,solution update methods,and CFL strategies for DG discretizations of the RANS-SA equations:AIAA-2013-2686[R].Reston:AIAA,2013.

[22] MULDER W A,LEER B V.Experiments with implicit upwind methods for the euler equations[J].Journal of Computational Physics,1985,59(2):232-246.

[23] 张涵信.关于CFD高精度保真的数值模拟研究[J].空气动力学学报,2016,34(1):1-4.

ZHANG H X.Investigation on fidelity of high order accuate numerical simulation for computational fluid dynamics[J].Acta Aerodynamica Sinica,2016,34(1):1-4 (in Chinese).

[24] VASSBERG J,JAMESON A.In pursuit of grid convergence,Part I:Two-dimensional Euler solutions:AIAA-2009-4114[R].Reston:AIAA,2009.

[25] COOK P H,MCDONALD M A,FIRMIN M C P.Aerofoil RAE2822—Pressure distribution and boundary layer and wake measurements:AGARD-AR-138[R].Reston:AGARD,1979.

[26] SCHMITT V,CHARPIN F.Pressure distributions on the ONERA-M6-wing at transonic mach numbers:AGARD-AR-138[R].Reston:AGARD,1979.