Black—Litterman模型与同等权量组合(equal—weight portfolio):哪个更好?
何思源 DH1 3LE
Black-litterman模型 同等权量组合 (equal-weight portfolio)
引言
长期以来,关于最优组合和同等权量组合的比较的争论一直存在。很长一段时间内,平均数方差(MV)最优组合在资产分配中占据着重要地位,该模型提供给投资者组合收益的平均数和方差。然而,由于其相对于单纯的多样化的较差的表现,一些学者开始质疑该模型。本文首先会评估两篇文献对于最优组合和1/N策略(即同等权量组合)的比较,其次会重点关注Black-Litterman模型的表现(此模型可以被归为Bayesian模型),并进一步与多样化策略和实施该模型的原始文章作比较。
文献的简要综述
DeMiguel,Garlappi和Uppal(2009)进行了关于14个不同的样本外组合模型的表现与基于七个实际的每月回报数据集合的单纯多样化模型的比较。根据七个实验数据集合得出的结果,任何一个最优模型都没有1/N策略的表现优异,因为1/N模型中有最高的夏普比率值和CEQ值并且只有同等价值的市场模型的流通量大于1/N的流通量。1/N策略之所以比其他模型在给定的数据集中有较好表现的原因有两点:1/N策略中的权衡误差比其他模型中要小;1/N模型是用来分散股票组合的价值而不是单独股票的价值,这就降低了组合中特定的波动性。在评估了14个模型之后,三位学者得出了结论:通过比较夏普比率,CEQ值和流通量以后,没有一个模型比1/N策略表现更优异。当分析决定性的估计窗口时,仅仅包含25种资产的一个组合需要选取30000个月的数据,依据美国股票市场调整的数据参数得出,一个含有50中资产的组合应该选取超过5000个月的数据;然而,只需要60个月到120个月之间的来估计这些造成1/N策略优于平均数方差的组合的参数。对于有估计误差的无限制策略,他们要差于有限制策略和1/N策略,这也就意味着基于样本时,将模型予以限制会提高最优组合的表现。限制只在提高较小的估计窗口的表现起作用,反之亦然;可是,这些模型就算加以限制也没有1/N策略更优。
Black和LiRerman(1992)的模型(BL)是可以与最优组合替换的,可是却很少在以往的文献中讨论,所以该模型的合理性以及其表现就是未知的。但是,Bessler,Opfer和Wolff(2014)试图将经验数据运用于多资本组合中来探究样本外的BL模型的表现,然后比较优化模型(三种类型的Black-Litterman模型:作为参考组合的战略权重的BL模型,作为参考组合的含有1/N的BL模型和作为参考组合的含有最小值方差的BL模型;平均数方差,最小值方差和Bayes-Stein收缩组合)和单纯的多样化策略。
Bessler,Opfer和Wolff(2014)的发现可以在完整样本和不同的市场环境中分析。根据完整样本中的结果,三个BL模型相比于其他四个与保守的,有节制的和有进取性的投资者有关的模型,有着高Omega和夏普比率,这就表明BL模型优于单纯的多样化组合。BL组合比平均值方差和Bayes-Stein规则既有较低的风险和较低的最大跌幅,也有最小流通量和交易成本。考虑最优组合在不同市场环境的表现时,整个时期可以分为四个子时段:第一时期是从1993年一月份到2001年一月份并定义为扩展期;第二时期是从2001年二月份到2004年六月份,共涵盖41个月,定义为衰退期;第三时期是从2004年七月份到2008年二月份,包括44个月,这个时期包含了高利率和牛市市场;第四时期是从2008年3月份到2011年12月份,包括46个月以及金融风险。BL组合在这个时期都优于其他四个模型,因为其有着较高的夏普利率,较低的风险,较低的组合流通量,较低的交易成本和多样化的资本类别。
实证分析
本文复制了Bessler,Opfer和Wolff(2014)中的Black-Litterman模型,但是是基于不同的数据集合(包括了25 Fama-French组合回报和因素组合)和不同的时期(从1976年1月份到2015年12月份);同时采用夏普比率来衡量BL模型。根据原始文獻,BL模型的简要解释是:投资者应该给予未来回报合理的估计仅仅是为了与可能是市场或是基准组合分离开。BL模型包含了隐含回报(通过CAPM模型计算出的优先的预期回报)和主观回报估计(可以定义为获得较后的预期回报的见解)。本文采用了原文献的关于测量主观回报估计的方法:将样本平均数看作是投资者的见解。BL模型也考虑了估计的可信度,该可信度可以表示为矩阵Q。本文使用了Meucci(2010)建立的Q的简单公式,该公式基于假设:见解的合理性是与隐含回报的合理性成比例的。
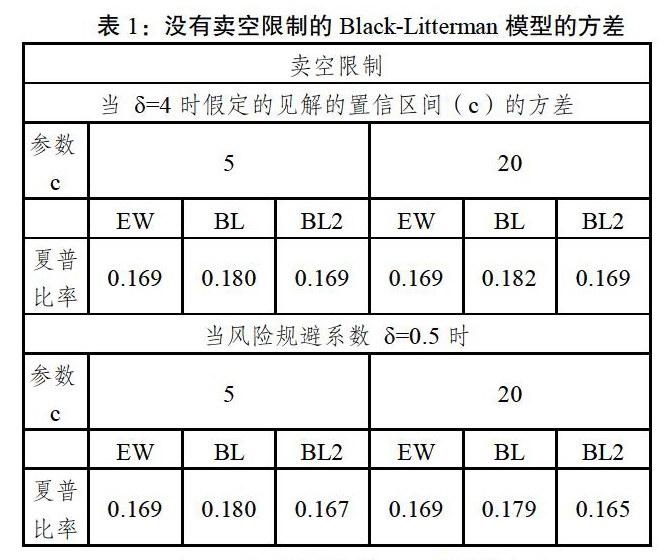
为了探究结果是否对方差和限制敏感,本文首先考虑有或者没有卖空限制的情况,然后在确定τ为0.05不变的时候,改变见解的置信区间(c)和风险规避系数(6)。交易成本对于BL模型的影响也被考虑其中,文章也给出了没有考虑交易成本的BL模型(BL)和考虑交易成本的BL模型(BL2)的结果。表1中,当风险规避系数从0.5增长到4的时候,BL模型表现有提升,这意味着在BL模型中厌恶风险的投资者有较高的预期回报,因为他们倾向于投资能给他们固定回报的资产;同时其也在较小的置信区间中表现优异,因为当置信区间(c)较小时Q较大并且基于历史估计误差的回报预测的见解估计更可信。BL模型的确受到了交易成本的影响,但是它还是优于同等权量组合,该发现是与原始文献相同的。表2中,考虑交易成本的BL模型表现差于没有考虑卖空限制时的模型。这些模型和同等权量组合表现相同,有些甚至没有1/N策略表现得好,但是,这个结论是与原文献有冲突的,因为原文献表示BL模型表现有所提高,甚至要优于1/N策略。该差异之所以存在是因为原文献包含了由股票,债券和商品指数的多资产组合,本文只考虑了股票,并且两篇文章使用的数据集合是不同的。
结论
本文参照了Bessler,Opfer and Wolff(2014)中的Black-Litterman模型,建立了基于样本的BL模型,并且在从1976年1月份到2012年12月份的25Fama-French组合回报和因素组合的基础上比较BL模型与同等权重组合。没有卖空限制的BL模型的表现与原文献中相同,但是存在卖空限制的BL模型却差于原文献中的该模型。在原文献中,BL模型相较于同等权量组合有着优异的样本外的表现;然而,在本文中,BL模型在有卖空限制的时候甚至要优于1/N策略。这个差异的存在原因可能是不同的资产分配,意味着原始文献考虑的是包含了债券,商品指数和国际股票的多资本组合,但是本文仅仅考虑了股票。当只投资于股票市场时,分散化投资的影响相对较小而且交易成本的影响与估计误差大于重新分配组合的收益,这就导致同等权量组合优于最优组合。当回报的估计值更准确,资产的选择更广泛的时候,最优组合优于单纯的多样化策略。总而言之,Black-Litterman模型在大多数情况综述优于同等权量组合。