花椒真空干燥特性分析及动力学模型研究
孟国栋,彭桂兰,罗传伟,黎斌,杨玲, 张雪峰
(西南大学 工程技术学院,重庆,400715)
花椒(Zanthoxylumbungeanum)作为一种传统调味品,是中国大众不可或缺的食用原材料之一。日常食用的花椒为青椒或花椒的干燥成熟果皮[1]。新鲜花椒采收后含水率高,在贮藏过程中极易受外界条件的影响,发生质变。干燥是花椒收获后重要的处理环节,对花椒的运输、贮藏起到重要作用。传统的干燥方式存在干燥效率低、干燥品质差等缺点,而真空干燥是一种新型热门的干燥技术,具有节能、环保、干燥品质好等优点[2],目前已得到广泛应用[3-9]。
通过绘制干燥特性曲线可以对花椒的真空干燥过程进行直观分析,同时建立干燥动力学特性数学模型能够较准确地预测干燥过程中水分变化规律。Lewis在1921年提出了干燥理论,并建立了Lewis模型。后来世界各国学者在此干燥理论基础上研究出了更多的干燥理论及模型,并对各种物料的干燥过程进行了建模分析,为干燥理论的研究和发展奠定了基础[10-13]。
本文通过真空干燥技术,选取干燥温度为50、60、70 ℃;真空度为-0.06、-0.04、-0.02 MPa;装载量为30、40、50 g进行3因素3水平的全面试验。利用7种经典干燥数学模型拟合试验数据,并选取其最优模型和BP神经网络模型进行对比,得到花椒真空干燥最佳数学模型。以期能够较准确地预测花椒真空干燥过程中水分变化规律,为花椒的真空干燥工艺提供指导。
1 材料与方法
1.1 材料
新鲜花椒(江津九叶青),2016年9月购置于北碚区农贸市场。
1.2 设备
智能型温度控制器DZF型电热真空干燥箱,北京科伟永兴仪器有限公司;电子天平(METILER TOLEDO AL204),上海梅特勒-托利仪器有限公司,精度0.000 1 g;KW-2型旋片式真空泵,北京科伟永兴仪器有限公司;直径100 mm的筛网9只,规格1 mm(用于承载花椒);自封袋若干,规格10 cm×15 cm(用于贮存花椒干燥样本);滤纸若干,用于吸除花椒表面多余水分。
1.3 花椒真空干燥工艺流程
新鲜花椒→洗净(除泥污)→除杂(叶、梗)→筛选(除去干瘪、霉烂、破损个体)→除去表面水分→干燥→封装
1.4 试验方法与设计
实验前将试验用筛网放入真空干燥机进行预热,减小热惯性对花椒干燥造成的影响,选取筛选后大小均匀的新鲜花椒并用滤纸吸除表面多余水分放置在大筛网上备用。根据前期干燥预实验,选取干燥温度为50、60、70 ℃,真空度为-0.06、-0.04、-0.02 MPa,载重量为30、40、50 g。每隔20 min称重记录实时数据,直到含水率下降到11%.d.b左右停止试验[14]。每组进行3次平行试验。
1.5 指标测定与方法
(1)花椒初始含水率测定参照GB5009.3—2010[15]。
(2)含水率比(MR)

(1)
式中:We,试样平衡含水率,%d.b.;W0,试样初始含水率,%d.b.;Wt,试样在t时刻的含水率,%d.b.
(3)干燥速率(DR):

(2)
式中:Mt,试样在t时刻的含水率,Mt+Δt,试样在t+Δt时刻的含水率,%.d.b;Δt,时间差值,min。
(4)试验评价指标
根据国内外学者在研究干燥试验中选用的评价指标评判模型拟合度的经验[16-17]。本试验选用决定系数R2、残差平方和(SSE)、卡方χ2以及平均相对误差E作为评价指标。其计算式如下:

(3)

(4)

(5)

(6)

1.6 BP神经网络设计
(1)输入层和输出层节点的确定:影响花椒真空干燥试验的3个因素分别为温度、真空度和装载量,而试验目标参数水分比随时间发生变化,因此选择这4个因素作为输入节点。输出层与试验的目标参数水分比一致,因此将水分比作为输出层节点,且输出数据的范围是[0,+1]。
(2)隐含层节点数的确定:根据经验公式可以进行隐含层节点数的选择[18]。经验公式如下:

(7)
式中:m为隐含层节点数;a为输入节点数;b为输出节点数;n为1~10之间的调节常数。
在本文中,a=4,b=1。则依据公式(7)可得3 (3)传递函数及算法:选择trainlm作为训练函数,Tansig作为输出层的传递函数。与传统BP算法相比,Levenberg-Marquardt算法梯度下降更快,在整个网络的收敛上能以很少的迭代次数达到误差要求。因此采用Levenberg-Marquardt算法进行训练。 将花椒真空干燥全面试验中的25组作为训练样本剩余2组作为测试样本,通过BP神经网络对训练样本进行训练,再将测试样本进行检验最后输出结果。 为了使数据具有统一性,对试验因子的参数进行归一化处理,本文采用如下公式进行归一化处理: (8) 式中:xi为归一化处理后的数据;x为试验数据;xmin为原始数据中最小值;xmax为原始数据中的最大值。 利用Microsoft Excel软件进行数据记录和计算,数据的分析和作图通过Oringin Pro 8.0和Matlab 2014a实现。 2.1.1 温度对干燥特性的影响 在装载量为50 g、真空度为-0.04 MPa的条件下,控制干燥温度分别为50、60、70 ℃,研究温度因素对花椒真空干燥特性的影响。其干燥特性曲线如图1所示。 由图1干燥特性曲线可以看出,温度对花椒的干燥影响特别显著。50、60、70 ℃条件下达到安全含水率11%.d.b左右的时间分别为1 100、680、500 min,其最大干燥速率分别为0.306 6、0.513 6、0.541 3%/min,平均干燥速率分别为0.176 6、0.323 5%/min、0.397 9%/min。干燥温度越高形成的温度梯度越大,使得花椒表面存在的自由水急剧向干燥室中扩散,花椒表面自由水逐渐减少,与内部形成一定的湿度梯度[20]。与此同时,干燥室温度开始逐渐向花椒内部传递,花椒内部温度升高,在温度梯度和湿度梯度的共同作用下干燥速率达到最大值,从50 ℃升高到60 ℃时,干燥至安全含水率所用干燥时间缩短了420 min;从60 ℃升高至70 ℃干燥时间缩短了180 min。可见且随着温度的升高,相同温度梯度的影响程度逐渐减小。 图1 不同温度条件下花椒真空干燥特性曲线 2.1.2 真空度对干燥特性的影响 在装载量为40 g、温度为50 ℃的条件下,控制真空度分别为-0.02、-0.04、-0.06 MPa进行试验,研究真空度因素对花椒真空干燥特性的影响。其干燥特性曲线如图2所示。 由图2干燥特性曲线可以看出,真空度对花椒的干燥有一定的影响。降低气压可以降低水的沸点,随着真空度的升高,干燥时间也随之缩短,真空度为-0.02、-0.04、-0.06 MPa时所对应的干燥时间分别为1 100、980和960 min。其最大干燥速率分别为0.246 3、0.346 9、0.384 3%/min,平均干燥速率分别为1.688、0.200 5、0.211 6%/min。干燥前期升速阶段明显,没有恒速干燥期,降速阶段占整个干燥时间的90%以上,是典型的降速干燥过程。 图2 不同真空度下花椒真空干燥特性曲线 2.1.3 装载量对干燥特性的影响 在温度为60 ℃,真空度为-0.06 MPa的条件下,分别控制装载量为30、40、50 g进行试验,研究装载量因素对花椒真空干燥特性的影响。其干燥特性曲线如图3所示。 图3 不同装载量条件下花椒真空干燥特性曲线 由图3干燥特性曲线可以看出,装载量对花椒真空干燥有一定的影响。花椒干燥至安全含水率所用的时间与载重量呈正相关,这主要是因为花椒干燥存在着一个内部水分向表面迁移的过程,装载量越大迁移路径越长,所用的干燥时间也就越长。30、40、50 g时干燥至安全含水率所需的时间分别为480、600、700 min,对应的最大干燥速率分别为0.554 9、0.384 3、0.190 5%/min,平均干燥速率分别为0.310 7、0.232 3、0.202 1%/min。当载重量为30 g时,干燥至安全含水率所用的时间比载重量为40 g干燥至安全含水率时所用的时间快0.4倍,比载重量为50 g时要快0.94倍。 本研究选取载重量为30 g的9组试验通过Oringin 8.0运用表1中的7种经典数学模型进行非线性拟合,并利用R2、SSE、χ2三个指标对模型的拟合程度进行综合评价(见表2)。 由表2所列数据可以看出三次多项式模型的决定系数R2值均达到0.999,高于其他6种模型的R2值;SSE为残差平方和表示随机误差效应,其值越小拟合度越好。三次多项式模型的SSE值最低达到了0.000 7,且最高值也仅为0.001 1,所以三次多项式模型相较于其他6种数学模型数据离散程度更低,因此拟合效果更好。为确定适合花椒真空干燥的最佳数学模型,需进一步作卡方检验,卡方(χ2)是检验相关性的重要指标,值越小,则相关性越高。三次多项式模型卡方最小值是在50 ℃、-0.06 MPa、30 g试验条件下取得,此时卡方值为3.08E-5,均低于其他6种模型的χ2值,因此三次多项式模型比其他6种数学模型在描述花椒真空干燥水分比变化过程时更具有相关性。 表1 干燥数学模型及表达式Table 1 Drying models and equations 注:式中k、a、b、c、d、n均为未知参数。 表2 数学模型相关参数及评价指标Table 2 Relevant parameters and evaluation index of the mathematical model 续表2 综上分析,三次多项式模型是以上7种经典干燥数学模型中描述花椒真空干燥动力学特性的最佳模型。 将各个试验点的数据按照式(8)作归一化处理。根据公式(7)可知该神经网络隐含层节点数为4~13个,本文选取25个试验组的896个数据作为训练数据进行隐含层节点选取。经过神经网络工具箱进行训练,结果如表3所示。 表3 不同隐含层节点训练结果Table 3 The training results based on variationalhidden-layer nodes 理论上已经证明:在不限制隐含层节点数的情况下,只有一个隐含层的BP 网络可以实现任意非线性映射。通过表3可知,试验中当隐含层节点数为10时,所对应的误差最小,模型拟合效果最好,所以本文隐含层的神经元数选择为10个。该神经网络的隐含层为1层,隐含层节点数为10个,输出层为1层。由此确定了该BP神经网络模型的拓扑结构如图4所示。 图4 花椒真空干燥BP神经网络拓扑结构 运用BP神经网络工具箱对花椒真空干燥27组试验中的25组试验的896个数据进行训练。由图5可知经过352次训练后网络误差值达到稳定要求,并且在346次训练后达到最优值0.021 986。 图5 BP神经网络模型训练结果 由BP神经网络模型的训练与检验R值拟合结果可知(见图6),此条件下模型的训练R值达到0.998 89,检验R值达到0.998 87,模型拟合度好,干燥特性曲线值预测可信度高。 图6 BP神经网络模型训练与检验R值拟合结果 花椒真空干燥的BP神经网络权矩阵为: w(1,1)= w(2,1)=[-4.563 4.544 6 -14.563 4 4.476 8 -4.641 18.691 2 -7.361 3 -7.267 5.912 6 13.119 1] 阈值向量为: b(1)=[-4.444 3;-6.176 6;0.734 29;0.249 3; 0.134 56;0.562 16;5.571 6;3.14;-4.560 6;6.217 7] b(2)=[4.35] 利用工艺参数为:70 ℃、-0.04 MPa、50 g的实验组对三次多项式模型和BP神经网络模型进行拟合检验,结果如图7所示。 图7 三次多项式模型和BP神经网络模型的检验拟合曲线 此条件下得到的三次多项式模型为:MR=1.368E-9t3-3.50E-6t2-3.615E-4t+0.994,根据方程计算出拟合值,此时三次多项式模型平均相对误差E值为1.98%,在400 min以后预测值与试验测量值的偏差开始变大。将该组实验数据通过已训练好的神经网络模型进行拟合检验,结果表明BP神经网络模型平均相对误差E值为1.13%,2个模型的平均相对误差值都很小,但是BP神经网络模型平均相对误差值更小,拟合曲线与实际值几乎完全重合。综上所述,BP神经网络模型为描述花椒真空干燥动力学特性的最佳模型。 通过花椒真空干燥特性分析可知,平均干燥速率与干燥温度、真空度成正比,与装载量成反比这与车刚等[21]在蕨菜真空干燥试验研究中的结论相符。并且温度对花椒干燥时间影响最显著,温度越高干燥时间越短,真空度对干燥时间影响不明显这一结果在刘云宏等[22]的金银花真空干燥试验研究中得到相同的印证。花椒真空干燥是典型的降速干燥过程,没有恒速干燥期这与尹慧敏等[23]在马铃薯热风干燥试验研究报道中的结论一致。 通过7种经典干燥数学模型对9组实验数据进行非线性拟合,利用决定系数R2、残差平方和(SSE)、卡方χ2三个指标对拟合结果进行评价,结果表明三次多项式是7种经典干燥模型中描述花椒真空干燥动力学特性的最优数学模型,而在李辉等[24]的荔枝果肉微波真空干燥实验研究中发现Henderson and Pabis模型是描述其干燥动力学特性的最优模型;刘云宏等[25]和黄艳等[26]分别在地黄、银耳微波真空干燥试验中发现Page模型是描述其干燥动力学特性的最优模型,这可能与干燥方式和物料品性有关。 通过建立BP神经网络模型,对花椒干燥过程进行预测。对25组试验数据进行352次训练得到花椒干燥BP神经网络模型。最终将三次多项式与BP神经网络模型进行对比检验,结果显示两者的拟合平均相对误差值分别为1.98%和1.13%。因此BP神经网络是更适合描述花椒干燥动力学特性的数学模型,这与黎斌等[27]在魔芋真空干燥研究中的结论一致。1.7 试验数据处理

2 结果与分析
2.1 真空干燥因素对花椒干燥特性的影响

Fig.1 Vacuum drying curve of Zanthoxylum bungeanum under different temperature conditions
Fig.2 Vacuum drying curves of Zanthoxylum bungeanum under different vacuum degree
Fig.3 Vacuum drying curve of Zanthoxylum bungeanum under different loading conditions2.2 模型拟合及检验



2.3 BP神经网络模型建立


Fig.4 The topological structure of BP neural network for the Zanthoxylum bungeanum vacuum drying
Fig.5 results of BP neural network model training
Fig.6 BP neural network model training and test R value fitting results
2.4 三次多项式和BP神经网络模型的对比检验
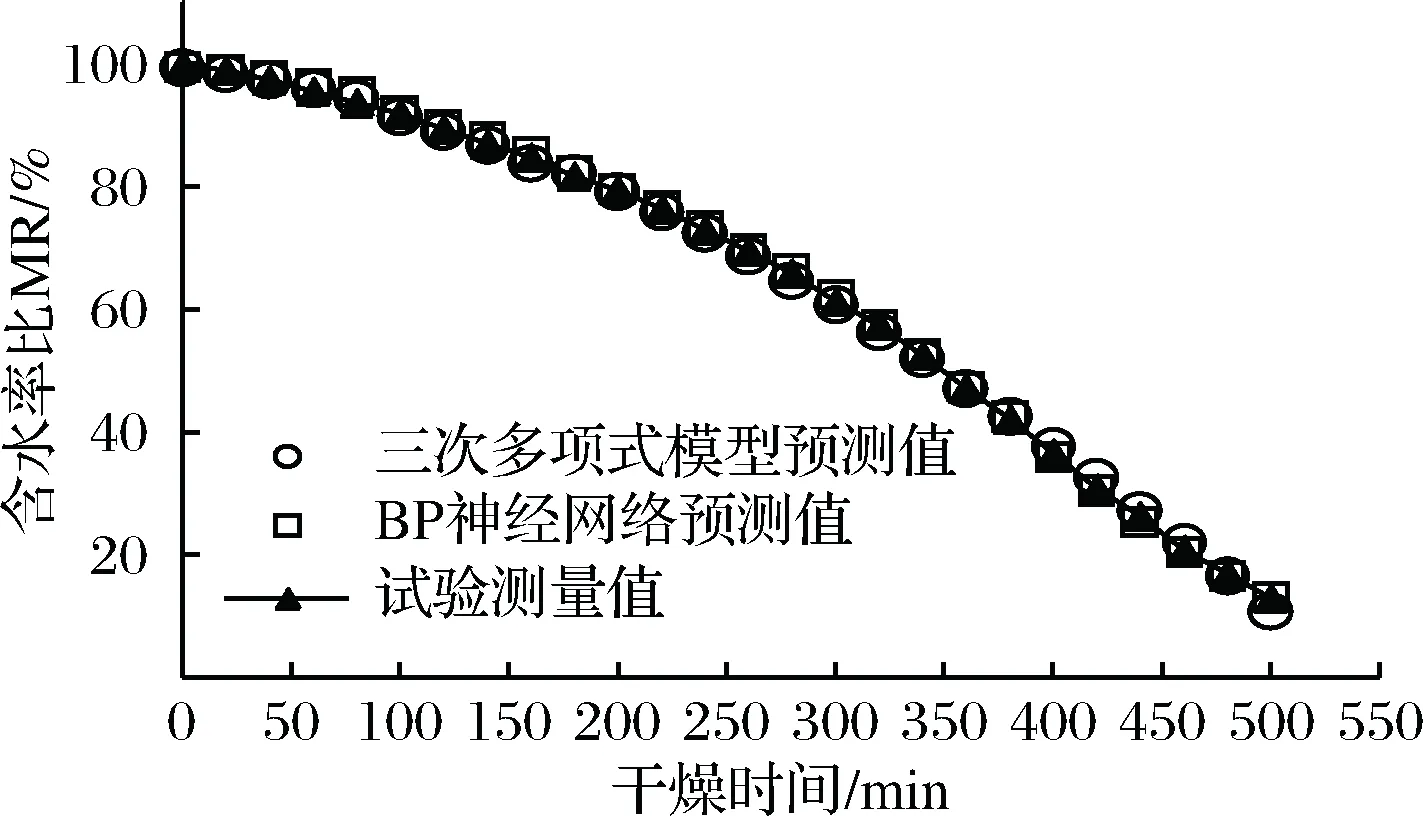
Fig.7 Curves of testing results for Cubic Polynomial Model and BP neural network3 结论

