陶瓷涂层-金属基-陶瓷涂层的金属基体超声波无损检测研究
陈正林 ,张雪飞 ,王高潮 ,王兴国
(1.南昌职业学院 工程系,江西 南昌 330500;2.景德镇陶瓷大学 机械电子工程学院,江西 景德镇 333403)
0 引 言
目前,金属是应用广泛的工程材料之一,但易腐蚀、易磨损的的缺点使得一些金属应用受到大大的限制,而陶瓷涂层覆金属基材料使其兼有金属的强韧性、可加工性及陶瓷的绝缘性、耐高温、耐磨损及耐腐蚀等优异性能[1-2]。也正因如此,国内外许多学者研究了陶瓷涂层-金属基-陶瓷涂层三明治结构。比如,李艳征[3]等人用解析法研究了在第3类边界条件下双面陶瓷涂层三明治板的瞬态温度场及瞬态热应力场。Pantelis D I和Lackey W J[4-5]等人研究了铁基底上Al2O3陶瓷涂层是一种优质的复合材料,其工业应用前景广阔;隋育松[6]等人用陶瓷、金属基/金属间化合物基复合材料(MMC/IMC)、陶瓷基复合材料(CMC)等耐热温度更高的新材料替代现在的耐热高温合金航空发动机涡轮叶片,取得较好的效果;赵军[7-9]等人研究了Al2O3基梯度纳米复合陶瓷刀具材料的抗热震性和强韧化机理”在航空、航天、石化等工程领域中常在钛合金管道表面制备氧化铝涂层[10-12]。尽管近年来利用激光协同原位合成技术增强陶瓷涂层与金属基之间的结合强度[13-15]。但陶瓷涂层与金属表面由于物理和化学上的巨大差异,得不到理想的结合强度,使用过程中涂层的剥落难以避免[16],因此对陶瓷涂层-金属基-陶瓷涂层性能检测与评价就显得尤为重要。
尽管有多种方法用于陶瓷涂层-金属基-陶瓷涂层的金属基体性能检测与评价,但超声波检测技术是最为有效直接的方法之一[17]。目前国内外已广泛运用超声技术检测三层三明治层状介质的物理特性,比如刘彬研究了激光熔覆层厚度对超声表面波评价表层缺陷深度的影响[18],程西云等人研究了梯度结构对氧化铝陶瓷涂层结合强度及抗冲击性能影响的试验研究[19]。张锐等人研究了超薄覆层低频超声类瑞利波定征方法[20],但对金属基体在生产及在役使用过程中的性能检测研究较少,尤其是在高温、寒冷等恶劣环境下。本文结合声波控制方程并采用势函数和传递法,建立了陶瓷涂层-金属基-陶瓷涂层之间的超声波检测全局矩阵数学模型,得到了声波在固体层状介质中的声传播频散曲线。研究了陶瓷涂层-金属基-陶瓷涂层的金属基体物理参数变化对声波频散曲线影响。为陶瓷涂层-金属基-陶瓷涂层的金属基体性能无损检测及结构健康监测提供理论依据。
1 声波在三层介质中的传播特性
1.1 物理模型
图1是声波入射三层夹心层状介质传播示意图。第一层为陶瓷涂层,第二层为金属基体,第三层为陶瓷涂层。需要说明的是第一层和第三层为同一种陶瓷涂层材料。一束频率为ω的纵波(简称“L波”),横波(简称“SV波”)以入射角θ入射到界面i1处并反射L波,SV波和透射L波,SV波,透射波接着在下一界面处发生反射和透射现象,最后在界面i4处透射到空气中。涂层厚度为h1,密度ρ1,拉梅常数λ1,μ1;基体厚度为h2,密度ρ2,拉梅常数λ2,μ2。
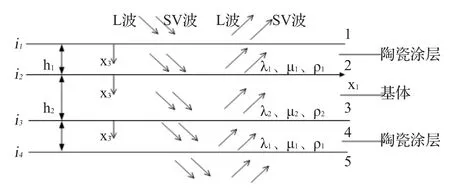
图1 声波入射三层层状介质传播示意图Fig.1 The schematic diagram of sound wave propagation through the three-layered medium
以u1、u3分别表示该固体层中的声场的质点水平位移、质点垂直位移[21]
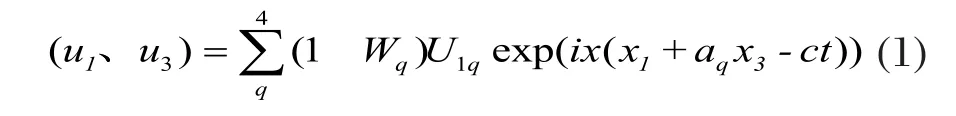
其中,W1q=U3q/U1q(q=1,2,3,4), U1q为u1的振幅,U3q为u3的振幅,α为方程(2)的解:
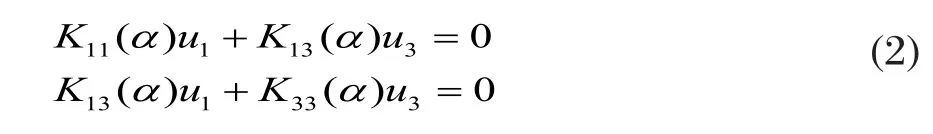
由于u=(u1, u3)不为零的条件是方程式(2)系数行列式等于零,即:

对式(3)进行展开求解可得以α为变数的六阶多项式方程:

其中,A=(λ + 2μ)μ,B=(λ + 2μ - ρc2) (λ + 2μ) + (μρc2)μ- (λ + 2μ)2,C=(λ + 2μ - ρc2) (μ - ρc2) ,λ和μ材料拉梅常数,ρ为介质密度,c为声波在介质中的声速。根据式(1)-(4)可得第n层位移和应力的形式解Pn=DnUn,且
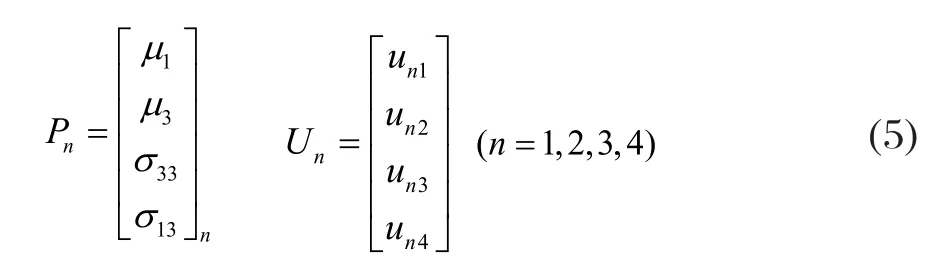
un1、un3分别表示第层中的下行纵波、下行横波在x1上的投影,un2、un4分别表示上行纵波、上行横波在x1上的投影。根据声波在层状介质中的传播特性可以得到声波在介质中的位移应力的关系表达式,如

其中:

其中,cL、cT分别为介质中的纵波声速和横波声速。
以Dt表示上表面的传递矩阵,Db表示下表面的传递矩阵,则
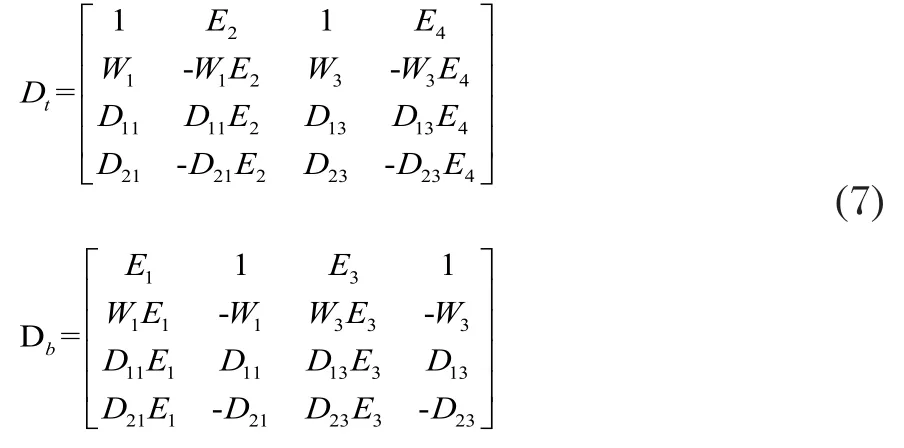
1.2 声波在三层层状介质中的传播边界条件
对每一个界面处,位移和应力的连续性,如式(8)所示:

根据边界条件式(8)可以得到声波在三层层状介质中传播特性的矩阵方程Ax=0,如式(9)所示:
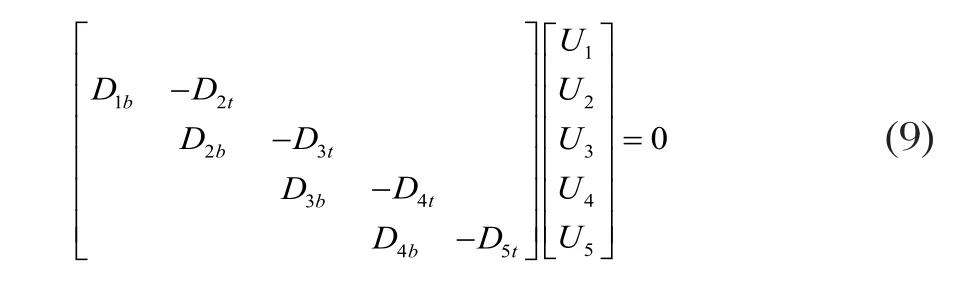
在第1层半无限空间里下行波和第4层半无限空间里,“进入”薄层和基体的波均为0,用“+”、“-”分别表示下行波和上行波,因此:
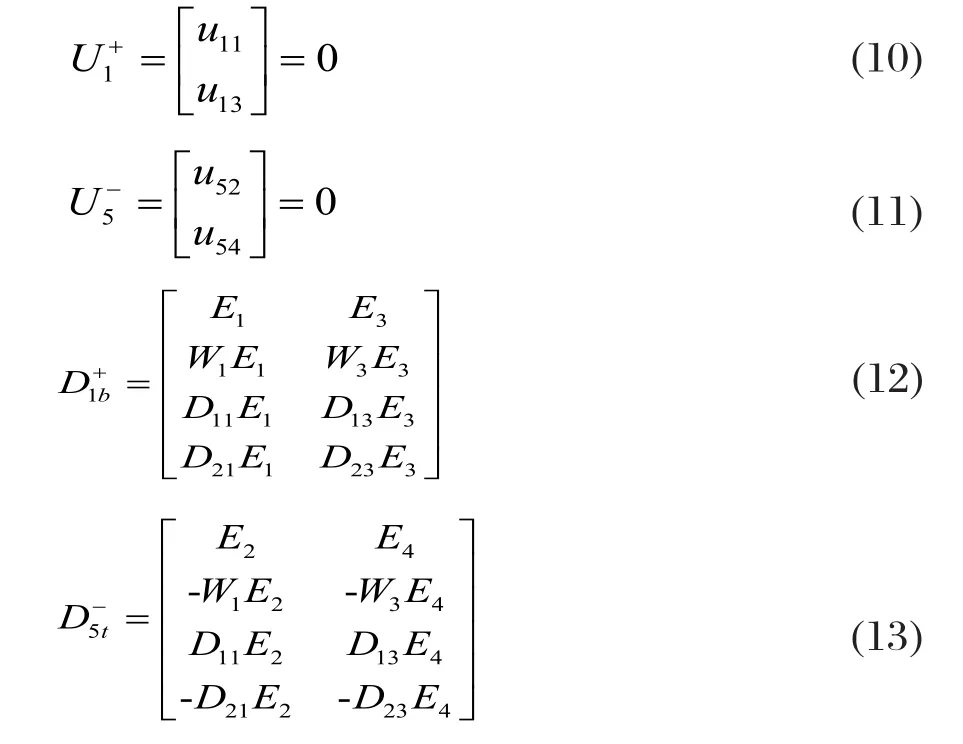
根据式(10)、式(11)、式(12)、式(13)带入边界条件式(9)中可以得到Ax=0 形式的声波在三层层状介质中的传播频散特性方程式(14)。
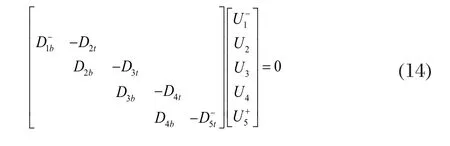
2 声波在三层层状介质中的传播频散特性数值仿真
以氮化硅陶瓷为涂层,钢和铝分别作为金属基体,通过求解公式(14)可以获得声波在陶瓷涂层-金属基-陶瓷涂层层状介质中的频散曲线,表1给出了氮化硅陶瓷、钢和铝的声学参数[22-23]。
2.1 金属基体密度对频散特性的影响
图2为陶瓷涂层-金属基-陶瓷涂层结构中金属基体不同密度对声波频散曲线的影响。金属基体厚度均为3 mm,氮化硅陶瓷涂层厚度为1 mm,其中空心曲线是金属基体为铝材质时的声波频散曲线,实心曲线是金属基体为钢材质的声波频散曲线。从图中可以看出,金属基体为铝材质的频散曲线整体上往右移动,且当声波频率小于1 MHz时,S0模态对陶瓷涂层-金属基-陶瓷涂层三明治结构的金属基体密度变化非常敏感。由此可见可以选择合适的频率激发S0模态进行检测或监测陶瓷涂层-金属基-陶瓷涂层层状介质金属基体的密度变化,以免在役设备或结构因金属基体密度退化而失效。

表1 氮化硅、钢和铝的声学参数表Tab.1 The acoustic parameters of silicon nitride, steel and aluminum
2.2 金属基体厚度对频散特性的影响
图3为陶瓷涂层-金属基-陶瓷涂层介质中金属基体不同厚度对频散曲线的影响。其中以钢材质作为金属基体,氮化硅陶瓷薄层厚度为1 mm。空心曲线是金属钢基体厚度为1 mm的频散曲线,实心曲线是金属基体厚度为3 mm的频散曲线。从图中可以看出,当金属基体的厚度从1 mm增加到3 mm时,声波在介质中的频散曲线整体上往左移动,且当声波频率小于1 MHz时,A0模态和S0模态声波对陶瓷涂层-金属基-陶瓷涂层三明治结构的金属基体厚度的变化较为敏感;由于S0模态的声波能量比A0模态高,声波指向性也较好,因此可以根据此频散曲线关系选择合适的频率激发S0模态检测和监测陶瓷涂层-金属基-陶瓷涂层三明治结构金属基体厚度的变化,以免在高温、寒冷等恶劣环境下在役设备或结构因金属基体厚度变化带来的隐患。
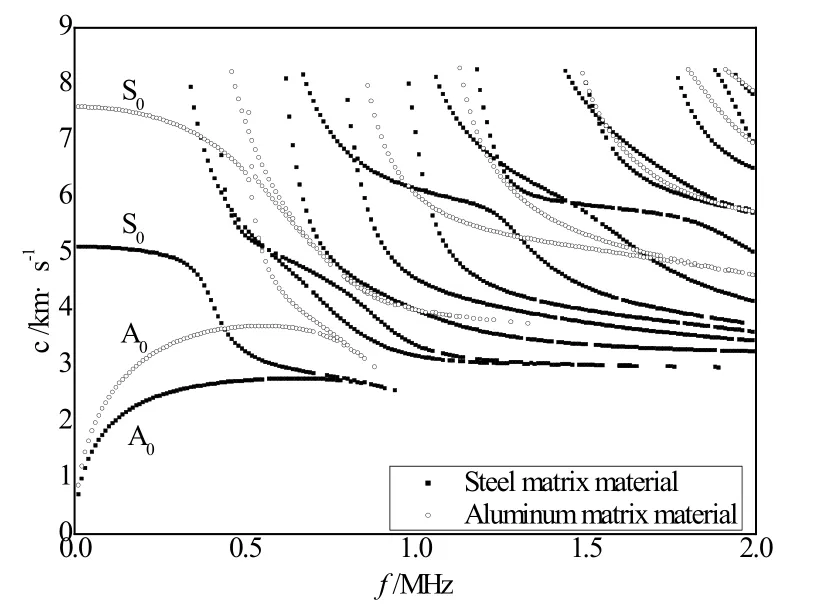
图2 三层介质中不同金属基体密度声波相速度频散曲线Fig.2 The ultrasonic phase velocity dispersion curves for the metal matrices of different densities in the three-layered media

图3 金属基体不同厚度的声波相速度频散曲线Fig.3 The ultrasonic phase velocity dispersion curves for the metal matrices of different thicknesses
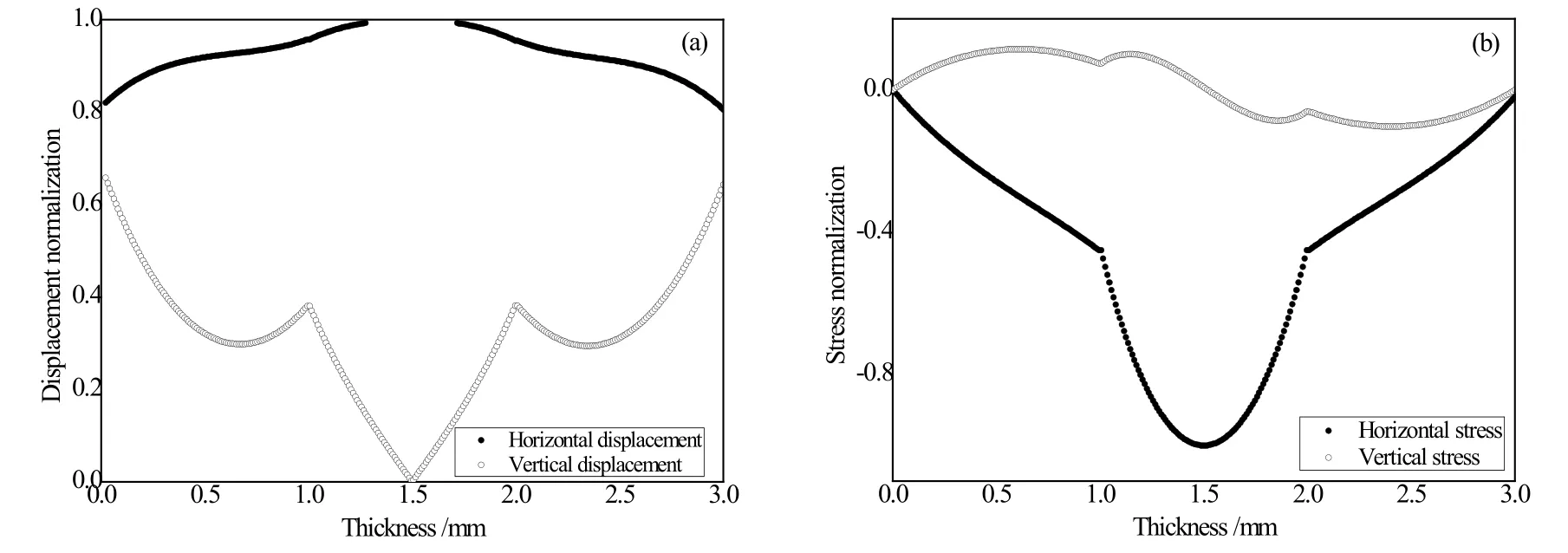
图4 质点位移在厚度方向上的分布Fig.4 The distribution of particle displacement and stress along the thickness direction: (a) particle displacement; (b) particle stress
2.3 斜入射时声波在陶瓷涂层-金属基-陶瓷涂层厚度方向上的位移和应力分布
通过上述对陶瓷涂层-金属基-陶瓷涂层结构的金属基体不同物理性能参量对相速度频散曲线的影响分析与研究,可进一步依据声波相速度的测定计算出陶瓷涂层-金属基-陶瓷涂层结构厚度方向上的位移和应力来分析金属基体物理性能。通过求解式(14)可得到声波在陶瓷涂层-金属基-陶瓷涂层结构中位移和应力在厚度方向上的传播规律。由上述部分分析可知,S0模态声波较适用于检测或监测陶瓷涂层-金属基-陶瓷涂层结构金属基体性能的变化。因此采用0.5 MHz S0模态声波在氮化硅陶瓷涂层及钢基体厚度分别为1 mm时厚度方向上的质点垂直和水平位移、应力的分布,如图4(a)和4(b)所示。图4(a)中空心曲线为声波垂直位移在介质厚度方向上的分布,实心曲线为声波水平位移在介质厚度方向上的分布。由图可知,声波水平位移和垂直位移在陶瓷涂层-金属基-陶瓷涂层结构厚度方向上呈现对称形式,当厚度小于一半厚度时,水平位移呈现递增趋势而垂直位移基本上呈现递减趋势;当厚度大于一半厚度时,水平位移基本上呈现递减趋势而垂直位移基本上呈现递增趋势。图4(b)为声波在陶瓷涂层-金属基-陶瓷涂层结构厚度方向上的应力分布。空心曲线为声波在垂直方向上的应力分布,实心曲线为声波在水平方向上的应力分布。由图可知,结构中的水平应力在厚度方向上呈对称形式,而垂直应力在厚度方向上呈反对称形式。当厚度小于一半厚度时,水平应力整体上呈现递减趋势而垂直应力基本上逐步递增;当厚度大于一半厚度时,水平应力整体上呈现递增趋势而垂直应力基本上呈现递减趋势。在实际陶瓷涂层-金属基-陶瓷涂层超声检测当中厚度方向上位移和应力是不可直接测量的,但却通过对陶瓷涂层-金属基-陶瓷涂层的声波相速度的测定计算出某一厚度上的位移和应力,进而与图4(a)和图4(b)的位移和应力分布曲线相对比,可判断陶瓷涂层-金属基-陶瓷涂层结构金属基体物理性能是否发生变化。
3 结 论
本文研究超声波在陶瓷涂层-金属基-陶瓷涂层层状结构中金属基体物理性能的检测应用。采用全局矩阵传递法和声波控制方程结合界面处应力和位移连续性的边界条件得到了声波在陶瓷涂层-金属基-陶瓷涂层中的数学模型,获得了金属基体不同物理参量的声传播频散曲线,研究了陶瓷涂层-金属基-陶瓷涂层结构金属基体不同物理参数对声波频散特性的影响,得到如下规律:
(1)金属基体密度减小时的频散曲线整体上往右移动,在频率为1 MHz内A0模态变化较为敏感,而S0模态在整个频域内都较为敏感。由此可见金属基体材料密度的变化对声波的频散特性变化是明显的,尤其是S0模态对基体密度变化更为敏感,因此对于陶瓷涂层-金属基-陶瓷涂层层状介质基体的密度变化可以采用S0模态进行检测。当金属基体的厚度减小时,其频散曲线整体上往右移动,当声波频率小于1 MHz时,A0模态和S0模态对金属基体的厚度变化较为敏感;考虑到S0模态的能量较高且声波指向性较好,因此可以选择适当的频率激发S0模态检测和监测陶瓷涂层-金属基-陶瓷涂层三明治结构金属基体厚度的变化。
(2)S0模态声波在陶瓷涂层-金属基-陶瓷涂层三明治结构介质中的位移和应力在厚度方向上呈现一定的规律。当厚度小于一半厚度时,声波水平位移和应力呈现递减趋势,垂直位移基本上逐步递减而垂直应力基本上逐步递增;当厚度大于一半厚度时,声波水平位移和应力呈现递增趋势,垂直位移呈现递增趋势而垂直应力基本上呈现递减趋势。为超声检测陶瓷涂层-金属基-陶瓷涂层的金属基体物理性能参量变化提供一定的依据。
参考文献:
[1]王兴国, 陈正林, 吴文林, 等.陶瓷涂层-金属基体物理参量对声波传播特性的影响研究[J].中国陶瓷, 2016, 52(12): 41-45.WANG X G, CHEN Z L, WU W L, et al.China Ceramics,2016, 52(12): 41-45.
[2]李世普.特种陶瓷工艺学 [M].武汉: 武汉工业大学出版社,1990: 126-130.
[3]李艳征, 赵军, 艾兴.陶瓷涂层三明治板的抗热震性[J].硅酸盐学报, 2008, 36(8): 1168-1171.LI Y Z, ZHAO J, AI X.Journal of the Chinese Ceramic Society,2008, 36(8): 1168-1171.
[4]PANTELIS D I, PSYLLAKI P, ALEXOPOULOS N.Tribological behaviour of plasma-sprayed Al2O3coatings under severe wear conditions [J].Wear, 2000, 237(2): 197-204.
[5]LACKEY W J, STINTON D P, CERNY G A, et al.Ceramic coatings for advanced heat engines - A review and projection [J].Advanced Ceramic Materials, 1987, 2(1): 24-30.
[6]隋育松, 徐可君, 江龙平, 等.陶瓷涂层在航空发动机涡轮叶片表面处理中的应用[J].材料保护, 2001, (3): 38-40.SUI Y S, XU K J, JIANG L P, et al.Materials Protection, 2001, (3):38-40.
[7]李艳征.Al2O3基梯度纳米复合陶瓷刀具的研制及切削性能研究[D].济南:山东大学博士学位论文, 2011.
[8]YING A, ABDOU M, WONG C, et al.An overview of US ITER test blanket module program [J].Fusion Engineering and Design,2006, 81: 433-441.
[9]郭智慧, 黄群英, 宋勇, 等.CLAM钢基体上大气等离子体喷涂制备氧化铝涂层工艺研究[J].核科学与工程, 2008, (4): 295-299.GUO Z H, HUANG Q Y, SONG Y, et al.Chinese Journal of Nuclear Science and Engineering, 2008, (4): 295-299.
[10]SALAVY J F, BOCCACCINI L V, LÄSSER R, et al.Overview of the last progresses for the European test blanket modules projects [J].Fusion Engineering and Design, 2007, 82: 2105-2112.
[11]BENYAHIA F, ALBEDAH A, BOUIADJRA B B.Analysis of the adhesive damage for different patch shapes in bonded composite repair of aircraft structures [J].Materials & Design, 2014, 54: 18-24.
[12]成亚君.涂料喷涂的常见漆膜缺陷及成因[J].上海涂料, 2012,50(10): 42-45.CHENG Y J.Shanghai Coatings, 2012, 50(10): 42-45.
[13]GOPAGONIA S, HWANGA J Y, SINGHA A R P, et al.Microstructural evolution in laser deposited nickel-titaniumcarbon in situ metal matrix composite [J].Journal of Alloys and Compounds, 2011, (509): 1255-1260.
[14]陈正林, 肖任贤, 王兴国等.氮化硅陶瓷的空气耦合超声纵波传播特性研究[J].陶瓷学报, 2015, (4): 405-409.CHEN Z L, XIAO R X, WANG X G, et al.Journal of Ceramics,2015, (4): 405-409.
[15]孙海勤, 晁明举, 敬晓定, 等.原位生成 VC 颗粒增强镍基激光熔覆层研究[J].激光杂志, 2008, (5): 69-71.SUN H Q, CHAO M J, JING X D, et al.Laser Journal, 2008, (5):69-71.
[16]孙国梁, 王刚, 张文杰.金属基陶瓷涂层的制备及涂覆工艺的研究[J].陶瓷学报, 2013, (3): 318-321.SUN G L, WANG G, ZHANG W J.Journal of Ceramics, 2013, (3):318-321.
[17]王兴国, 吴文林, 陈正林, 等.空气耦合超声斜入射均匀弹性层状介质材料的传播特性[J].兵工学报, 2016, (11): 2094-2100.WANG X G, WU W L, CHEN Z L, et al.Acta Armamentarii,2016, (11): 2094-2100.
[18]刘彬, 董世运.激光熔覆层厚度对超声表面波评价表层缺陷深度的影响[J].无损检测, 2015, (1): 7-10.LIU B, DONG S Y.Nondestructive Testing, 2015, (1): 7-10.
[19]程西云, 肖舒, 何俊.梯度结构对氧化铝陶瓷涂层结合强度及抗冲击性能影响的试验研究[J].机械工程学报, 2014, (10): 87-92.CHENG X Y, XIAO S H J.Journal of Mechanical Engineering,2014, (10): 87-92.
[20]张锐, 万明习, 李刚, 等.超薄覆层低频超声类瑞利波定征方法[J].材料科学与工程学报, 2000, (1): 19-24.ZHANG R, WAN M X, LI G, et al.Materials Science and Engineering, 2000, (1): 19-24.
[21]张海燕, 刘镇清, 吕东辉.全局矩阵法及其在层状各向异性复合板中Lamb波传播特性研究中的应用[J].复合材料学报,2004, (2): 111-116.ZHANG H Y, LIU Z Q, LU D H.Acta Materiae Compositae Sinica, 2004, (2): 111-116.
[22]吴南星, 陈正林, 廖达海.基于lamb波在氮化硅陶瓷叶片及其作摩擦材料镀层传播特性的研究[J].陶瓷学报, 2015, (1): 1-3.WU N X, CHEN Z L, LIAO D H.Journal of Ceramics, 2015, (1):1-3.
[23]单英春, 徐久军, 李江涛, 等.制备工艺对热压Y-α-SiAlON陶瓷微结构及光学性能的影响[J].稀有金属材料与工程, 2007,(4): 3-4.SHAN Y C, XU J J, LI J T, et al.Rare Metal Materials and Engineering, 2007, (4): 3-4.