隧道上台阶分区爆破振动规律

，

(山东科技大学 矿业与安全工程学院，山东 青岛 266590)

城市地铁隧道作为重要的交通枢纽，多修建在主城区干路。采用钻爆法开挖隧道产生的振动会对邻近建(构)筑物、管线产生不利影响。而随着隧道工程的发展，线路大幅增加，难免出现相互交叠的情况[1-5]。研究近距离交叉隧道爆破施工技术以及振动规律，对于保护既有隧道的安全稳定具有重要的意义。目前交叉隧道爆破振动规律主要是针对全断面法爆破提出的。如赵东平等[6]建立数值模型得出新建隧道在距离交叉点 10 m 以外位置以全断面法爆破施工时，既有公路隧道二次衬砌的响应规律，确保施工安全。赵春生[7]根据现场监测数据分析新建隧道上跨既有隧道爆破振动规律，得出振速随起爆交叉点距离变化规律。李连超[8]利用Midas/GTS有限元分析软件分析童家院子出入线隧道施工断面距交叉段 0、25、50 m 不同距离下隧道衬砌振速规律，发现一次起爆药量与合位移、合速度、合加速度的大小成正比。而分区爆破振动规律主要参考浅埋隧道爆破引起的地表质点振动规律。如张继春等[9]在渝怀铁路人和场浅埋隧道进行现场试验，爆破试验各段延期时间均不小于200 ms，以保证相邻段别产生的振动波不会相互影响，得出掏槽孔振动强度是其他各类炮孔的2倍以上。孟海利[10]采用毫秒延时起爆网路将隧道断面分为掏槽区、辅助区、周边区依次起爆，利用延期时间间隔在时间域上得出不同爆破区域的振动衰减参数，并非严格意义上空间域上的爆破分区，而且并未对振动速度分布规律进行研究。

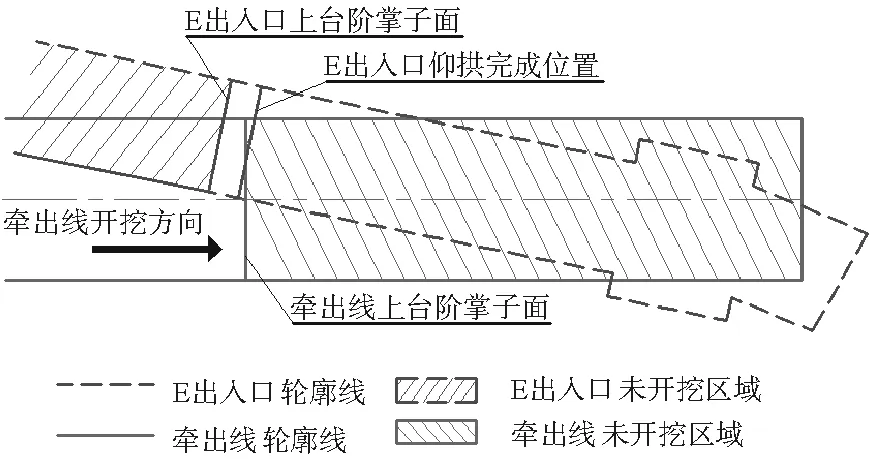
图1 牵出线与E出入口平面位置关系图Fig.1 Planimetric position relations of shunting-tunnel and E entrance

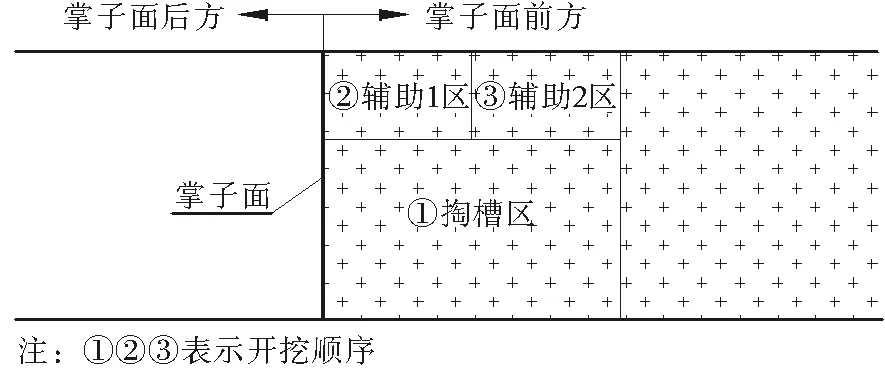
图2 各分区剖面位置关系

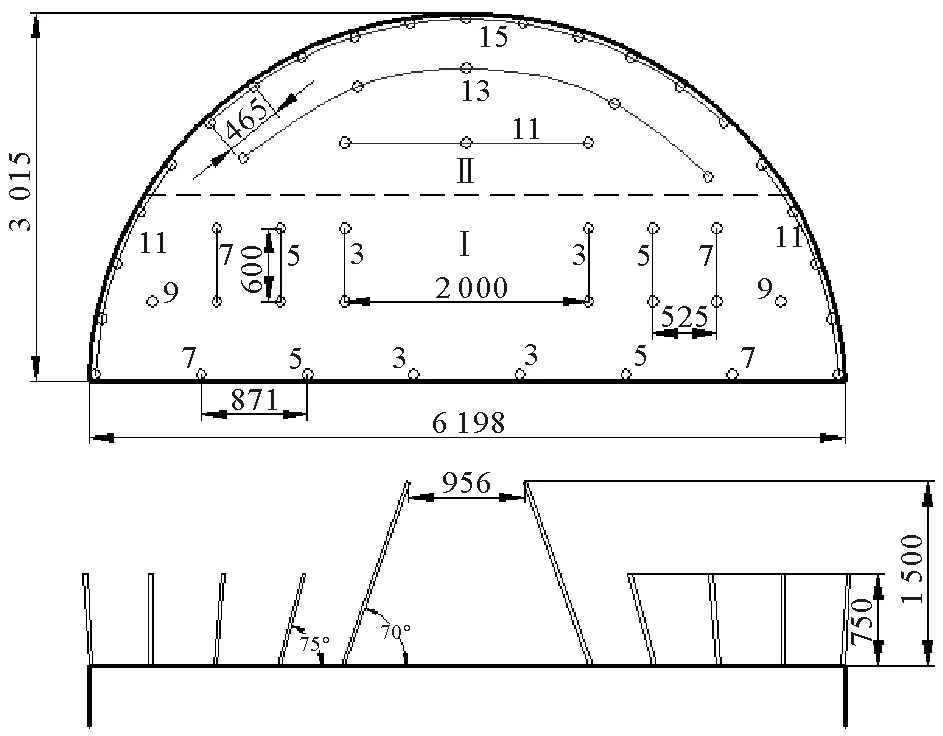
图3 上台阶炮孔布置图

本研究通过现场试验，在空间域上对上台阶进行分区，并对分区爆破振动特性进行系统研究。完善了分区爆破振动规律，同时对类似工程提供参考，以期保证既有隧道的安全稳定。

1 试验设计

1.1 试验背景

辽阳东路车辆基地牵出线为单线隧道，其拱顶正上方垂直距离3 m处为汽车东站E出入口，两隧道平面夹角12°，平面位置关系见图1。

试验研究是以《爆破安全规程GB 6722—2014》[11]中的交通隧道爆破振动安全允许标准为控制爆破振动大小的依据。牵出线施工段属Ⅴ级风化花岗岩，围岩破碎。同时，为避免爆破振动对E出入口的影响，对爆破方案进行优化。施工方法由全断面开挖法调整为上下台阶法，上台阶宽6.198 m，高3.015 m，缩短循环进尺至0.75 m，并且上台阶分三区(定义为：掏槽区Ⅰ、辅助区Ⅱ；辅助区又包括：辅助1区、辅助2区)三次爆破。其施工工序为：爆破掏槽区Ⅰ，进尺1.5 m→爆破辅助1区，进尺0.75 m→出渣→立拱架→喷浆→爆破辅助2区，进尺0.75 m→下一循环。各分区剖面位置关系如图2。上台阶炮孔布置如图3，爆破参数如表1。

1.2 测点布置及监测

使用成都中科测控生产的TC-4850爆破测振仪进行监测。该仪器为三通道并行采集，采样频率1～50 kHz，频响范围0～>10 kHz，自适应量程，最大输入值35 cm/s。

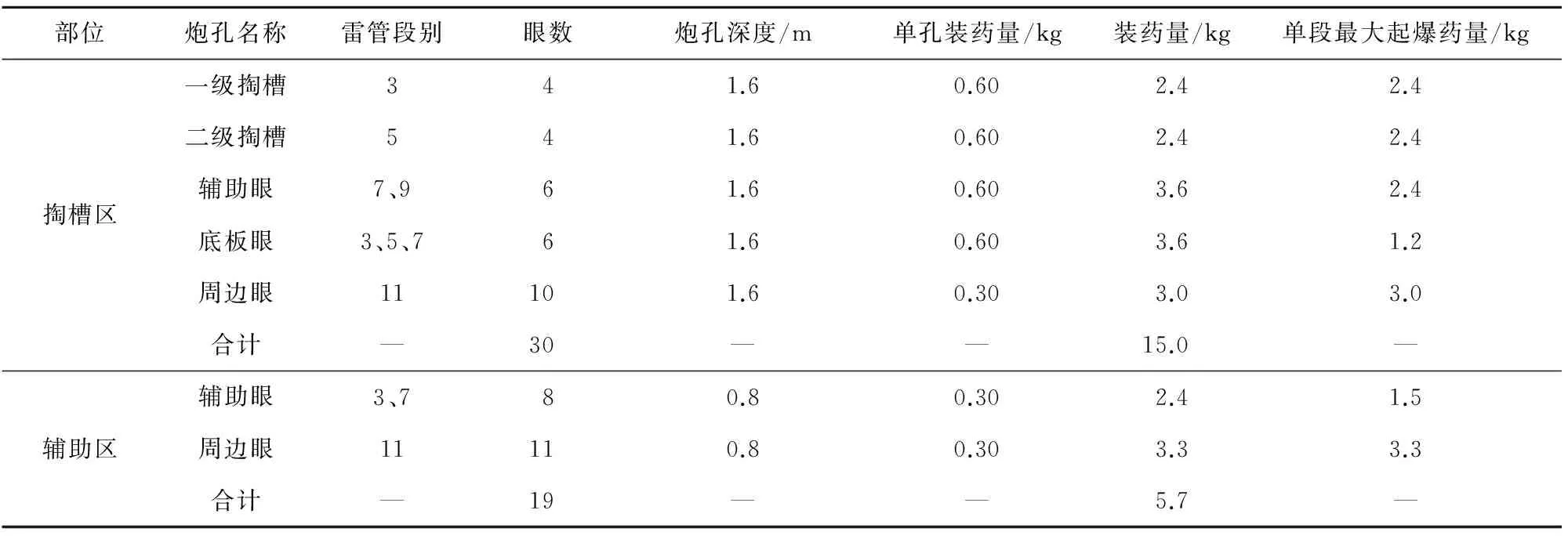
表1 上台阶爆破参数表

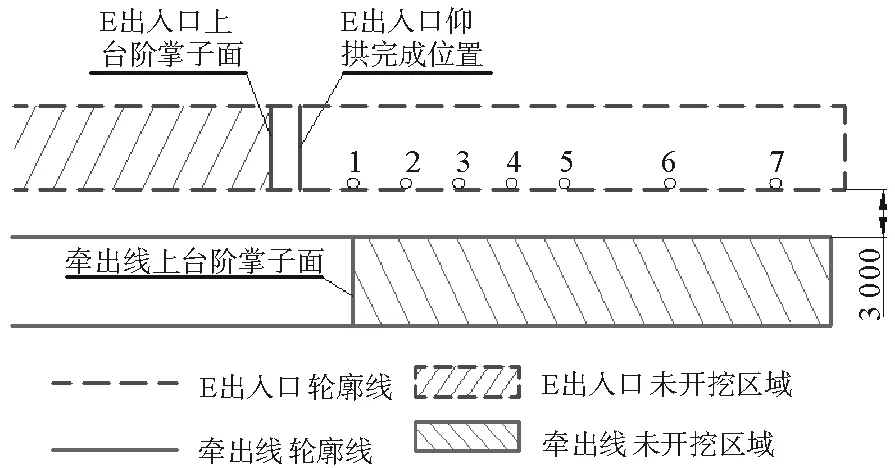
图4 方案A测点剖面布置图

本试验使用仪器7台，设置采样频率8 kHz，采样时间2 s。提出3种监测方案：A、在掌子面前方共布置7个测点，因现场施工条件限制，测点间距依次为1 m、1 m、1 m、1 m、2 m、2 m；B、在掌子面后方共布置7个测点，测点间距依次为1 m、2 m、3 m、3 m、4 m、4 m；C、以掌子面为基准点前后各布置3个测点，间距1 m。在此给出方案A测点布置如图4，方案B、C布置方式类似。试验共监测17组数据，其中2组数据因操作、现场施工误碰问题，导致数据记录不完全。对所监测数据整理，提取X、Y、Z三个方向最大振速作为研究对象。方案A测点1监测信号波形图如图5，部分监测数据如表2所示。

图5 测点1波形图

2 振动速度变化规律

通过现场监测数据，绘制振速-距离曲线(如图6～8)。曲线总体呈现出震荡变化特征，具体如下：

1) 由图6得出，辅助1区爆破掌子面前方2～3 m处出现极大值，而辅助2区爆破掌子面前方振速变化不明显，这是由于辅助1区爆破时，前方存在一段空顶距，应力波在此区域发生反射、折射导致振速放大。掏槽区掌子面前方1 m处出现极大值，与辅助2区比较，装药量大，掏槽形式不同等因素导致。

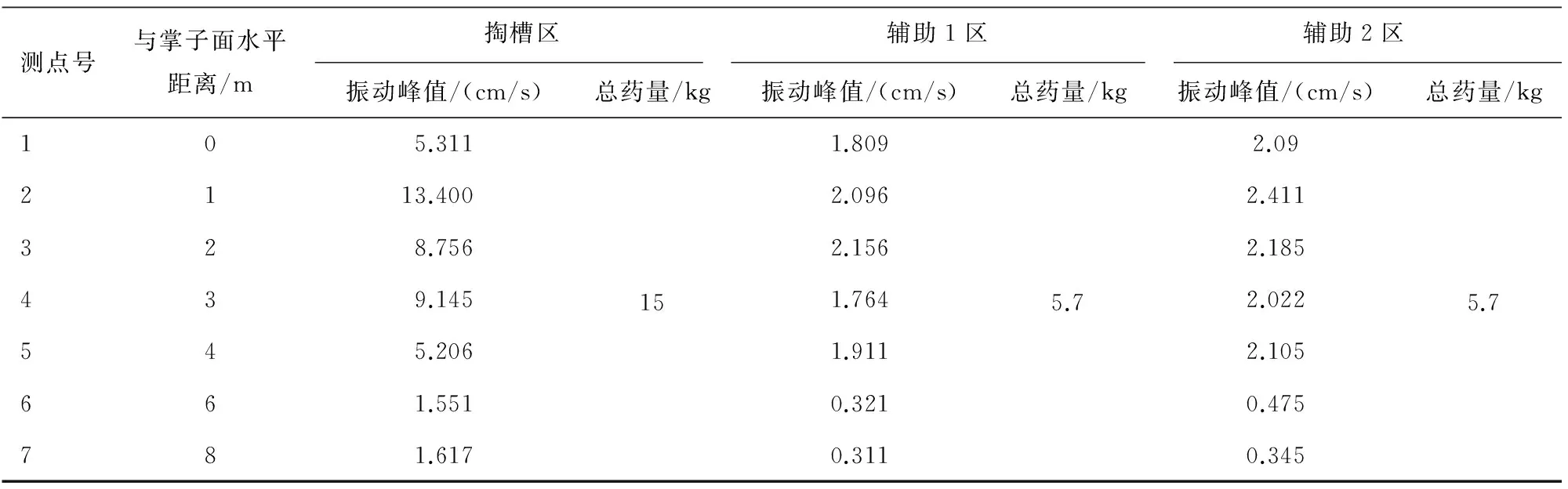
表2 方案A振动监测数据

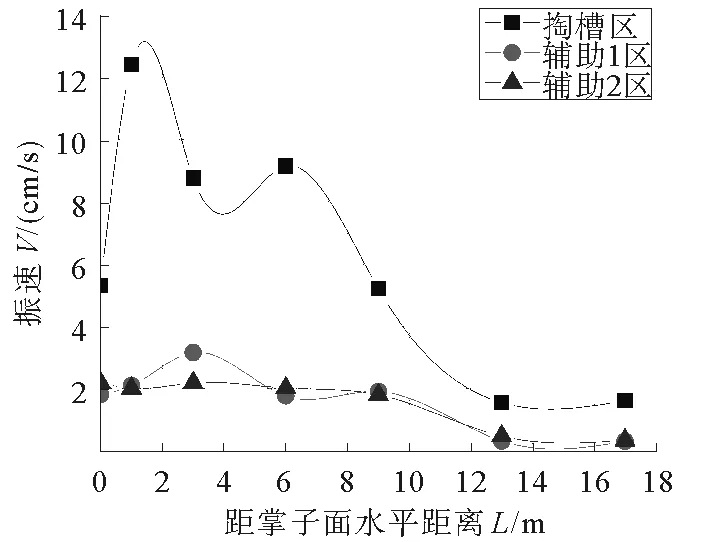
图6 掌子面前方振速规律图Fig.6 The law of the front vibration velocity of the palm face

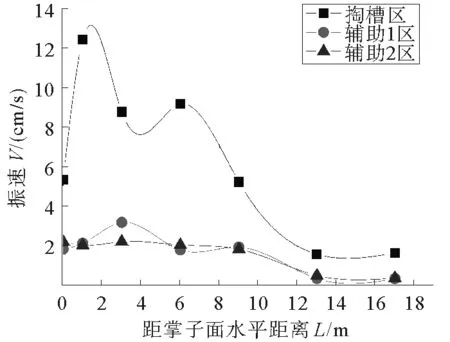
图7 掌子面后方振速规律

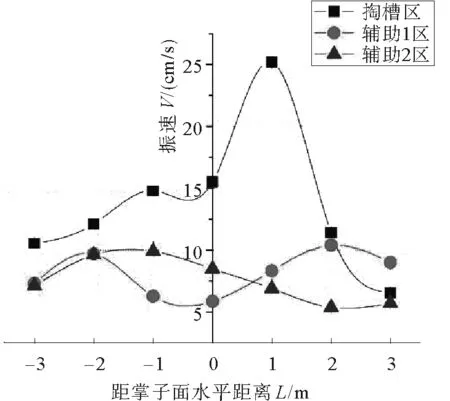
图8 掌子面前、后方3 m范围振速规律

2) 掌子面后方已开挖区岩层性质发生改变，形成空洞。由图7可知，在辅助区爆破时，药量相对较小(5.7 kg)，2个自由面，空洞放大作用抑制振速减小，反而在1～3 m处出现极大值[12-13]。而在掏槽区爆破时，装药量相对较大(15 kg)，1个自由面，空洞放大效应不明显，振速先减小后增大，6～9 m处出现极大值。

3) 由图8得出基准点前后3 m范围内，掏槽区、辅助2区掌子面后方振速普遍大于前方，A-1点除外，这种现象定义为“空洞效应”[14-16]，掏槽区放大系数1.1～1.6，辅助2区放大系数1.2～1.8。而辅助1区由于空顶距区域应力波反射、折射放大作用大于空洞放大作用，导致掌子面前方振速大于后方振速。

3 振动波衰减规律

不同分区、掌子面前后方爆破地震波衰减规律不同。为此，分别计算相应的衰减参数。通常采用萨道夫斯基公式

(1)

式中：V为测点振动速度，cm/s；Q为最大单段装药量，kg；R为测点与爆源间的距离，m；K、α为与爆破点至计算保护对象间的地形、地质条件有关的系数和衰减指数。

根据监测数据回归分析绘制各分区衰减曲线，如图9所示。回归分析得出各分区爆破振动衰减方程如表3。K、α取值并非严格对照《爆破安全规程》13.2.4取值，而且相差较大，因此爆破施工中要进行实际监测分析，更科学的指导工程，保护建筑物的安全。

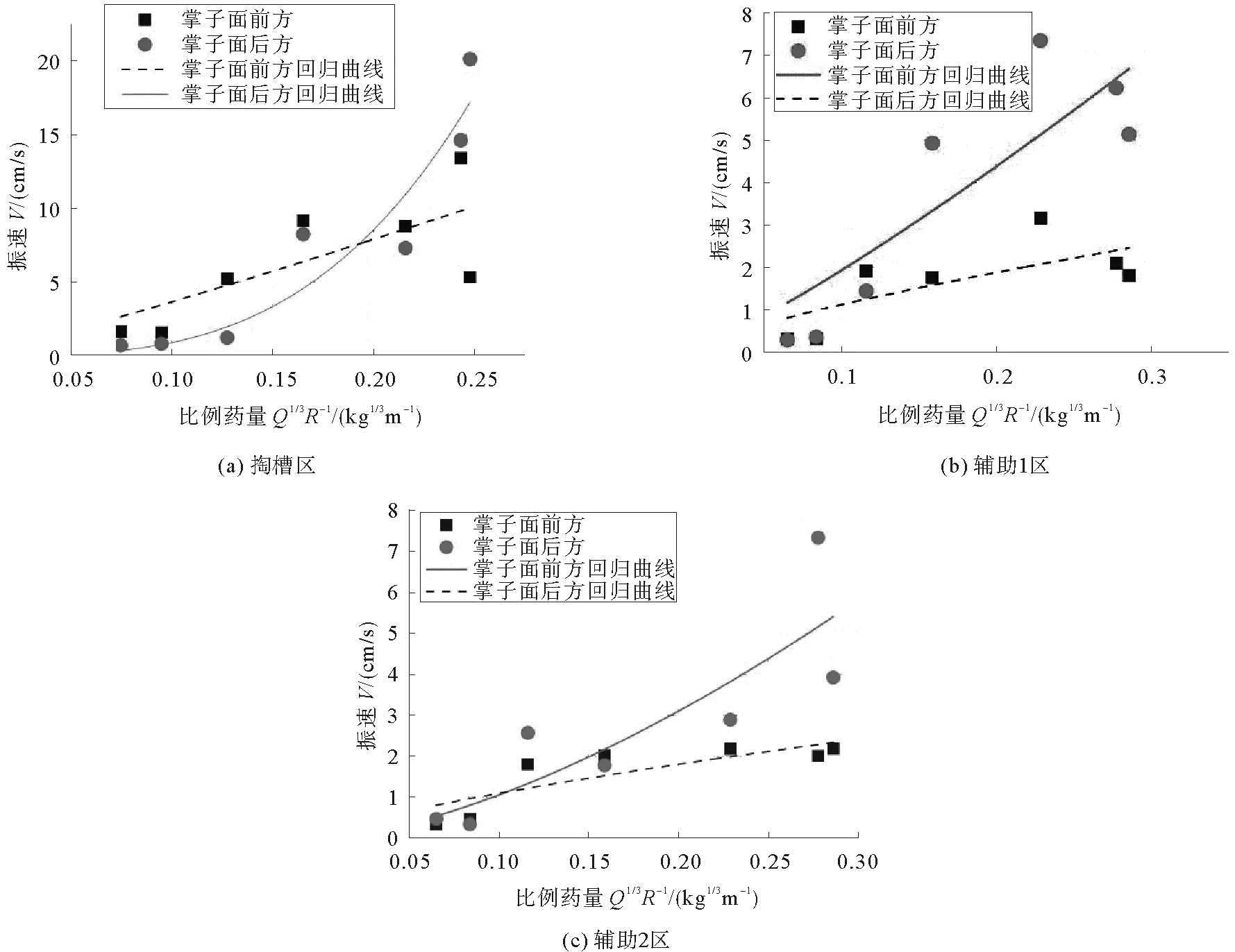
图9 爆破振动衰减曲线

爆破位置 掏槽区辅助1区辅助2区回归方程相关系数R2回归方程相关系数R2回归方程相关系数R2掌子面前方y=91.086x1.5490.7513y=15.761x1.3570.7124y=12.031x1.18670.7641掌子面后方y=883.77x2.90160.9170y=138.65x2.2270.8857y=45.603x1.71280.8150

由图8可知，无论是掏槽区爆破还是辅助区爆破，掌子面后方K、α值均大于前方(如掏槽区衰减参数：K值883.77>91.086，α值2.901 6>1.549)。这表明，后方开挖已形成的断面围岩性质发生改变，品质因子Q减小，爆破振动在此区域衰减加快。

在掌子面后方区域，掏槽区振动衰减速率>辅助1区>辅助2区；在掌子面前方区域，掏槽区振动衰减速率>辅助区。掏槽区装药量大，只有一个自由面，应力波在此区域衰减快。辅助1区与辅助2区爆破参数基本一致，振动衰减速率相差不大，表明辅助1区爆破时，空顶距对衰减参数影响不明显。

4 振动频率变化规律

辅助1区与辅助2区爆破振动频率变化规律基本一致，为便于与掏槽区爆破振动频率进行分析比较，以下研究统称为辅助区。

4.1 主振频率变化规律

主振频率是介质质点最大振幅所对应波的频率。由图10(a)得，掏槽区、辅助区爆破振动主振频率随爆心距的增加总体上呈现衰减趋势，但并非严格单调下降，在水平距0～9 m范围内总体呈现上升趋势，而在水平距9～17 m范围内呈现下降趋势，而且主振频均大于建筑物固有频率，不会发生共振现象。辅助区各测点主振频率普遍大于掏槽区对应测点主振频率。这是由于相比掏槽区爆破，辅助区炸药量小，2个自由面，爆破产生的应力波经自由面发生反射形成稀疏波，反射稀疏波与原应力波叠加致使爆炸荷载压力的上升时间和持续作用时间缩短，造成频率变大。

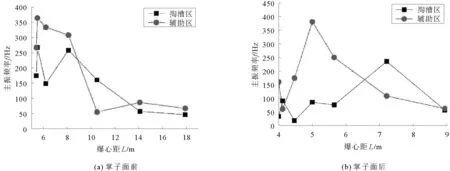
图10 掌子面前、后方爆破振动主振频率衰减曲线

由图10(b)可知，在水平距0～8 m范围内掏槽区主振频率总体变化不大，个别测点出现跃升；辅助区主振频率呈现先增大后减小的趋势。掏槽区主频频率较辅助区低，而且最低主频为18.018 Hz，接近建筑物固有频率。因此，工程中应在掌子面前方加强地表爆破振动监测，及时调整爆破参数，避免掏槽区爆破引起地面建筑物共振、造成破坏。

4.2 质心频率变化规律

由图10也可以看出，主振频率随距离变化曲线并无显著的规律性，出现局部突变现象，无法准确预测后期的变化，不能很好地反映振动的频谱构成及其衰减规律，因而采用质心频率也称为平均频率[17]，定义为

(2)

式中：fc为质心频率，Hz；Ai为频率fi对应的振动速度谱。

采用质心频率拟合曲线相关系数高分别为0.862 5和0.774 7。由图11可见，随着距离的增加，质心频率呈现先增大后减小的趋势。辅助区质心频率在水平距7 m处开始下降，衰减速率快，而掏槽区质心频率在水平距15 m处才开始下降。

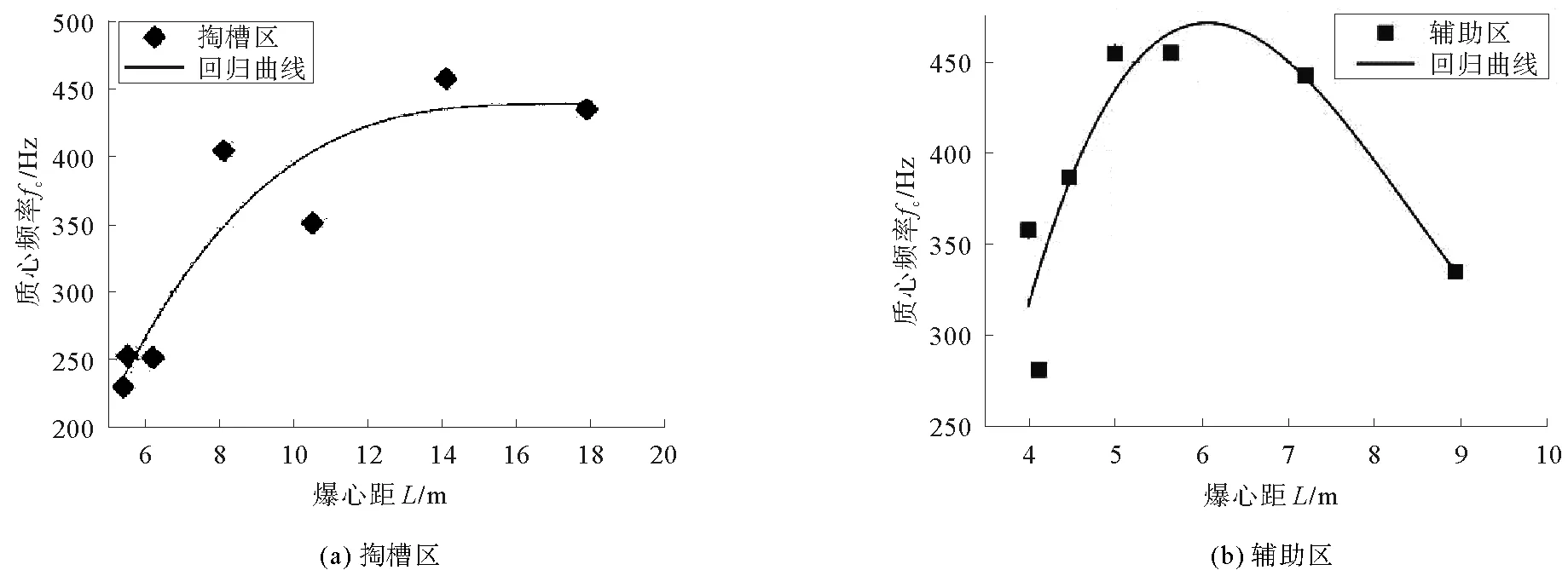
图11 掏槽区(a)与辅助区(b)爆破掌子面前方质心频率随爆心距变化拟合曲线

5 结论

以辽阳东路车辆基地牵出线与汽车东站E出入口两条立体交叉隧道，垂直距离仅3 m为工程背景，研究近距离隧道上台阶分区(掏槽区、辅助1区、辅助2区)爆破振动规律：

1) 各分区爆破振动速度呈震荡变化规律。装药量、空顶距等因素的影响导致掏槽区、辅助1区爆破时在掌子面前方1～3 m处出现极大值。掌子面后方存在空洞放大效应，且受装药量、自由面、空顶距等因素影响，掏槽区放大系数1.1～1.6，辅助2区放大系数1.2～1.8，而辅助1区掌子面前方振速大于后方振速。

2) 各分区爆破时对振动数据回归分析得出K、α值，掌子面后方K、α值均大于前方，掏槽区振动衰减速率>辅助区。

3) 主振频率随距离变化曲线并无显著的规律性，不能很好反映振动的频谱构成及其衰减规律，而采用质心频率得出较强的规律性，随着距离的增加质心频率呈现先增大后减小的趋势。

本研究只从振动速度、频率角度研究各分区爆破振动响应规律，后续研究可从振动信号频带能量分布方面进一步分析。

参考文献：

[1]GONG L,QIU W,WANG F.Closely constructing influence forecast of hydraulic tunnel under-cross existing railway tunnel[J].China Railway Science，2007,28(4):29-33.

[2]LO K W,CHANG L K,LEUNG C F,et al.Field instrumentation of a multiple tunnel interaction problem[J].International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts,1989,26(3/4):A227.

[3]ASANO T，ISHIHARA M，KIYOTA Y.An observational excavation control method for adjacent mountain tunnels[J].Tunneling and Underground Space Technology,2003,18(2/3):291-301.

[4]YAMAGUCHI I,YAMAZAKI I,KIRITANI Y.Study of ground-tunnel interactions of four shield tunnels driven in close proximity,in relation to design and construction of parallel shield tunnels[J].Tunneling and Underground Space Techno-logy,1998,13(3):289-304.

[5]JUNICA M I,AOKI K,IWAI K,et al.The assessment of influences on ground due to 2nd tunnel excavation based on 1st tunnel excavation[J].Tunneling and Underground Space Technology,2004,19(4):442.

[6]赵东平,王明年.小净距交叉隧道爆破振动响应研究[J].岩土工程学报,2007,29(1):116-119.

ZHAO Dongping,WANG Mingnian.Study on influence of blasting vibration on cross tunnels with small clearance[J].Chinese Journal of Geotechnical Engineering,2007,29(1):116-119.

[7]赵春生.新建隧道上跨既有隧道的爆破振动分析[J].工程爆破,2017,23(3):52-55.

ZHAO Chunsheng.New tunnel blasting vibration analysis on the existing tunnel[J].Engineering Blasting,2017,23(3):52-55.

[8]李连超.隧道爆破对既有下穿隧道的影响分析[D].重庆:重庆交通大学,2016.

[9]张继春,曹孝君,郑爽英,等.浅埋隧道掘进爆破的地表震动效应试验研究[J].岩石力学与工程学报,2005,24(22):4158-4163.

ZHANG Jichun,CAO Xiaojun,ZHENG Shuangying,et al.Experimental study on vibration effects of ground due to shallow tunnel blasting[J].Chinese Journal of Rock Mechanics and Engineering,2005,24(22):4158-4163.

[10]孟海利.隧道分区爆破振动传播规律试验研究[J].铁道建筑,2015(4):50-54.

MENG Haili.Experimental study on propagation law of tunnel blasting vibration[J].Railway Engineering,2015(4):50-54.

[11]中华人民共和国国家标准．GB 6722—2014,《爆破安全规程》[S].

[12]孙志果,王晓雯.浅埋隧道掏槽爆破地表质点震速规律研究[J].现代隧道技术,2015,52(1):163-167.

SUN Zhiguo,WANG Xiaowen.On the velocity law of ground particle vibration induced by cut blasting in a shallow-buried tunnel[J].Modern Tunnelling Technology,2015,52(1):163-167.

[13]向亮.城市浅埋硬岩大跨隧道开挖爆破振动监控研究[D].成都：西南交通大学,2009.

[14]喻军,刘松玉,童立元.浅埋隧道爆破振动空洞效应[J].东南大学学报(自然科学版),2010,40(1):176-179.

YU Jun,LIU Songyu,TONG Liyuan.Hollow effect induced by blasting vibration in shallow tunnels[J].Journal of Southeast University(Natural Science Edition),2010,40(1):176-179.

[15]杨云凌.浅埋隧道爆破振动空洞效应研究[J].爆破,2012,29(3):127-130.

YANG Yunling.Hollow effect induce by blasting vibration in shallow tunnels[J].Blasting,2012,29(3):127-130.

[16]高照帅,王德胜,尹作明,等.城市地铁浅埋隧道掘进爆破地表振动试验研究[J].山东科技大学学报(自然科学版),2016,35(1):79-85.

GAO Zhaoshuai,WANG Desheng,YIN Zuoming,et al.Experimental study of ground vibration induced by shallow urban subway tunnel excavation blasting[J].Journal of Shandong University of Science and Technology(Natural Science),2016,35(1):79-85.

[17]卢文波,张乐,周俊汝，等.爆破振动频率衰减机制和衰减规律的理论分析[J].爆破,2013,30(2):1-6.

LU Wenbo,ZHANG Le,ZHOU Junru，et al.Theoretical analysis on decay mechanism and law of blasting vibration frequency[J].Blasting,2013,30(2):1-6.