中立型时滞切换系统的有限时间有界性和增广耗散性分析
, ,
(聊城大学 数学科学学院,山东 聊城 252059)
切换系统是一类重要的混杂系统, 由有限数量的子系统及操纵这些子系统切换的逻辑规则组成,是混杂系统研究的重要方向,不仅有重要的理论价值,而且具有广泛的实际应用背景,如电力系统、机器人控制系统和车辆控制系统等。因此,切换系统得到国内外学者的广泛关注,出现了许多研究成果[1-5]。众所周知,时滞现象在许多工程系统中广泛存在,使得系统性能变差,甚至是导致系统不稳定的重要原因之一。中立系统是一类特殊的时滞系统,时滞现象不仅存在于状态而且存在于状态导数中。近年来,也涌现出很多关于中立系统稳定性[6-7]、H∞控制[8]等方面工作。
值得注意的是,目前大多数关于切换系统性能的文献集中于定义在无穷时间区间上的李雅普诺夫渐近稳定,而在有限时间内的系统动态性能的研究相对较少。文献[9],对一类切换系统引进了有限时间稳定的概念,文献[10]研究了切换系统有限时间有界与L2增益分析等。因此,对于时滞切换系统有限时间性能的进一步研究具有现实意义。同时,Zhang等[11]首次提出增广的耗散性概念,即通过矩阵参数调整,使增广的耗散性涵盖一些著名的性能指标如H∞、L2-L∞、无源性、(Q,S,R)-耗散性等,更便于系统性能的分析,目前该概念已经被引入神经网络等问题的研究中[12-13]。
但增广耗散性能指标在切换系统中还少有研究,因此本研究将增广耗散性能指标的研究扩展到中立时滞切换系统,并分析系统的有限时间有界性。首先,给出问题陈述及相关引理,然后基于平均驻留时间以及线性矩阵不等式方法得到中立时滞切换系统有限时间有界且满足有限时间增广的耗散性性能指标的充分条件,最后给出相关结论并通过数值仿真实例验证方法的有效性。
1 问题描述
考虑下面带有时变时滞的中立切换系统:
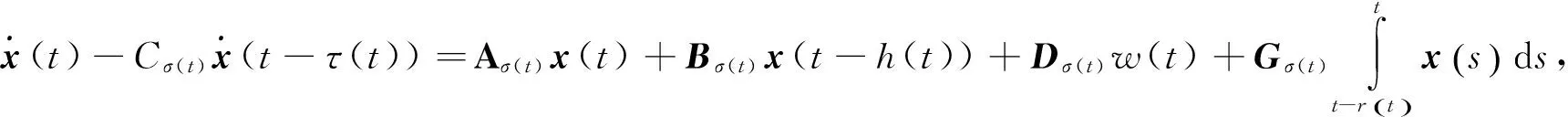
(1)
zt=Fσ(t)x(t) ,
(2)
x(θ)=φθ,∀θ∈-τ,0。
(3)

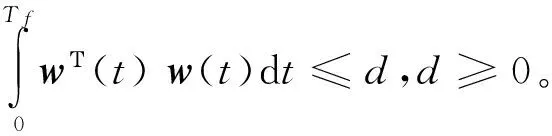
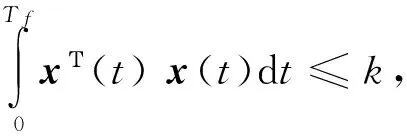
假设3矩阵ψ3,ψ4满足以下条件:
2) ‖ψ1‖+‖ψ2‖‖ψ4‖=0。
假设4对∀α≥0,μ≥1,∀t∈0,Tf,有eαtμNσ(0,t)≤b,Nσ(0,t)代表σ(t)在0,t区间上的切换次数,b为正的常数。
定义111对给定的矩阵ψ1,ψ2,ψ3和ψ4满足假设3,当初始状态x(0)=0,系统(1)、(2)具有增广的耗散性,如果对任意的Tf≥0及w(t)∈L20,∞以下的不等式成立:
(4)
其中:
J(t)=zΤ(t)ψ1z(t)+2zΤ(t)ψ2w(t)+wΤ(t)ψ3w(t)。
在定义1中,通过调整矩阵参数,增广的耗散性涵盖了一些著名的性能指标:
1)L2-L∞性能指标:ψ1=0,ψ2=0,ψ3=γ2I,ψ4=I;
2)H∞性能指标:ψ1=-I,ψ2=0,ψ3=γ2I,ψ4=0;
3) 无源性:ψ1=0,ψ2=I,ψ3=γI,ψ4=0;
4) (Q,S,R)-耗散性:ψ1=Q,ψ2=S,ψ3=R-βI,ψ4=0。
定义210给定三个常数c1,c2,Tf且c1 (5) 成立,若w(t)=0,则称为有限时间稳定的。 定义310对任意T2>T1≥0,Nσ(T1,T2)代表σ(t)在时间区间T1,T2上的切换次数,如果 对于τa>0和整数N0≥0都成立,则τa称为平均驻留时间。 N0为扰动界,不失一般性,本文取N0=0。 引理114X,Y为适当维数的实向量,则2XΤY≤XΤX+YΤY成立。 引理214对正定矩阵N∈Rn×n,标量τ>0和向量函数x·:R→Rn,积分不等式 定理1考虑系统(1)~(3),令对给定正的标量rm,如果存在适当维数的对称正定矩阵Ni,以及适当维数的矩阵X11i,X12i,X22i,H1i,H2i使得 (6) (7) 其中, (8) 成立,同时, λ2+hmeαhmλ3+τmeατmλ4+hmeαhmλ5+rmeαrmλ6c1+λ7d (9) 进一步,平均驻留时间满足: (10) 其中 λmin(Pi)=λ1,λmax(Pi)=λ2,λmax(Qi)=λ3,λmax(Zi)=λ4,λmax(Ti)=λ5,λmax(Mi)=λ6,λmax(Ni)=λ7。 (11) 且μ>1满足 (12) 则切换系统(1)~(3)基于c1,c2,Tf,d,R,σ是有限时间有界的。 证明选取候选李雅普诺夫函数为 V(t)=Vσ(t)(t)=Vi(t)=V1i(t)+V2i(t)+V3i(t)+V4i(t)+V5i(t)。 基于系统(1)~(3)对V(t)求导得: 由牛顿-莱布尼茨公式得: 显然成立。 又因为 其中, 由引理2得 因此,在状态xt≠0的条件下,由式(7)~(8)得 (13) 积分式(13),由式(12)~(13)得对∀t∈tk,tk+1, (14) 由定义3得: (15) 另一方面, (16) ≤[λmaxPi+hmeαhmλmaxQi+τmeατmλmaxZi+hmeαhmλmaxTi+rmeαrmλmaxMi] ≤λ2+hmeαhmλ3+τmeατmλ4+hmeαhmλ5+rmeαrmλ6c1。 (17) 由式(15)~(17)得 (18) 当μ=1,由式(9)得 xΤ(t)Rx(t) 当μ>1,由式(9)得 ln(λ1c2)-lnλ2+hmeαhmλ3+τmeατmλ4+hmeαhmλ5+rmeαrmλ6c1+λ7d-αTf>0 由(10)得 (19) 把式(19)代入式(18)得 证毕。 推论考虑系统(1)~(3),令w(t)对给定正的标量rm,存在适当维数的正定对称矩阵以及适当维数的矩阵X11i,X12i,X22i,H1i,H2i使得 λ2+hmeαhmλ3+τmeατmλ4+hmeαhmλ5+rmeαrmλ6c1 其中λ1,λ2,λ3,λ4,λ5,λ6满足式(11),μ>1 满足式(12)。 其中, 成立,当平均驻留时间满足 时,切换系统(1)~(3)基于c1,c2,Tf,R,σ(t)是有限时间稳定的。 证明证明过程与定理1相似。证略。 定理2考虑系统(1)~(3),令对给定正的标量rm,存在适当维数的正定对称矩阵以及适当维数的矩阵X11i,X12i,X22i,H1i,H2i使得 (20) (21) (22) 其中, (23) (24) 平均驻留时间满足 (25) 则系统满足增广的耗散性性能指标且基于0,c2,Tf,d,R,σ(t)是有限时间有界的。 证明与定理1的证明相似,可得: 其中, 由式(22)~(23)得: 在零初始状态V(0)=0下,得 因此 由假设4得 所以 考虑不等式 若ψ4>0,由假设3得ψ1=0,ψ2=0,ψ3>0,所以 因此对∀ 由(20)有 得 因此增广的耗散性证明完成,以下证明有限时间有界,由以上证明得 从而 又因为ψ1≤0,所以 由以上不等式得 则 又因为 则由式(25)得xΤ(t)Rx(t) 考虑两个子系统的情况,令系统(1)~(2)的参数为 以上仿真结果表明,存在相应的矩阵使得相应的矩阵不等式成立,系统有限时间有界与增广的耗散性成立,从而验证了方法的有效性。 运用平均驻留时间及线性矩阵不等式方法分析了系统有限时间有界与增广的耗散性问题,基于增广的耗散性概念,将H∞,L2-L∞,无源性,(Q,S,R)-耗散性指标整合到一个统一的框架,使得系统性能的分析更加方便。用线性矩阵不等式方法可使仿真结果验证更加便利。未来增广的耗散性概念将会应用到更多复杂动态系统中。 参考文献: [1]LIN H,ANTSAKLIS P J.Stability and stabilizability of switched linear systems:A survey of recent results[J].IEEE Transactions on Automatic Control,2009,54(2):308-322. [2]付主木,费树岷,高爱云.切换系统的H∞控制[M].北京:科学出版社,2009:21-43. [3]胡柯.切换系统稳定性及时滞相关问题的研究[D].上海:上海交通大学,2008:12-34. [4]程代展,郭宇骞.切换系统进展[J].控制理论与应用,2005,22(6):954-960. CHENG Daizhan,GUO Yuqian.Develepment of switched systems[J].Control Theory and Applications,2005,22(6):954-960. [5]孙文安.几类线性切换系统的鲁棒控制[D].沈阳:东北大学,2005:52-64. [6]ZHANG Y,LIU X,ZHU H,et al.Stability analysis and control synthesis for a class of switched neutral systems[J].Applied Mathematics & Computation,2007,190(2):1258-1266. [7]LIU D,ZHONG S,LIU X,et al.Stability analysis for uncertain switched neutral systems with discrete time-varying delay:A delay-dependent method[J].Mathematics & Computers in Simulation,2010,80(2):436-448. [8]XIANG Z,SUN Y,Mahmoud M S.Robust finite-timeH∞control for a class of uncertain switched neutral systems[J].Communications in Nonlinear Science & Numerical Simulation,2012,17(4):1766-1778. [9]ORLOV Y.Finite time stability and robust control synthesis of uncertain switched systems[J].SIAM Journal of Control and Optimization,2005,43(4):1253-1271. [10]LIN X Z,DU H B,LI S H.Finite-time boundedness andL2-gain analysis for switched delay systems with norm-bounded disturbance[J].Applied Mathematics & Computation,2011,217(12):5982-5993. [11]ZHANG B Y,ZHENG W X,XU S Y.Filtering of Markovian jump delay systems based on a new performance index[J].IEEE Transactions on Circuits & Systems I Regular Papers,2013,60(5):1250-1263. [12]XIAO J Y,LI Y T,ZHONG S M,et al.Extended dissipative state estimation for memristive neural networks with time-varying delay[J].ISA Transactions,2016,64:113-128. [13]YANG H L,SHU L,ZHONG S M,et al.Extended dissipative exponential synchronization of complex dynamicalsystems with coupling delay and sampled-data control[J].Journal of the Franklin Institute,2016,353(8):1829-1847. [14]俞立.鲁棒控制-线性矩阵不等式处理方法[M].北京:清华大学出版社,2002:241-269. [15]吴敏,何勇.时滞系统鲁棒控制[M]北京:科学出版社,2008:66-92.
2 主要结果
2.1 有限时间有界分析




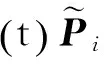
2.2 有限时间增广的耗散性分析
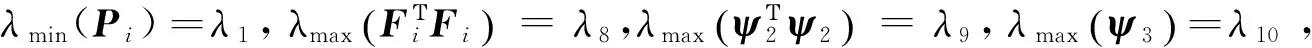

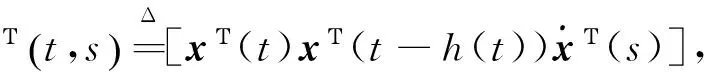


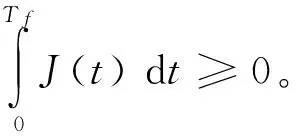
3 仿真实例
4 结论

