基于遗传算法优化的WSN覆盖控制算法
李向峰,席志红,李 爽
(1.哈尔滨工程大学 信息与通信工程学院,黑龙江 哈尔滨 150001;2.卫星导航系统与装备技术国家重点实验室,河北 石家庄050081)
0 引言
随着通信技术、嵌入式软件技术和传感器技术的高速发展与应用,WSN已经发展到第四代技术[1],作为物联网的关键组成部分,已经广泛应用于军事领域、环境监测、自然灾害预报、医疗健康和智能家居等领域[2-4]。覆盖控制是影响整个网络服务质量、感知信息能力、网络能耗和寿命的直接因素。因此,降低因为节点电池耗尽而出现的网络区域覆盖漏洞,高效利用节点能量和延长网络生命周期保障监测区域的有效覆盖是无线传感器网络十分重要的研究课题[5]。
无线传感器网络有效覆盖控制是保障服务质量(QoS)的首要条件,在部署节点时通常会使用冗余节点来保障目标区域的完全覆盖,这就形成了k重覆盖问题[6]。文献[7]使用文化基因(Memetic)算法产生平衡簇来均衡每个节点的能量消耗,避免覆盖漏洞过早出现,但是使用了部分移动节点,并没有考虑节点运动所消耗的附加能量[8-10]。文献[11]基于(m,k)-Gur Game算法改进的休眠策略,通过交替性地休眠唤醒节点均匀节点能耗,避免某些节点过度使用提前死亡造成覆盖漏洞,但是其仍然没有避免WSN网络产生大量冗余数据。
本文基于Memetic算法框架结构对遗传算法(Genetic Algorithm,GA)进行改进,在遗传算法的基础上结合针对WSN提出的局部搜索策略(Local Search Algorithm,LSA)进一步优化算法性能,尽可能使用最少的节点保障监测区域的完全覆盖。本文算法中遗传操作主要完成种群迭代评估覆盖率,局部搜索算法在保障覆盖率不下降的同时进一步减小需要激活的节点数量,提高适应度。
1 网络模型和相关理论
假设普通节点、汇聚节点和监测目标点(Monitored Target Points,MTP)在部署之后都是静止的,节点都是同构类型,它们具有相同的初始能量、数据处理能力和感知半径。当MTP在某个节点感知半径范围Rs内时,则认为该节点可以监测到此MTP,如图1所示,每一个MTP都至少被一个节点覆盖。为了简化实验复杂性,本文使用文献[12]中研究测试的感知半径范围Rs为17.675 m。节点将监测到的数据发送给簇、头,簇、头接收到数据后再通过直接发送或者多跳的方式发送给汇聚节点[13-14]。
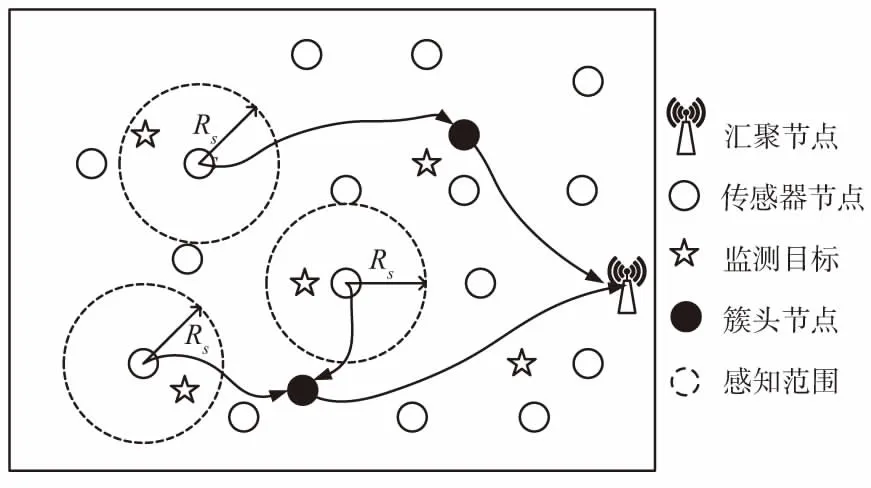
图1 无线传感器网络模型
1.1 感应覆盖模型
基于二元感知模型构建WSN的感知覆盖模型,将传感器节点定义为S={s1,s2,s3,…,sN},N为节点总数。监测目标定义为T={t1,t2,t3,…,tM},M为MTP的数量。定义MTP二进制覆盖变量Gi,j为:
(1)
式中,E为节点si当前能量,当si和tj之间的距离小于等于Rs时,则tj被si所监测,令Gi,j=1。当tj在v个节点时,定义Tj表示目标监测节点tj是否被监测,当Tj=1时,表示tj被监测。
Tj=G1,j∪G2,j∪…∪Gv,j。
(2)
集合覆盖问题(Set Covering Problem,SCP)是经典的NP-Complete问题,SCP调度节点使某一组传感器节点保障目标区域中每一个MTP都至少被一个节点所监测。SCP数学描述如下:

(3)
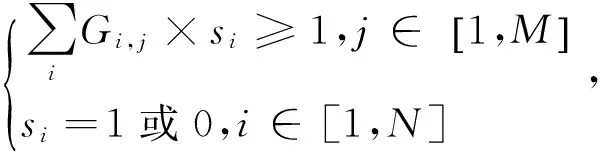
(4)
式中,cost(i)表示激活节点si的成本代价,用si=1表示节点处激活状态,si=0表示处于休眠状态。式(3)表示在最优状态下,激活使用最少的节点,以达到代价成本最低,但是其受式(4)的约束,必须保证每一个MTP都至少被一个节点所覆盖。求解SCP问题的过程就是上述2个公式相互制约、互相博弈的过程。
1.2 遗传算法
在进行遗传操作之前首先要得到一个初始种群,为了得到初始种群,根据遗传算法的相关理论进行如下定义:
定义1 基因(Gene):传感器节点si的取值称为一个基因或者等位基因,为了方便算法的实施采用二进制编码。si=1表示传感器节点处于激活状态;si=0表示传感器节点处于休眠状态。
定义2 染色体(Chromosome):将若干基因的集合称为染色体或者个体,使用二进制字符串表示。假设在区域内分布N个传感器节点,则这N节点的二进制编码构成一个染色体。
定义3 种群(Population):在同一区域内若干同类个体构成种群,在初始种群的基础上进行遗传操作得到新一代的种群,它是进化的基本单位。
第一代初始种群采用随机产生方法生成,每一个节点在初始时随机地选择激活或者休眠状态,所以理论上处于激活和休眠状态的节点数量各占一半。一个种群模型示例如图2所示,根据定义1,基因li,j表示染色体i中第j个节点sj的状态,li,j为1表示节点sj激活状态,为0表示休眠,每个染色体的长度为N。
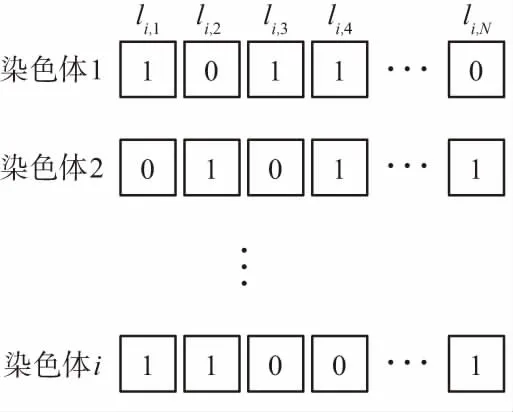
图2 种群模型示例
根据上述初始节点取值和染色体的定义可知,每一个染色体的编码都由一串二进制代码组成。染色体编码示例如图3所示,假设共有15个传感器节点用于感测7个目标监测点MTP,显然图中存在k重覆盖问题,通过遗传算法操作可以达到激活最少数量的节点覆盖所有监测点。这里使用9个节点(s1,s3,s7,s8,s9,s12,s13,s14,s15)就可以覆盖所有的7个监测点,剩下的6个(s2,s4,s5,s6,s10,s11)为冗余节点。根据上面定义的基因模型,就可以方便地将图3中给出的示例染色体用二进制字符串“101000011001110”来表示这15个等位基因{l1,1,l1,2,l1,3,l1,4,l1,5,l1,6,l1,7,l1,8,l1,9}的编码。
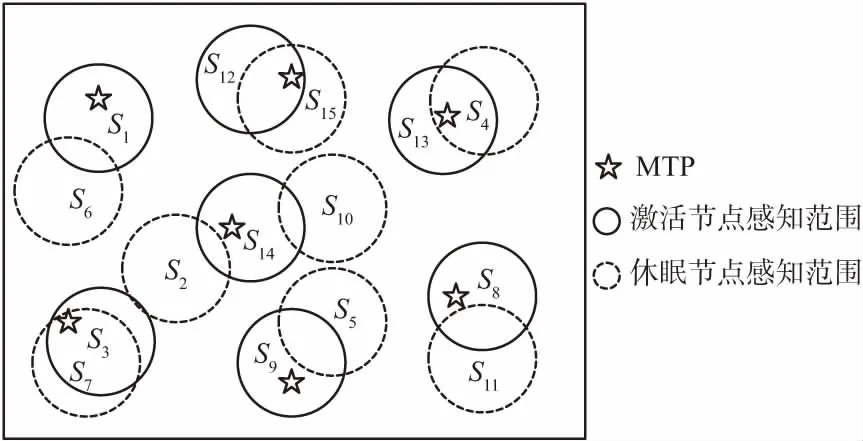
图3 染色体编码示例
1.3 选择、交叉、变异运算
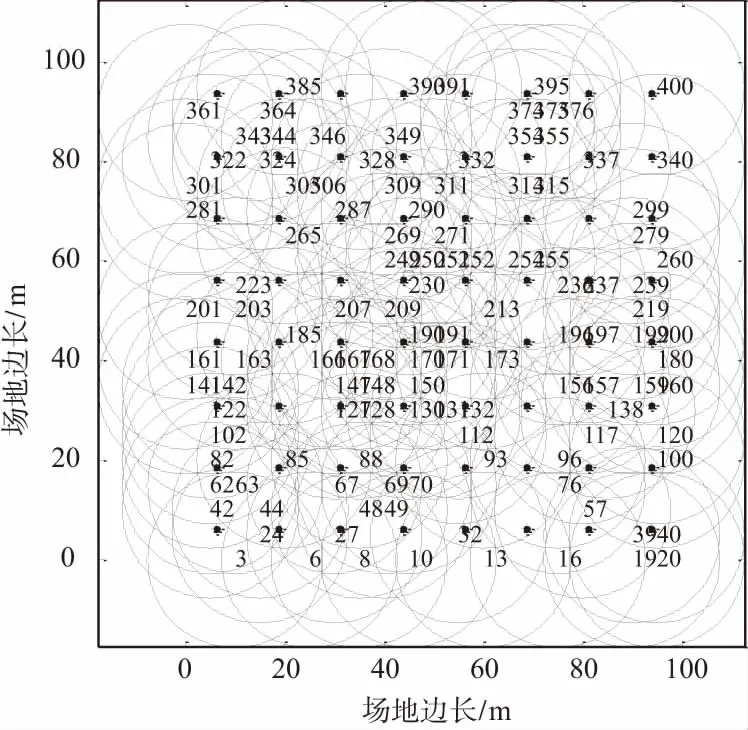
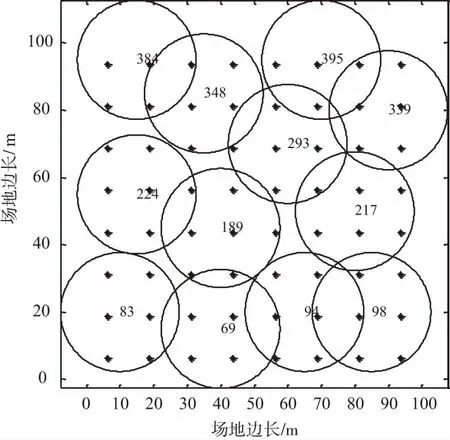
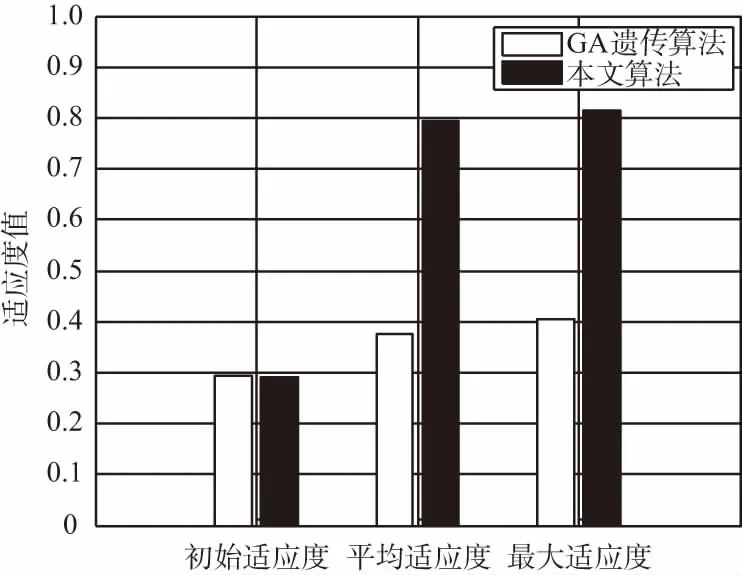
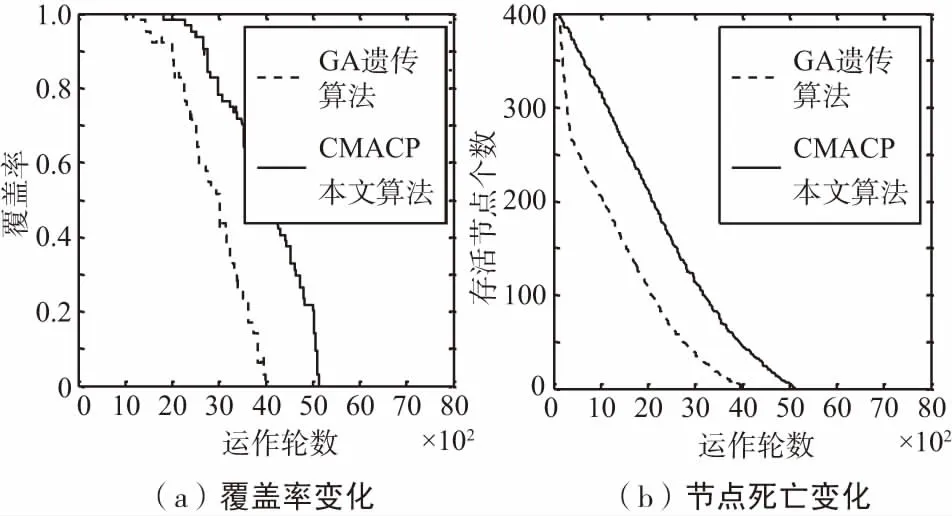
遗传算法包含选择、交叉和变异,通过多次种群选择迭代减少冗余节点来提高适应度。选择过程可以得到较好的复制品,但是不能产生新的个体,为了保持种群的多样性,提高遗传质量,必须引入新的个体。交叉操作是模仿生物的交配繁殖过程,确定适当的交叉率很重要。以交叉率Rc(0 图4 交叉操作示意 首先改进遗传算法适应度函数,然后根据Memetic文化基因算法框架结构提出局部搜索策略,最后在遗传算法的基础之上结合局部搜索策略构成本文算。 适应度值的大小是遗传操作中选择个体的重要指标[19]。本文算法的目标是激活使用尽可能少的节点来实现最佳覆盖率。对于每个节点,用覆盖向量ci表示某一个特定节点si对每一个MTP的覆盖情况,ci=[Gi,1,Gi,2,…,Gi,M],其中si∈S。同样,对于另一个传感器节点sj∈S,覆盖向量cj表示为cj=[Gj,1,Gj,2,…,Gj,M],i≠j。通过布尔或运算,可以得到节点si和sj的综合覆盖变量ω(si,sj)定义为: ω(si,sj)= [ci∪cj]= (5) 用ω(si,sj)来确定每个MTP是否被节点si或者sj覆盖。因此,推广到某一个染色体k的综合覆盖向量ω(k)定义如下: ω(k)=(lk,1c1)∪(lk,2c2)∪…∪(lk,NcN)。 (6) 将式(5)代入式(6)得: (7) 通过将覆盖评估过程简化为二进制操作,可以大幅简化CMACP协议计算的复杂性。可以通过以下公式计算染色体k的覆盖率: (8) 式中,‖ω(k)‖表示染色体k覆盖的MTP数量。则染色体k的节点利用率可以通过以下公式计算: (9) f(k)=α1×(‖ω(k)‖)τ1-α2×(μ(k,s))τ2。 (10) 将式(8)和式(9)的染色体k覆盖MTP数量ε(k)和节点利用率μ(k,s)代入式(10)得: (11) 式中,α1和α2是加权系数;τ1和τ2是指数因子。由式(11)可以得到适应度函数f(k)随着ε(k)的增大或μ(k,s)减少而增大,显然,覆盖MTP数量越多并且使用的节点数量越少则适应度越高,满足SCP所描述的最佳模型式(3)和约束条件式(4)。如果染色体k具有较高的适应度值,则意味着其可以激活使用更少的节点来监测比其他染色体更多的MTP目标。在遗传操作的过程中,每个染色体需要通过适应度函数进行计算排序,按照排序保留适应度最大的种群作为下一代的父本。通过适应度函数选择精英种群,经过数代的迭代后将得到一个覆盖率最大和适应度较高的种群。 Memetic算法中的局部搜索策略就有很高的灵活性,可以和不同的搜索策略相结合。基于无线传感器网络的特点和本文构建的二进制模型,改进了一种能优化染色体适应度的搜索策略。每一代染色体的遗传操作完成后,通过局部搜索策略进一步提高染色体适应度。局部搜索算法的伪代码描述如下: 本地搜索策略:步骤1:输入种群Popk={chrom1,chrom2,…,chrompop_size}k,pop_size为种群大小。步骤2:设chromi是种,群Popk中第i-th的个体,N为chro-mi的长度。根据等位基因li,j定义可知,染色体chromi是由等位基因li,j组成的二进制字符串。∀i,1≤j≤N.Fori=1topop_sizedo Forj=1toNdo ∥记录值为1的等位基因 Ifthevalueofli,jisequaltoonethen Recordthealleleli,jinthearraysi. End EndEnd步骤3:Fory=1topop_sizedoLethbethelengthofSy.Forl=1tohdo fitness1=fit(chromy); Inchromy,lettheallelelv,htobezeroinSy.∥将等位基因置零 fitness2=fit(chromy); Iffitness1>fitness2then Letlv,hequaltoone. EndEndEnd步骤4:输出最佳解种群Popk 该策略将每个等位基因li,j的值从1变为0,如果改变后覆盖率不变则保留这个改变,如果覆盖率下降则恢复。局部搜索方案遍历所有的等位基因,尽可能地提高个体的适应度,并通过比较原始染色体和新染色体的适应度大小来确定是否保持修改。运行局部搜索策略后可以得到一个比原先适应度更高(至少等于)的种群。 其中Popk是具有pop_size个染色体的一个种群,chromi是种群中的一个染色体。令f(k)previous=fitness1,f(k)current=fitness2,经过局部搜索算法操作后,必然有f(k)previous≥f(k)current。搜索算法计算后可以得到新的适应度值f(k): f(k)=max{f(k)previous,f(k)current}。 (12) 运行遗传算法和局部搜索策略后,可以得到初始激活节点集合Pactive和休眠节集合Psleep。CMACP算法可以通过执行局部搜索过程获得更好的结果,加速算法收敛过程。 综上所述,改进的遗传算法的适应度函数结合局部搜索构成本文算法,算法流程图如图5所示。 图5 本文算法流程 本文算法的设计思路是在遗传算法进行每一代的迭代后添加局部搜索策略对种群进一步优化。通过局部搜索策略对每一个等位基因进行搜索,寻找遗传算法中遗漏未优化的冗余节点。如果发现冗余节点则对节点进行优化,进一步提高种群适应度,如此往复运行直到满足适应度终止标准或者达到最大迭代次数进化过程终止适应度最大的种群为最优解。 本文仿真环境使用Matlab 8.1[20-21]平台,设置在大小为100 m×100 m的区域内部署400个传感器节点和64个MTP。通过与遗传算法对比来测试局部搜索算法对提高适应度的有效性,根据本文算法处理流程,首先每一次迭代中先由遗传算法得到一个初始种群,然后局部搜索算法负责进一步优化种群适应度后完成一次迭代,从中选出精英种群作为母本,最后经过多次迭代后得到一个较为理想的种群。遗传算法和本文算法运行前节点和MTP的分布情况如图6、图7和图8所示,分别表示经过遗传算法和本文算法迭代40代后得到的最优初始种群覆盖情况。 其中,数字表示传感器节点序号,“○”表示节点的感知范围,“*”表示 MTP监测点。从图7和图8中可以得出遗传算法在初始覆盖时使用的节点数量明显比本文算法更多,说明遗传算法的适应度并不高,选择出的种群不是最优种群,进一步对比分析二者的适应度同样验证了这一结论,图9对比了2种算法的初始适应度、平均适应度和最大适应度值。 图6 400个节点,64个MTP均匀分布 图7 遗传算法40次迭代后初始覆盖 图8 本文算法40次迭代后初始覆盖 图9 GA算法和本文算法适应度值对比 在算法运行迭代之前,二者的初始适应度值几乎相同,经过40次种群迭代之后,不论是平均适应度还是最大适应度,有局部搜索算法的本文算法都要比没有的遗传算法的适应度值都要高出近一倍。更高的适应度必然在网络寿命和覆盖率上有更好的表现,图10对比了2种算法的覆盖率和节点死亡的变化情况。 图10 GA算法和本文算法覆盖率和节点死亡变化对比 图10(a)显示CAMCP算法比遗传算法维持100%覆盖MTP运行的轮数更多,分别为1 815轮和1 166轮,100%覆盖轮数提高了55.66%,整体网络寿命分别为5 134轮和3 984轮,网络寿命提高28.87%。从图10(b)中可以看出,遗传算法的节点死亡速度更快,这是因为遗传算法的适应度并不高,仍然有冗余节点处于激活工作状态,它们做重复性工作的同时也在消耗能量。从以上分析中可以得出,本文算法可以有效地进一步提高遗传算法的适应度,延长100%覆盖MTP的时间和网络整体寿命。 本文基于Memetic算法框架结构在遗传算法的基础上构建了无线传感器网络覆盖模型,结合局部搜索策略改进了遗传算法。通过分析遗传算法发现其存在过早收敛和适应度低的情况,并且为了保障初始覆盖率而大量布置的传感器节点造成了节点冗余,在WSN网络运行时冗余传感器节点又会产生大量的冗余数据进一步加重了WSN网络的数据处理负担增加能耗。本文算法针对提高遗传算法适应度和规划冗余节点2个方面进行优化,通过仿真实验对比得出,与遗传算法相比本文算法通过局部搜索将适应度值提高了近1倍,在保障100%覆盖 MTP同时使用更少的节点,节点规划更加合理,有效延长了100%覆盖时间和整体网络寿命。 [1] 陶志勇,蒋守凤.基于模糊理论的无线传感器网络簇首选举算法[J].计算机工程,2015,41(9):115-119. [2] 肖发远,李好威.基于模糊理论的无线传感器网络路由优化算法[J].广西师范大学学报,2017,35(1):37-43. [3] 曾东,熊飞.面向能耗控制的无线传感器网络节点协议优化[J].无线电通信技术,2014,40(1):28-31. [4] 熊炼,叶建光,刘晓彤.基于动态簇半径的非均匀分簇算法[J].无线电通信技术,2017,43(1):51-55. [5] 徐晶晶,张欣慧,许必宵.无线传感器网络分簇算法综述[J].计算机科学,2017,44(2):31-37. [6] MEENAKSHI Y,DANIEL A K.Performance Analysis of Approaches for Coverage Issues in WSN[C]∥2016 International Conference on Computing for Sustainable Global Development (INDIACom),2016:782-787. [7] MASOOD A,ATAUL A I,ISHTIAQ W,et al.A Memetic Algorithm Approach to Clustering inMobile Wireless Sensor Networks[C]∥Future Technologies Conference,2016:936-940. [8] 汤杰,郑霖.能耗均衡的无线传感网络不等环分层路由算法[J].无线电工程,2017,47(10):12-16. [9] XIAOHUI Y,MOHAMED E,HAMDY K E.Genetic Algorithm-based,Dynamic Clustering Method Towards Improved WSN Longevity[C]∥Journal of Network and Systems Management,2016:1-26. [10] 戚玉涛,刘芳,常伟远.求解多目标问题的 Memetic免疫优化算法[J].软件学报,2013(7):1529-1544. [11] TIAGO S,CARLOS M,PAULO P A.Sleep-scheduling Scheme for Enhancing QoS and Network Coverage in IEEE 802.15.4 WSN[C]∥Factory Communication Systems,2015:1-4. [12] GAO Y,WKRAM C H,Duan J,et al.A Novel Energy-aware Distributed Clustering Algorithm for Heterogeneous Wireless Sensor Networks in the Mobile Environment[J].Sensors,2015,15(12):31108-31124. [13] 马箫雯,余翔,许未.基于LEACH的WSN路由算法研究[J].无线电通信技术,2013,39(2):14-16. [14] 孔令荣,王昊,庄涛.基于WSN的分簇路由协议研究与改进[J].无线电工程,2014,44(12):48-51. [15] SRINIVAS M,PATNAIK L M.Adaptive Probabilities of Crossover and Mutation in Genetic Algorithms[J].IEEE Transactions on Systems Man & Cybernetics,2002,24 (4):656-667. [16] EIBEN A E,MICHALEWICZ Z,SCHOENAUER M,et al.Paraeter Control in Evolutionary Algorithms[J].In Parameter Setting in Evolutionary Algorithms,2007,54:19-46. [17] 周杰.基于进化算法的大规模无线传感器网络覆盖关键技术研究[D].北京:北京邮电大学,2015. [18] 祁育仙.基于遗传算法的无线传感器网络覆盖控制研究[D].太原:太原理工大学,2015. [19] YUAN Xiaohui,MOHAMED E,HAMDY K,et al. A Genetic Algorithm-Based,Dynamic Clustering Method Towards Improved WSN Longevity[J].Journal of Network and Systems Management,2017,25(1):21-46. [20] 薛定宇,陈阳.泉高等应用数学问题的MATLAB求解[M].北京:清华大学出版社,2008:264-325. [21] 莫勒,喻文健.MATLAB数值计算(2013修订版)[M].北京:机械工业出版社,2013:462-511.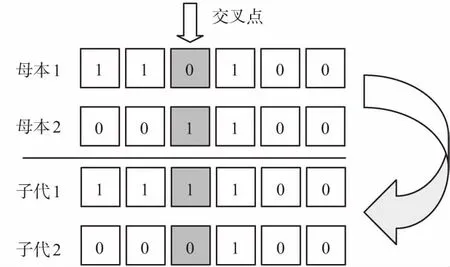
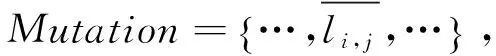
2 改进遗传算法
2.1 适应度函数
[Gi,1∪Gj,1,Gi,2∪Gj,2,…,Gi,M∪Gj,M]。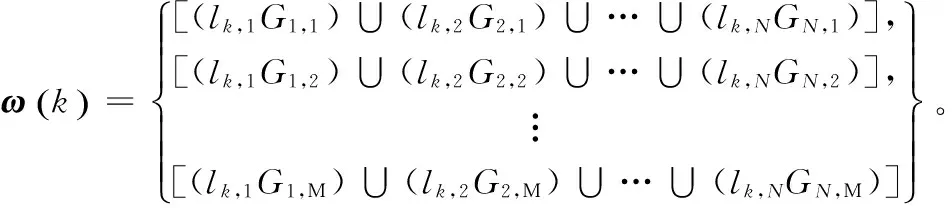

2.2 局部搜索策略

2.3 本文算法流程

3 仿真实验及结果分析

4 结束语

