一类准零刚度橡胶隔振器研究

黎瑞和，王国砚,吴 同,2，朱金龙

（1.同济大学 航空航天与力学学院，上海 200092；2.中建二局第一建筑工程有限公司，北京 100176）

在许多工程领域，常遇到需要隔振、减振的问题。根据振动理论[1]，基于被动控制理论的隔振系统只有当外部环境的干扰激励频率高于隔振系统固有频率的倍时才有隔振效果。因此，低频隔振是隔振技术研究领域面临的热点问题之一，目前的研究热点是准零刚度隔振系统的研制。研究者们普遍认为，准零刚度能解决低频隔振中常遇到的固有频率低与静位移大之间的矛盾。

准零刚度的实现是通过正负刚度弹性元件的并联，最初由Alabuzhev提出[2]。进入21世纪后，关于不同形式的准零刚度系统的研究非常多。归纳起来，主要有以下两种实现形式：一种是通过竖向和侧向弹簧组合，由Carrella于2006年提出[3]，在此基础上衍生出很多形式。例如，利用受轴压力的梁与正刚度弹簧组合[4]；利用5个线性弹簧[5]；通过滚球副来放大微幅振动对负刚度机构的敏感性[6]；利用水平磁力弹簧和竖直弹簧组合[7]。另一种是利用能产生失稳现象的板或薄壁结构。例如，由竖直橡胶垫和屈曲弹簧钢板组合而成准零刚度隔振器[8]；利用加筋碟形弹簧与竖直弹簧的组合[9]以及用聚氨酯制作的单个碟形橡胶隔振垫[10-11]。除此之外还有“剪刀”系统[12]和利用磁铁和弹簧的组合[13]等实现形式。

从所查阅的文献来看，目前关于准零刚度橡胶隔振器的研究大多只停留在理论阶段，且结构都比较复杂，因此可重复性是个问题。Anvar Valeev虽然声称用单个聚氨酯橡胶隔振器得到了固有频率低至1 Hz的系统，但是这个固有频率的计算仅仅通过刚度曲线获得[11]。本文设计了一个具有准零刚度特性的碟形橡胶隔振器，通过单轴试验获得橡胶材料的本构关系，通过静压试验获得力-位移曲线；通过刚度补偿拓宽了刚度曲线中的平缓段；对该隔振器进行单个和有刚度补偿下的振动试验，先通过快速扫频找到系统最优荷载，在此荷载下进行稳态振动试验，获得了低至4 Hz的固有频率，验证了该模型的有效性。最后利用ABAQUS很好地模拟了隔振器的静刚度曲线，证明了有限元建模的有效性。

1 单轴试验

1.1 单轴拉伸试验

单轴拉伸试验的试件采用的材料是邵氏硬度为60的天然橡胶（见图1(a)）。根据《GB/T528-2009硫化橡胶或热塑性橡胶拉伸应力应变性能的测定》[15]，试件中段标距长度为25.0±0.5 mm，宽度为7.0±0.7 mm，厚度为2.0 mm±0.2 mm。

在橡胶隔振器研究中先后4次定制了橡胶隔振器，因此同时定制了4批标准拉伸试件。为了避免偶然误差，每一批至少做3个试件。拉伸试验在INSRTON试验机（额定荷载为1 000 N，序列号80379）(见图1(b))上进行，试验的环境温度为23℃±3℃。

按照规范[15]和文献[16]的建议，取加载速率为12 mm∙min-1、120 mm∙min-1以及500 mm∙min-1。前后加工了4个批次的标准试验件。试件加工时间列于表1，所有标准试件的试验时间为2017年5月21日至26日。

图1 拉伸试件与试验装置

1.2 拉伸试验结果及分析

不同材料、不同加载速率工况下，单轴拉伸试验获得的名义应力-应变曲线如图2所示。

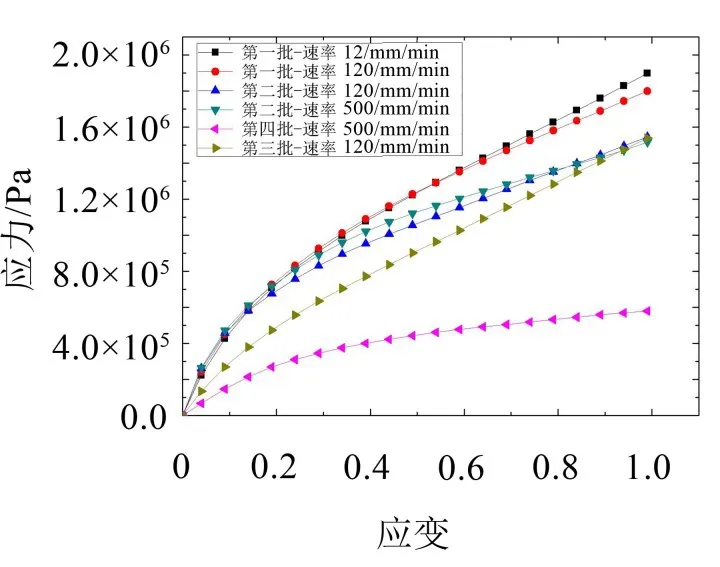
图2 不同材料、加载速率工况下的名义应力-应变曲线

由图可见，同一加载速率下（120 mm∙min-1）不同批次材料之间有较大不同。因此，针对每批次生产的橡胶隔振器都加工同一批标准试验件是非常必要的。

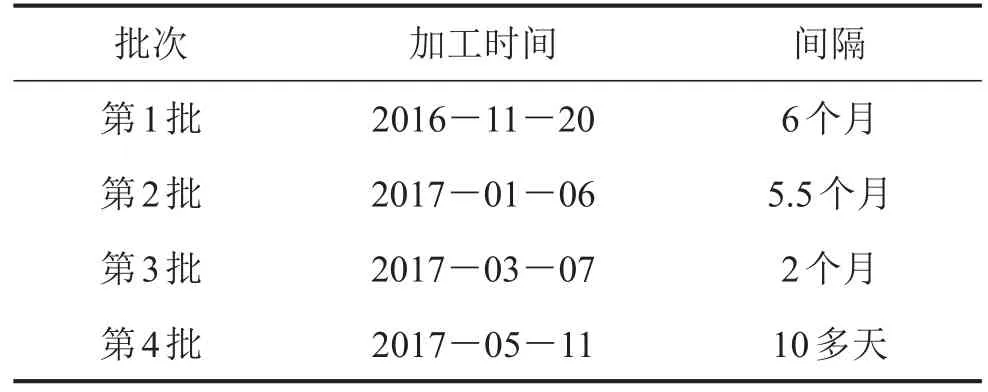
表1 不同批次橡胶拉伸件加工与试验时间的间隔

由图2看出，虽然不同批次的名义应力-应变曲线差距比较大，但更重要的是放置时间的不同所导致的同1批次的差异。第4批的试验时间距离加工时间只有10多天，在相同的应变下，其应力比最早加工的第1批材料要低将近1倍。因此，在研究中，为了保证隔振器的刚度实验和单轴拉伸试验的模拟能够与试验数据有较好的吻合度，必须使单轴拉伸试验和橡胶隔振器的静刚度试验进行的时间比较接近。

使用8项多项式对图2中的名义应力-应变曲线进行拟合，表达式如式(1)所示，式中应力单位为Pa。将第1、2批材料的前5项系数列于表2。

表2 第1、2批材料应力应变8次多项式关系拟合系数

1.3 单轴压缩试验

本文研究的橡胶隔振器主要承受压、弯荷载。在定制最后一批隔振器时，同时还定制了拉伸和压缩试验件。压缩试验在CSS42200万能试验机（最大荷载为20 t）上进行，根据规范《GB 7757-2009硫化橡胶或热塑性橡胶压缩应力应变性能的测定》[17]中的A法对应的标准试件，采用直径29.0±0.5 mm、高为12.5 mm±0.5 mm的圆柱体。试验在室温下进行，温度为27℃±5℃，以10 mm·min-1的速度压缩试样，直到应变达到25%为止。

用6阶多项式拟合得到压缩名义应力-应变关系，式中应力单位为Pa，如式(2)所示。

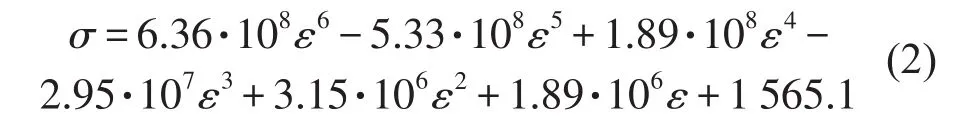
2 隔振器静刚度试验

静刚度试验在CSS42200万能试验机（最大荷载为20 t）上进行，加载速率为1 mm∙min-1。文中拟定的橡胶隔振器典型形状如图3所示。

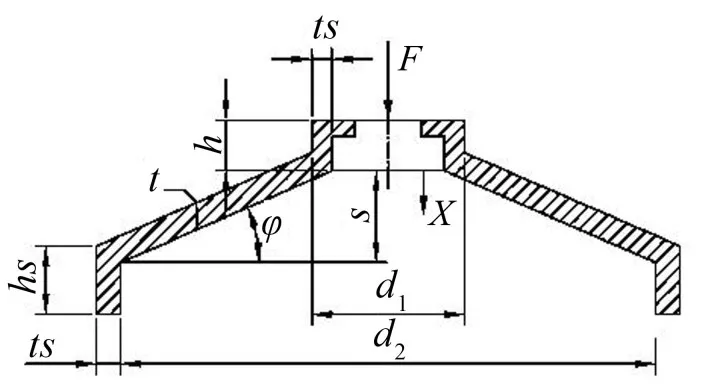
图3 橡胶隔振器尺寸

根据文献[16]，底直径d2、壁厚t、倾角φ是几个比较重要的尺寸。这些隔振器都采用邵氏硬度为60度的天然橡胶。具体尺寸见表3。其刚度实验结果见图4。

2.1 试验结果及分析

由图4可知，在受力初始阶段，橡胶隔振器能保持比较稳定的刚度，但随着位移的增加，倾斜的薄壁结构有被压曲的现象，到了一个临界位移时会呈现突然失稳的现象。由刚度曲线可以得到使隔振器刚度尽可能小的位移范围。因此，如果想利用单个隔振器进行隔振，必须至少满足以下两个条件：

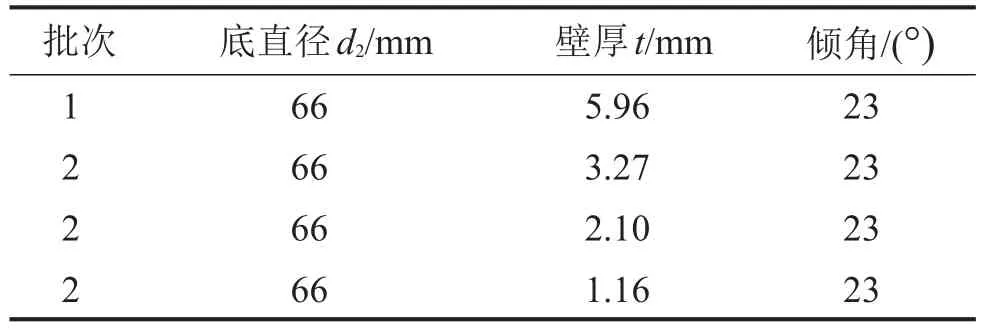
表3 第1、2批不同隔振器的尺寸

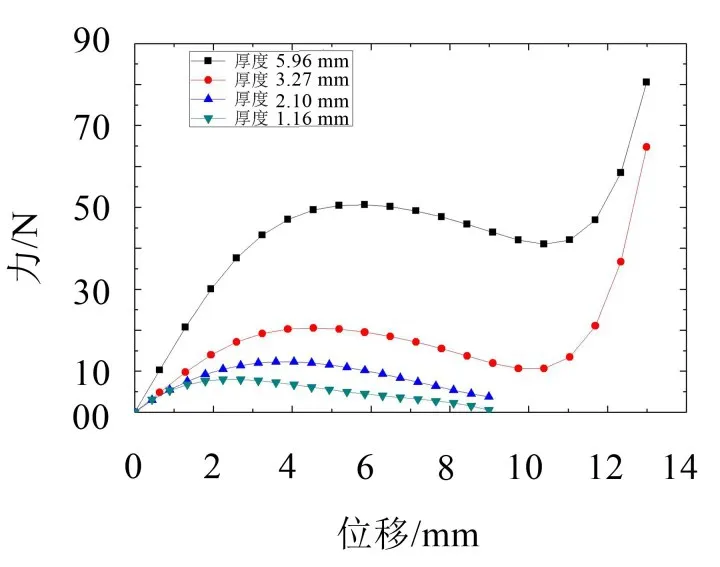
图4 不同厚度隔振器的力-位移曲线(d2=66 mm，φ=23 °)

(1)荷载使系统到达稍低于力-位移曲线最大值的位置，以保证较小的刚度；

(2)在此位置附近，系统做小幅振动，幅值不能使系统超过力-位移曲线的峰值。

综上所述，如果按照图3设计出的隔振器实现低频隔振，其振幅必定非常小，条件比较苛刻，有必要考虑进行刚度补偿，以保证系统的稳定性。

2.2 刚度补偿的影响

在本文研究中，采用金属小压簧放置于隔振器下方的形式来进行刚度补偿，如图5所示。

图5 刚度补偿示意图

以在上一小节中呈现较宽平缓段的底直径为66 mm、壁厚为3.27 mm、倾角为23°的隔振器为例说明刚度补偿过程与结果。本文采用3种不同的补偿方案，补偿效果如图6和表4所示。

由图6的力-位移曲线可以看出，不同方案中补偿后曲线显然更加平缓了。对于方案1，位移超过8 mm后曲线依次出现两个上升阶段，第1个上升阶段的斜率与隔振器刚被压缩时相差无几，是较矮的压簧发挥作用的区间；第2个上升阶段斜率较陡，是斜壁完全被压平后底部圆环提供刚度的区间，这个区间刚度太大，在振动过程中如果达到这个区间，对被隔振质量来说相当于受到一个冲击荷载，因此要注意避免。

以下定义低刚度范围∆x：对单个隔振器而言，∆x为刚度从1 N∙mm-1到0 N·mm-1的区间（因为刚度降到零后会失稳，需要避免）；对有补偿的弹簧而言，∆x为刚度曲线两次达到1 N∙mm-1对应的位移值之差。∆x的结果列于表4。

由表4可知，不同的补偿方案都起到了降低负刚度值、扩宽低刚度范围的作用。其中方案1具有宽达6.19 mm的刚度，低于1 N∙mm-1的区间，且最低刚度仅为0.115 6 N∙mm-1，做到了较大范围内的低刚度。

3 刚度实验的模拟

考虑到橡胶隔振器涉及材料非线性、几何非线性等非线性问题，本文采用ABAQUS等软件对其进行数值模拟。

3.1 有限元模型及参数设置

刚度实验的有限元模型如图7所示。模型底面及以上2 mm的侧面采用完全固定边界，以模拟刚度实验中502胶水的粘接。采用位移加载，通过将顶面处的参考点与顶面耦合在一起，通过参考点对顶面施加均匀的向下位移，再提取参考点处的支座反力，从而获得力-位移关系。静力分析步步长为1，最大步长增量为0.05，这样保证有20帧的数据，能够画出一条比较精确的曲线。单元类型选择为C3D8RH，单元数为10 000。在定义橡胶参数时输入单轴试验所得的名义应力应变关系，超弹性材料模型选为MARLOW，泊松比取为0.499。

图6 隔振器补偿前后的结果(d2=66 mm，t=3 mm，φ=23 °)

表4 不同补偿方案的效果

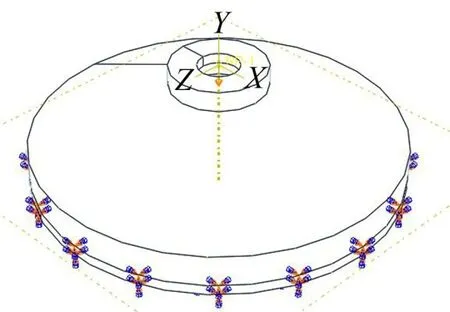
图7 隔振器静刚度有限元模拟示意图

3.2 数值模拟结果及分析

有限元模拟得到的力-位移曲线及与刚度试验中得到的相应曲线的比较如图8所示。

从图8中可以看出，数值模拟结果与实验结果具有较好的吻合度。

数值模拟得到的位移与实验结果之间的相对误差如图9所示。

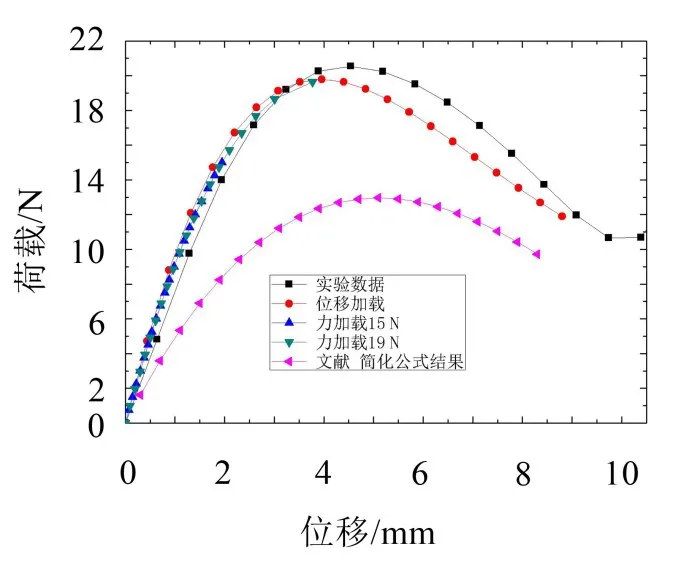
图8 橡胶隔振器力-位移曲线(d2=66 mm，t=3 mm，φ=23 °)

由图9可见，在位移较小时，相对误差较大，但在位移值达到2 mm之后，相对误差小于10%。而本文研究中隔振器达到准零刚度的区域，都在位移值为2 mm之后。换言之，有限元计算结果能够较好地模拟出在所关心的位移范围内的静刚度情况。

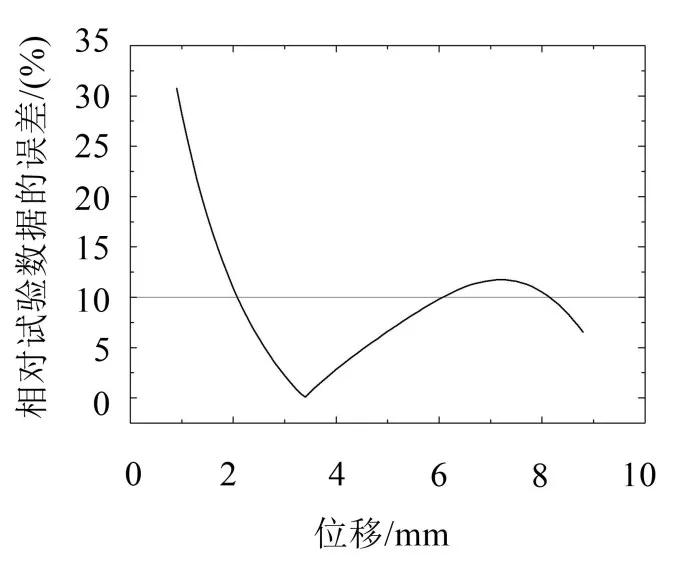
图9 有限元结果的误差分析

此外，图8中还给出了按照文献[16]中公式（见式（3）所示的橡胶力-位移计算公式)所得的结果。其中，弹性模量E=1.313 MPa，为拉伸应变为1时对应的原点割线弹性模量。

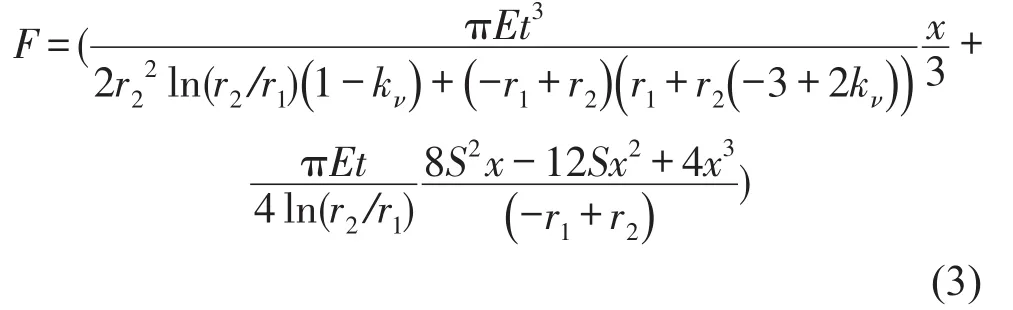
由图8可见，由式(3)给出的力-位移曲线无论是与实验结果比较还是与数值模拟结果比较，都有一定的误差；但该公式能表现一定的趋势，因此可以用于前期设计。

3.3 基于单轴压缩实验数据的数值模拟

上一节数值模拟中建立橡胶本构关系时采用的是单轴拉伸实验数据，为了比较采用拉伸试验数据和采用压缩试验数据对数值模拟结果的影响，本文针对第4批隔振器同时制作了拉伸和压缩试件并做了单轴拉伸和压缩试验。在保持上小节中材料参数设置基础上分别将拉伸和压缩的实验数据导入ABAQUS进行计算，计算结果和试验结果的比较如图10所示。

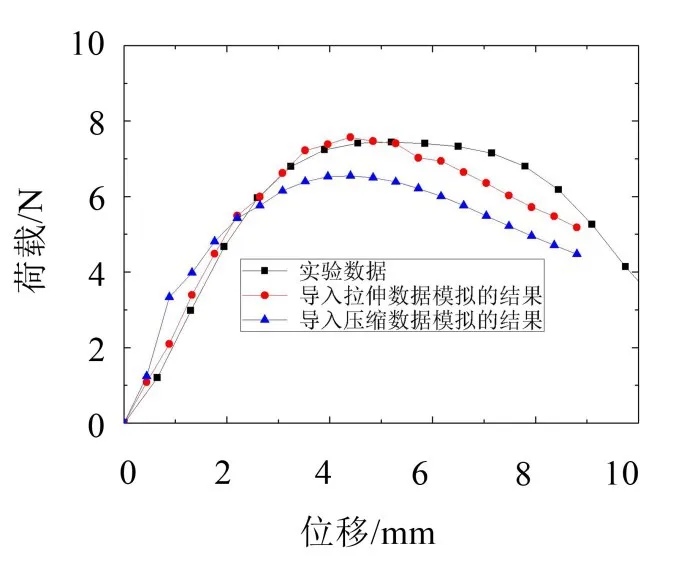
图10 基于单轴压缩实验数据的数值模拟

从图10中可以看出，在峰值之前，导入拉伸实验数据算得的力位移曲线几乎与实验数据重合，而导入压缩实验数据的力位移曲线虽然在1 mm～3 mm处与实验数据较为吻合，但与基于拉伸数据的结果相比精度还是不足。而在过了峰值后，基于拉伸和压缩数据的模拟结果与实验数据都有一定的差别，这可能源于在刚度下降阶段计算步长不够细（图中蓝线出现不光滑）导致。图10中的比较结果表明，基于拉伸试验数据可以较好地模拟本文研究中橡胶隔振器的静刚度实验。这可能是由于隔振器是一个薄壁结构，在整体受压过程中，斜壁主要受弯，因此会有相当大的区域在承受拉应变。

4 振动试验

4.1 振动试验装置

试验装置如图11(a)所示。为了与振动台可靠连接，加工了几个外径为180 mm、厚16 mm的钢圆盘（见图11(b)），圆盘上开了12个孔，通过12个螺栓配上M8的弹簧垫片与振动台连接在一起。同时在圆盘上开了两个深2 mm、直径与橡胶隔振器外直径对应的槽。在圆盘中央，开了一个贯通的直径为32 mm的孔。

图11 振动试验装置与钢圆盘示意图

为了保证轴对称，采用了轴对称的质量块（可以实现级次为3 g的加载），并且在质量块中间开孔，用一根M8长螺杆穿过橡胶隔振器的上顶面，并通过螺栓固定在一起。长螺栓两端用两个螺母拧紧，中间则夹着隔振器的上表面和被隔振质量块，最上面穿过木梁的小孔（见图12）。

图12 螺栓与橡胶隔振器连接细节

为了进一步防止侧移，用一个支架和一根木梁限制住长螺杆的上部，木梁上用电钻开一个直径比8 mm稍大的孔，并用润滑油涂抹在螺杆与木梁接触处以较少摩擦，并在木梁上设置了一个加速度传感器以监测其对系统的影响。

4.2 试验过程与结果比较

由于实验条件所限，研究中采用位移激振。分两步进行：先变频激振，在同一次激振过程中，设定激振频率以一定速率变化，测定试样加速度/底座加速度的功率谱，这主要用于观察系统的固有频率大致范围，以快速找到合适的荷载；再定点扫频，每次激振都固定一个激振频率去激励，以此分析隔振器的隔振效果。

需要说明的是，研究中并没有考虑振幅对于系统响应的影响，因为在实际试验中，若一直保持较低频率下比较适中的振幅（如8 mm），则在高频时振动会非常剧烈，有可能会破坏振动设备。而如果保持高频时比较适中的振幅（如0.5 mm），则在低频时信号会变得非常微弱，导致加速度传感器测得的数据不准确。因此，只能针对每一个阶段的频率采用不同的激振振幅和加速度，以保证每个频率下的激振信号比较适中。

以下针对基于定点扫频得到的结果进行分析。

4.2.1 定点扫频的结果

制作了10个橡胶隔振器，并对其进行了振动实验。其中，定点扫频的结果如表5所示。

4.2.2 不同壁厚的比较

对于相同倾角（为23°）和底部直径（为66 mm)的隔振器，随着壁厚从1.16 mm上升到3.27 mm，其最佳质量逐渐增加，固有频率逐渐减小，其中3.27 mm有低至8 Hz的固有频率。但当壁厚增加到5.31 mm时，由于隔振器尺寸和试验装置上方空间有限（木梁的限制），只能加载到4 kg，未使隔振器刚度达到较小值，因此固有频率较大，隔振效果不好。

4.2.3 不同底直径的比较

对比表5中壁厚为3.27 mm、倾角为23°的不同底直径隔振器的结果，以及壁厚为1.87 mm、倾角为23°、底直径为86 mm与106 mm隔振器的结果，可以看出，随着直径增大，最佳质量下降，而固有频率随之下降。至于直径86 mm时的固有频率和66 mm时一样，本文分析认为，这是由于最优质量区间比较窄，激振幅值稍微超过使系统稳定的位移值就会导致失稳，因此该质量对应的工况还不算最优。在底直径为106 mm、壁厚为3.27 mm、倾角为23°的隔振器中出现了固有频率低于3 Hz的情况，但由于要求振幅非常小，故并不稳定。

4.2.4 不同倾角的比较

对比相同的底直径和厚度工况下不同倾角（23°和30°）隔振器的试验结果，可以发现，随着倾角的增大，最佳质量增加的幅度大于固有频率增加的幅度。例如，对于底直径为86 mm、壁厚为3.27 mm的隔振器，倾角从23°变为30°时，最佳质量（即承载力）提高了67%，而固有频率仅提高2%。

在以上试验中，为使隔振器达到较低固有频率和较好的隔振效果，都必须加荷载至接近失稳状态。

5 刚度补偿的影响

在第4小节中，各隔振器都存在容易失稳的问题，因为单个橡胶隔振器作为薄壁结构，在位移到达一定值时就会失稳，但位移较小固有频率又难以降低，因此必须利用刚度补偿。本文选择了底直径为66 mm、壁厚为3.27 mm、倾角为23°的隔振器对金属小压簧进行刚度补偿。补偿系统设置了两级弹簧，较高的弹簧刚度较小，较低的弹簧刚度较大，以保证接触过程中刚度平缓过渡，如图13所示。

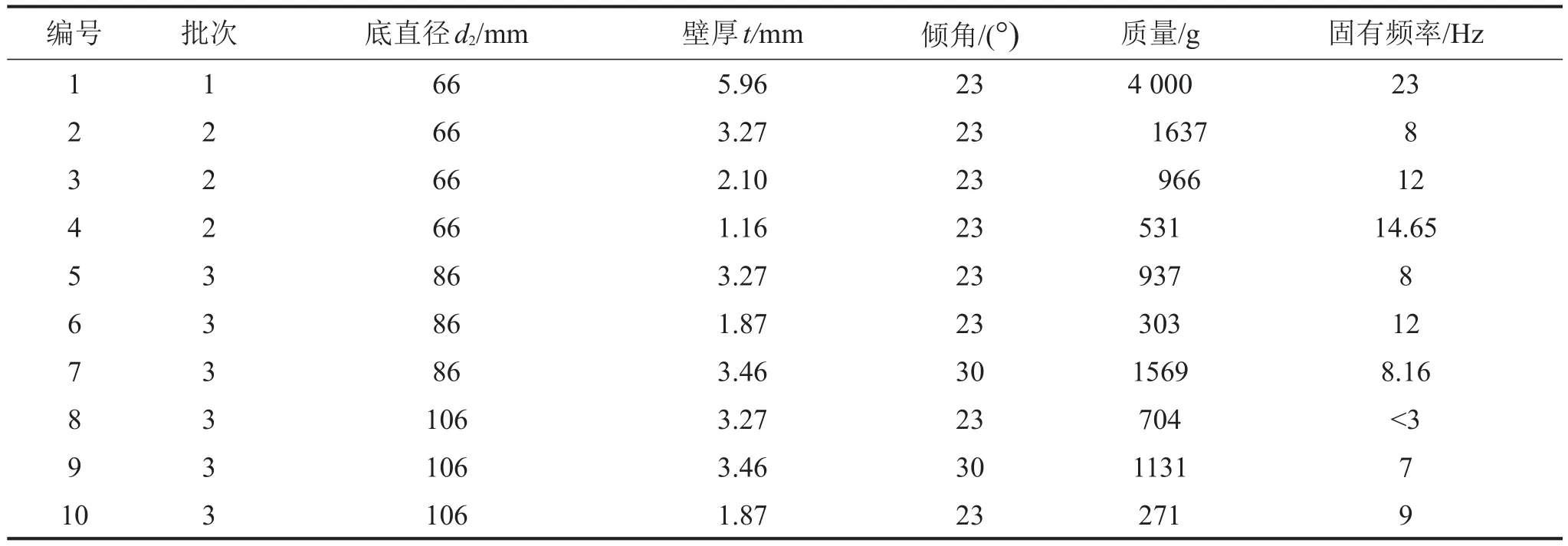
表5 单个隔振器定点扫频结果

图13 刚度补偿示意图

弹簧刚度是根据生产厂家提供了经验公式估算得到。补偿前后隔振器固有频率和传递率的变化如表6和图14所示。

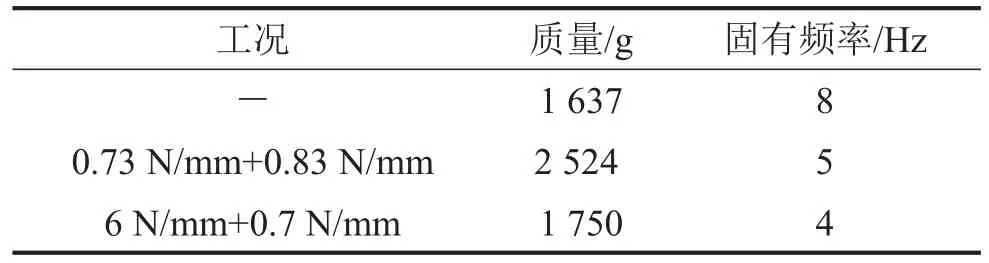
表6 补偿前后固有频率的变化

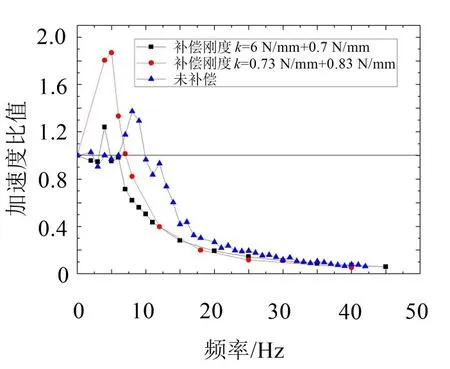
图14 补偿前后传递率曲线的变化

由表6及图14可以看出，通过适当补偿刚度，可以将固有频率降低近50%，在5 Hz～15 Hz之间，有补偿的系统传递率远小于无补偿系统；且与单个隔振器相比，在振动过程中不用担心失稳的问题。同时，所有工况下传递率峰值都不超过2，体现了橡胶隔振器较高的阻尼特性。

6 附加约束的影响

在本文的振动实验过程中，为了尽量模拟单自由度系统，采用长螺栓，施加了横梁的约束。为观察附加约束的影响，用加速度传感器记录了横梁约束影响的大小。现以底直径为66 mm、壁厚为3.27 mm、倾角为23°隔振器进行刚度补偿时的数据为例进行说明，补偿弹簧的参数分别为：1.2（线径）×18（直径）×30（高度）（k=0.73 N/mm）和1（线径）×14（直径）×20（高度）（k=0.83 N/mm）。画出每一个激振频率下每一条时程曲线中横梁加速度最大值与底座加速度值的比较（相当于木梁的传递率），如图15所示。

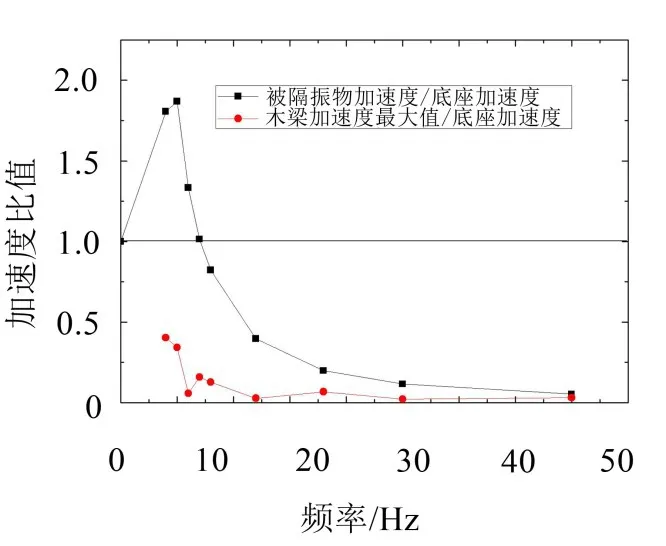
图15 附加约束干扰的大小

由图15可知，在较宽频率范围内（2 Hz～20 Hz）木梁加速度最大值与被隔振物、底座加速度相比是可以忽略的。虽然在高频区，木梁加速度最大值与被隔振物相差无几，但系统的特性在低频区已有较完全的体现（因为固有频率较低），因此可以判断在高频区系统的隔振效果也应是比较好的，所以该频率范围内干扰较大也无关紧要。

7 结语

本文采用试验与数值模拟相结合的方法对采用橡胶材料制作的一类准零刚度隔振器的刚度特性与隔振性能展开研究。通过研究得出以下结论：

(1)单个橡胶隔振器在力-位移曲线最大值附近可保持较小的刚度；

(2)通过弹簧刚度补偿的方法可以有效拓宽低刚度范围，降低最小刚度绝对值；

(3)对于主要承受压弯荷载的薄壁型橡胶隔振器，基于橡胶单轴拉伸数据进行隔振器静刚度有限元模拟具有较好的准确性。

(4)以单个橡胶隔振器作为隔振元件时，在相同条件下适当增大隔振器的壁厚可以在提高承载力的同时降低固有频率，适当增大底直径会降低承载力并降低固有频率，适当增大倾角可以在小幅增大固有频率的同时大幅增大承载力；

(5)与无刚度补偿的情况相比，刚度补偿后系统固有频率可以降低50%，并且可以解决单个隔振器容易失稳的问题；在本文设计的带补偿弹簧的隔振器中，底直径为66 mm、壁厚为3.27 mm、倾角为23°的隔振器，补偿弹簧取为6 N/mm+0.7 N/mm时，其固有频率可降至4 Hz，且系统的传递率远小于无补偿系统。同时，所有工况下传递率峰值都不超过2，体现了橡胶隔振器较高的阻尼特性。

本文在研究过程中还发现了一些问题，有待今后进一步研究：

(1)在激振过程中激振幅值对于系统响应影响的问题：在非线性理论中，系统的响应与激振频率和幅值是息息相关的，但本文在试验过程中由于实验条件所限，只能在不同的激励频率下采用不同的激振幅值，因此未能在频响曲线中发现明显的跳跃现象或倾斜的脊骨曲线等非线性系统的特征；这有待于进一步从非线性系统的角度出发进行研究；

(2)试件制作与试验时间之间的时效问题：本文第1小节中指出，橡胶性能与时间关系密切，放置时间越久弹性模量越大，但在本文振动试验中未专门针对同一个模型在不同时间的振动响应进行比较，即未充分考虑橡胶蠕变对系统隔振性能的影响；这有待于在进一步的研究中考虑。

参考文献：

[1]倪振华.振动力学[M].西安：西安交通大学出版社，1989.

[2]ALABUZHEV P,GRITCHIN A,KIM L,et al.Vibration protecting and measuring systems with quasi-zero stiffness[M].Hemisphere publishing.New York,1989.

[3]CARRELLA A,BRENNAN M J,WATERS T P.Static analysis of a passive vibration isolator with quasi-zerostiffness characteristic[J].Journal of Sound&Vibration,2007,301(3-5):678-689.

[4]YANG J,XIONG Y P,XING J T.Dynamics and power flow behaviour of a nonlinear vibration isolation system with a negative stiffness mechanism[J].Journal of Sound&Vibration,2012,332(1):167-183.

[5]张月英.准零刚度隔振器的特性分析及实验研究[D].长沙：湖南大学，2013.

[6]王毅.滚球型准零刚度隔振器的设计和特性分析[D].长沙：湖南大学，2015.

[7]余奇平.准零刚度的非线性磁力隔振器的设计和特性分析[D].长沙：湖南大学，2012.

[8]成传望.新型准零刚度隔振器的设计和特性分析[D].长沙：湖南大学，2015.

[9]周杰.碟形橡胶准零隔振器的设计与特性分析[D].长沙：湖南大学，2015.

[10]VALEEV A,ZOTOV A,TASHBULATOV R.Compact low frequency vibration isolator with quasi-zero-stiffness[C]//International Conference on Vibration Engineering,2015:1-1.

[11]VALEEV A,ALEXEY Z,ARTEM T.Study of application of vibration isolators with quasi-zero stiffness for reducing dynamics loads on the foundation[J].Procedia Engineering,2017,176:137-143.

[12]SUN X,JING X,XU J,et al.Vibration isolation via a scissor-like structured platform[J].Journal of Sound&Vibration,2014,333(9):2404-2420.

[13]CARRELLAA,BRENNAN M J,WATERS T P,et al.On the design of a high-static-low-dynamic stiffness isolator using linear mechanical springs and magnets[J].Journal of Sound&Vibration,2008,315(3):712-720.

[14]国家标准局.GB/T528-2009硫化橡胶或热塑性橡胶拉伸应力应变性能的测定[S].中国标准出版社，2009.

[15]国家标准局.GB 7757-2009硫化橡胶或热塑性橡胶压缩应力应变性能的测定[S].中国标准出版社，2009.

[16]王锐.橡胶隔振器动力学性能及设计方法研究[D].武汉：华中科技大学，2007.