金属橡胶组合刚度试验研究及仿真分析

邹龙庆，叶剑彬，付海龙，王 玥

（东北石油大学 机械科学与工程学院,黑龙江 大庆市 163000）

金属橡胶是近年来应用比较广泛的新型弹性多孔结构材料，它具有很多优点，但单一的金属橡胶隔振器刚度线性度较差，在应用于载荷幅度较大的减振对象时往往不能满足隔振要求，而组合金属橡胶可以解决这一问题[1]。2005年，李中郢、卢正人将刚度特性不同的金属橡胶元件加以组合匹配，用能量法对建模的非线性方程进行线性化，并且利用总体最小二乘法对此类方程进行参数辨识，结果表明不同的金属橡胶减振阻尼元件的互相组合将大大增加其刚度特性的线性范围[2]。2014年，李玉龙、白鸿柏等学者提出了用两块金属橡胶叠加制备隔振器的方法，解决了单个件由于具有非对称弹性力而引起隔振器拉压性能不一致的问题[3]。但在对金属橡胶组合刚度的影响因素方面的分析研究较少，所以本文对制成的单个金属橡胶试件进行组合匹配，以获得刚度特性线性区域增大的组合型隔振阻尼构件，并分析金属丝直径和金属橡胶相对密度对金属橡胶组合刚度的影响。

1 金属橡胶刚度特性

1.1 金属橡胶微元刚度分析

由金属橡胶的成型工艺可知，金属橡胶是由很多金属丝螺旋卷构成，从微观上可以将螺旋卷简化成串联和并联的微元弹簧，如图1所示。

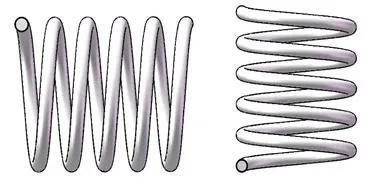
图1 微元弹簧

由金属橡胶的受力分析可知，金属橡胶所承受的力分布在这些串并联的微元弹簧上，其耗能阻尼主要是由微元弹簧之间的相互摩擦滑移所产生的，从而在隔振中起到能量耗散作用。而金属橡胶构件的耗散性能和每个微元弹簧的刚度有关，即与微元弹簧的金属丝直径和中螺旋卷直经有关。

根据弹簧的压缩计算公式[4]，可以得到单个微元弹簧的刚度

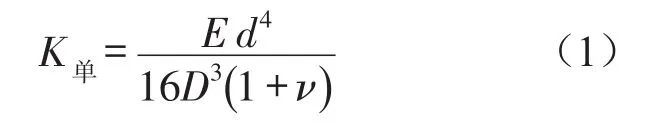
则可得微元弹簧的位移和力关系为

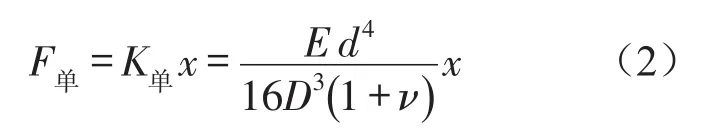
式中：F单为单个微元弹簧所受的力；K单为单个微元弹簧的刚度；d为金属丝直径；D为螺旋卷中径；E为剪切模量；ν为泊松比。

对于1个金属橡胶构件，可假设单位面积上有n个这样的微元弹簧，在单位长度方向上有m层弹簧，对于每1层内的微元弹簧，其关系为相互并联，则每1层的总刚度为

单位长度上有m层弹簧，各层之间为串联关系，则其总刚度为

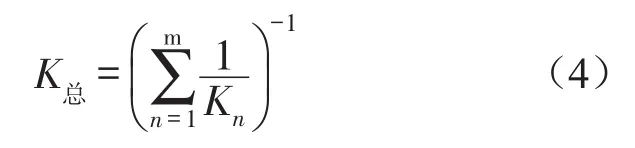
从微元角度上看，每1层微元弹簧的形态都是不相同的，假定总体上存在1个统计的平均值k，以平均值k作为单个微元弹簧的刚度，则可得

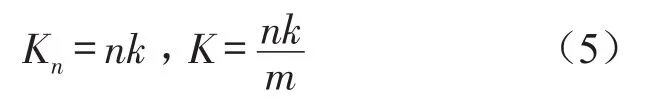
则金属橡胶的位移和载荷关系为

假设金属橡胶材料线匝在3个相互垂直方向上是等概率分布的，则单位体积的微元弹簧总数量为

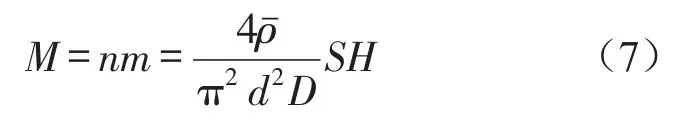
式中：为金属橡胶的相对密度；S为金属橡胶的承载面积；H为金属橡胶高度。

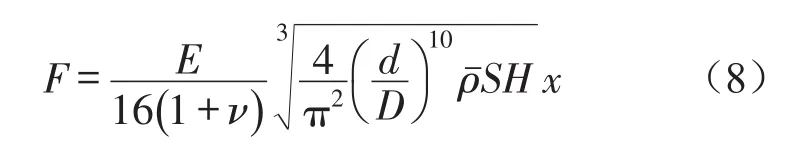
很多实验研究表明，金属橡胶的刚度呈非线性变化，所以需对式（8）进行修正，将其修正为非线性高次函数，修正后的位移-力关系为

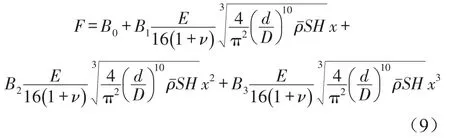
式中：B0、B1、B2、B3为修正系数，可由实验获得。

1.2 金属橡胶迟滞回线特性

在宏观上金属橡胶弹性恢复力呈现为具有记忆特性的迟滞回线[5]，这种强非线性阻尼性能一直是研究重点。Y.G.Zhou等对金属橡胶迟滞动态特性进行数学建模，研究了金属橡胶的非线性阻尼性能的机理[6]。图2所示是金属橡胶迟滞回线图，包含有加载曲线和卸载曲线。当金属橡胶成型方向受到压力时，由于金属橡胶内部的金属丝螺旋卷之间相互挤压产生滑移而产生摩擦力，能量耗散导致加载曲线和卸载曲线的不同。加载时，摩擦力阻碍变形的增加，所以使金属橡胶的实际刚度增大；而卸载时，摩擦力阻碍弹性变形的恢复，使金属橡胶实际刚度减小[7]。在图2中，加载曲线PL(X)和卸载曲线PU(X)所围成的面积为摩擦力在一个循环内所做的功。

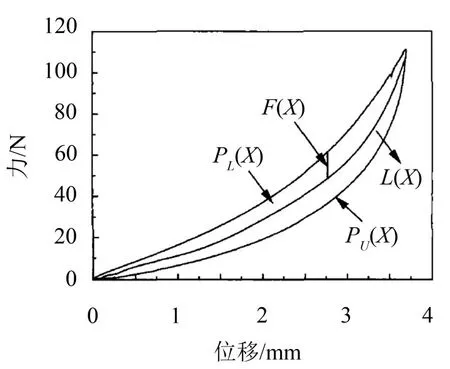
图2 金属橡胶迟滞回线

通过对金属橡胶迟滞回线的分析，可得到以下关系式

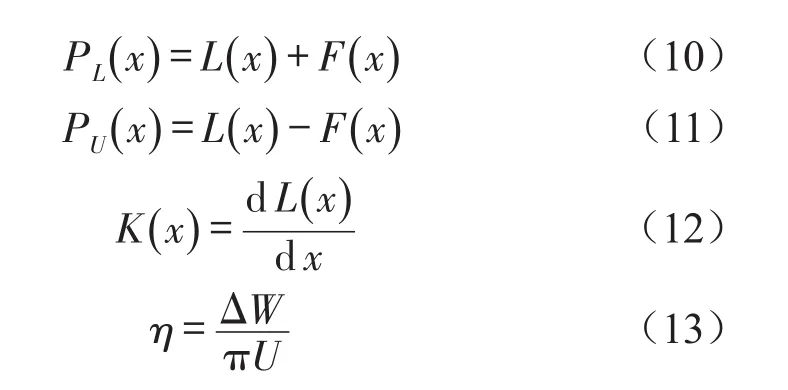
式中：PL(x)为加载力，N；PU(x)为卸载力，N；L(x)为弹性力，N；F(x)为摩擦力，N；K(x)为金属橡胶平均刚度，N/mm；η为金属橡胶耗损因子；ΔW为迟滞回线围成的面积，表示一个循环周期内所耗散的能量，N·m；U为迟滞回线中线与横轴围成的面积，表示变形过程中的最大弹性势能N·m。

根据式（10），式（11）和式（13），耗损因子的表达式为

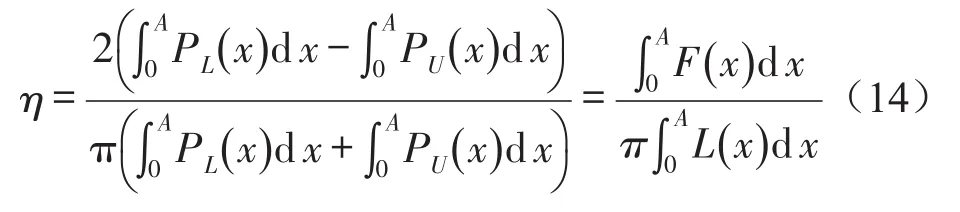
2 金属橡胶准静态试验研究

要想获得金属橡胶的刚度特性曲线及迟滞回线，需对制备的金属橡胶试件进行准静态循环加卸载试验。

2.1 金属橡胶试块的制备

以直径为0.2 mm和0.3 mm的304金属丝为原材料，利用金属橡胶自动卷簧机制备了一定质量的金属橡胶螺旋卷，并等距离拉伸螺旋卷，使其螺旋卷螺距均匀为2 mm，然后制成毛坯放在成型模具里面进行冲压成型。

所制得的部分金属橡胶试块如图3所示，试件的各项参数如表1所示。

图3 金属橡胶试块

表1 金属橡胶试块各项参数

2.2 金属橡胶准静态加载试验研究

静态试验装置使用CMT5105型100 kN全数字化微机控制电子万能试验机，该实验装置额定功率为2 kW，最大实验力为100 kN，如图4所示。

为了分析金属橡胶相对密度、金属丝不同丝径对组合型金属橡胶的影响，对所制得的金属橡胶进行组合匹配，组合方式如图5所示。

安装时尽量保证上下两块金属橡胶元件安装后压缩性能一致。A、B、C为单个金属橡胶试块，D为两个试块A的组合，E为A和B的组合，F为A和C的组合。分别对这六组金属橡胶试块进行循环加载和卸载实验，实验采用3 mm/min的加载和卸载速度近似准静态，压缩位移为2 mm。对实验数据进行处理，得到如图6所示结果。

图4 万能试验机

图5 组合型金属橡胶隔振器

由图6可得，组合型金属橡胶试件D、E和F的刚度特性明显比各自所对应的单个金属橡胶试块刚度特性大，同时，在压缩情况下，组合型金属橡胶拓宽了近似线性范围。从图6（d）中可以看出，在相对密度及螺旋卷相同的情况下，两种金属丝直径不同的组合型金属橡胶的刚度比金属丝直径相同的组合型金属橡胶要大；在金属丝直径及螺旋卷直径相同情况下，两个相对密度不同的试件相组合的刚度要比两个相对密度相同的组合型金属橡胶要大，其中相对密度的不同对其组合刚度影响较大。

2.3 理论模型与试验结果的比较

为了确定微元刚度模型中的修正系数，利用准静态压缩数据进行参数识别，利用多项式拟合确定待定系数。所用金属丝材料为304不锈钢丝，弹性模量E为210 Gpa，泊松比为0.3，金属丝的密度为7.93 kg/cm3，金属丝直径为0.2 mm，螺旋卷直径为2 mm，金属橡胶试件外形尺寸为Φ36 mm×Φ16 mm×10 mm，相对密度为0.2。采用多项式拟合，可得到方程的修正系数：B0=2.449 77，B1=6.784 48，B2=-2.688 46，B3=4.379 88。

为了验证模型的适用性和正确性，分别用表1中的B、C两组试块进行理论验证，得到的实验值和理论计算值如图7所示。

由图7可知，理论值与实验值曲线误差较小，所修正的金属橡胶微元刚度模型能较好地描述其准静态压缩过程及其与金属丝直径、螺旋卷直径、相对密度、外形尺寸的变化关系。所采用的3次多项式拟合可以较准确地描述金属橡胶的刚度特性。

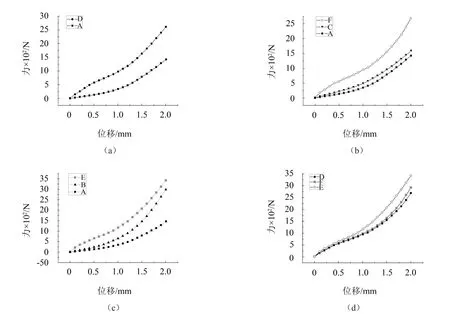
图6 组合型与单个金属橡胶试件准静态压缩实验对比

2.4 金属橡胶平均刚度

金属橡胶是用金属丝制备的纯金属材料构件，但在不同载荷作用下刚度不同。金属橡胶材料上属于各向同性，工艺上属于正交各向异性，结构上为复杂的非线性，研究其静刚度，可得出其准确的支撑能力，同时为研究动刚度提供一定参考。摩擦力在加载和卸载的过程中始终起到减小变形速率的作用，根据式（12）对具有相同位移的加载和卸载力取平均值可以得到一条新的曲线，对这条曲线求导可得出金属橡胶平均刚度变化规律[8]。利用origin软件分别对得到的新曲线进行多项式拟合，采用4次多项式进行数据拟合，拟合度R2达到0.996 91（越接近1拟合度越高），得到了如下多项式。

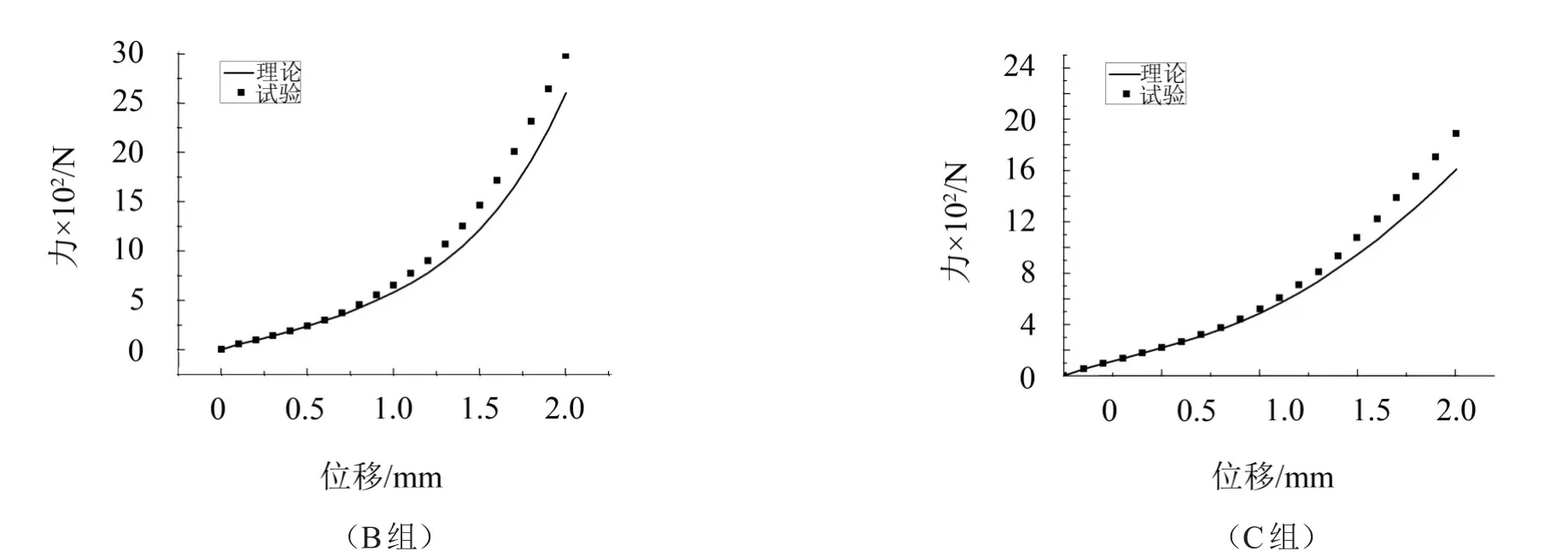
图7 理论计算值与实验值对比

分别对这6组多项式求导可得金属橡胶的平均刚度，根据多项式函数方程可得组合型和单个金属橡胶的平均刚度特性曲线，如图8所示。

从图8可以看出，组合型金属橡胶的平均刚度明显比未组合的平均刚度要大。在一定范围内，金属橡胶平均刚度表现出平稳变化趋势。同时可以看出，金属丝直径相同的情况下，相对密度高的金属橡胶平均刚度要比相对密度低的要高。

3 金属橡胶准静态压缩有限元模拟

基于金属橡胶悬臂梁杆系模型，利用ANSYS workbench有限元分析软件对组合型及单个金属橡胶试件的准静态压缩过程进行仿真分析。

3.1 悬臂梁模型

图9所示为金属橡胶悬臂梁杆系模型，假设金属橡胶试件高度为H，截面积为S，金属丝直径为d，螺旋卷直径为D，初始相对密度ρ0。取边长为D的正方体为一个微元体，则可将金属橡胶看成许多个微元体通过串、并联构成的，共n=H/D层且每层有S/D2个微元体。

由于试件实际变形过程中，其内部线匝的相互作用状态和作用数量无法观测，所以假定最大变形时所有线匝都参与接触滑移，由此确定每组悬臂梁的个数为空载时单元体内所包含的线匝数[9]

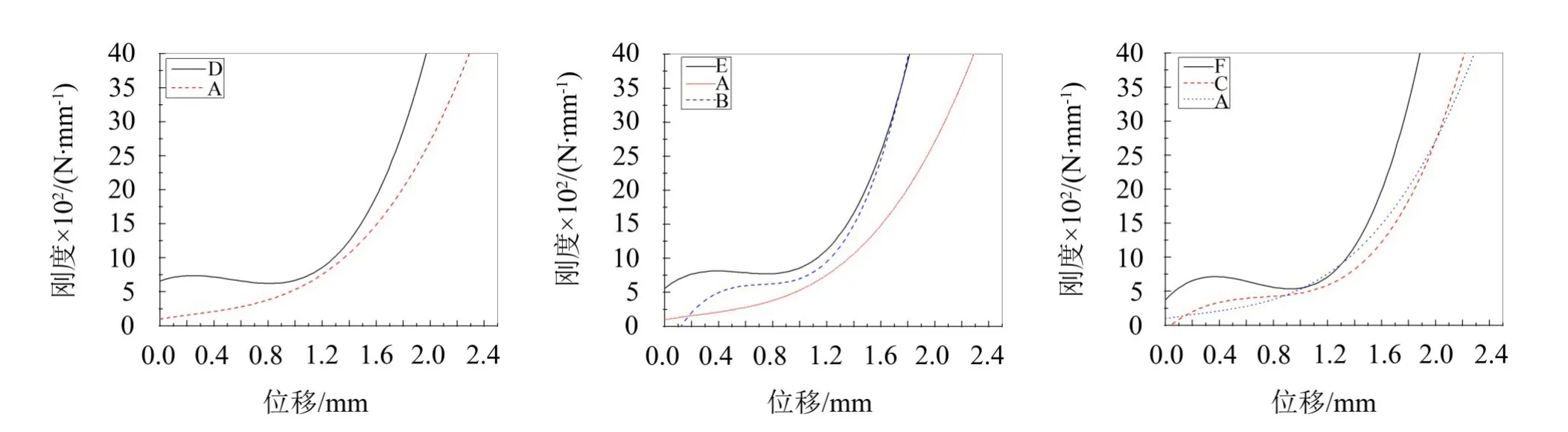
图8 金属橡胶平均刚度曲线

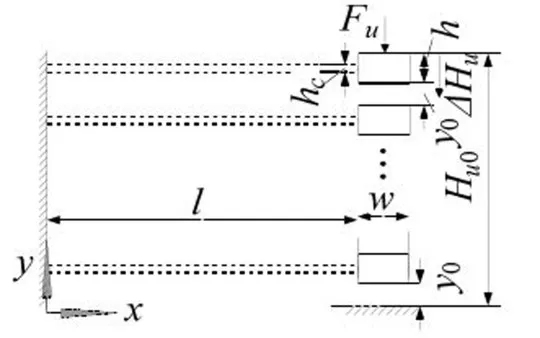
图9 金属橡胶悬臂梁模型

试件的压缩过程可表示成试件从相对密度ρ从ρ0到ρ1的变化过程，每个单元体包含有nu个方块模型，w为块体的宽，h为块体的高，h0为块体之间的间隙。当试件从ρ0变化ρ1，悬臂梁正好从第1个块体向下运动，直至与最后一个块体接触。杆长及截面尺寸决定刚度大小，取宽度与块体相同，杆长为πd的薄板，可结合试验调整，以到达较好的模拟、预测效果。可得到模型之间的尺寸关系为

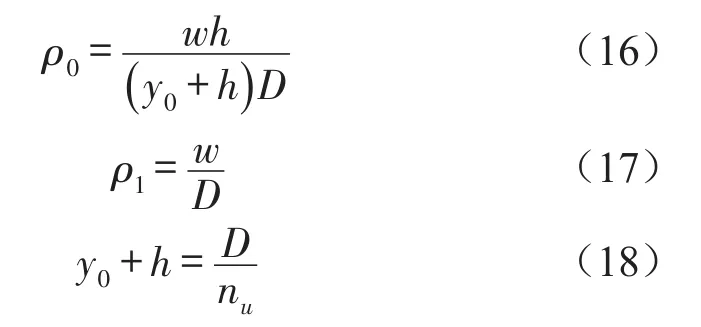
3.2 有限元模型及边界条件的设定

根据以上所分析的悬臂梁模型，对A组、B组和C组金属橡胶进行仿真分析，由式（15）至式（18）可确定悬臂梁的外型尺寸，根据相关计算，当金属橡胶压缩2 mm时，此时金属橡胶的相对密度为0.26，所以ρ1取0.26，计算结果如表2所示。

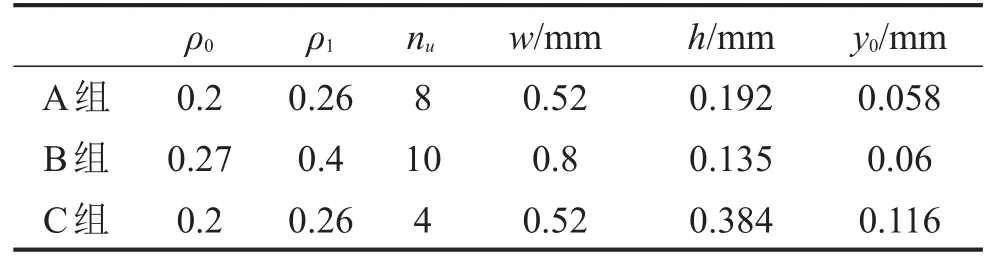
表2 悬臂梁模型尺寸参数

利用Solid Works软件对悬臂梁模型进行建模，为了区分单个和组合型金属橡胶悬臂梁模型，建立组合型金属橡胶悬臂梁模型如图11所示。

图10 A组单个型金属橡胶悬臂梁模型

将Solid Works悬臂梁模型导入ANSYS workbench有限元分析软件中，利用Transient Structural瞬态分析模块对其进行有限元分析[10]。模型材料选为304不锈钢丝的材料属性，密度为7.93 g/cm3，弹性模量为210 GPa，泊松比为0.3。在相邻两个线匝块之间建立面面接触对，选择非对称接触方式，提高计算效率，摩擦系数设置为0.3，网格划分采用sweep法。

图11 F组组合型金属橡胶悬臂梁模型

在悬臂梁的根部截面及最后1个方块的下表面施加固定约束，在第1个方块的上表面施加一个随时间变化的位移载荷，然后进行分析计算。

3.3 仿真结果分析

仿真结果如图12和13所示，图12为A组单个金属橡胶悬臂梁模型仿真结果，图13为F组组合型金属橡胶悬臂梁模型仿真结果，从结果中可以得到：要使单个金属橡胶模型的线匝块完全接触，需要加载荷7.523 N，根据试件与分析单元之间的弹性恢复力F=mFu（式中F为实验所得的压缩力，Fu为仿真所得的力，m=S/D2）可得，实验所需的载荷为1 535.444 3 N，与实际实验结果1 420.123 N相差115.210 3，误差为8.1%。组合型悬臂梁模型的线匝块完全接触需要14.027 N，而实验结果力为13.141 7 N，误差为9.3%。

提取仿真得到的数据，经过方程式F=mFu变化，得到仿真的力-位移曲线图，将其与实验结果做对比，结果如图14所示。

从图14中可以看出，仿真结果与试验相比误差小，该金属橡胶悬臂梁模型的压缩过程的总体规律与实验结果相符，能够从仿真结果中得到试件宏观上载荷和变形的非线性变化关系；在仿真结果中，组合型的金属橡胶悬臂梁模型的刚度比相对应的单个型金属橡胶的刚度要大。

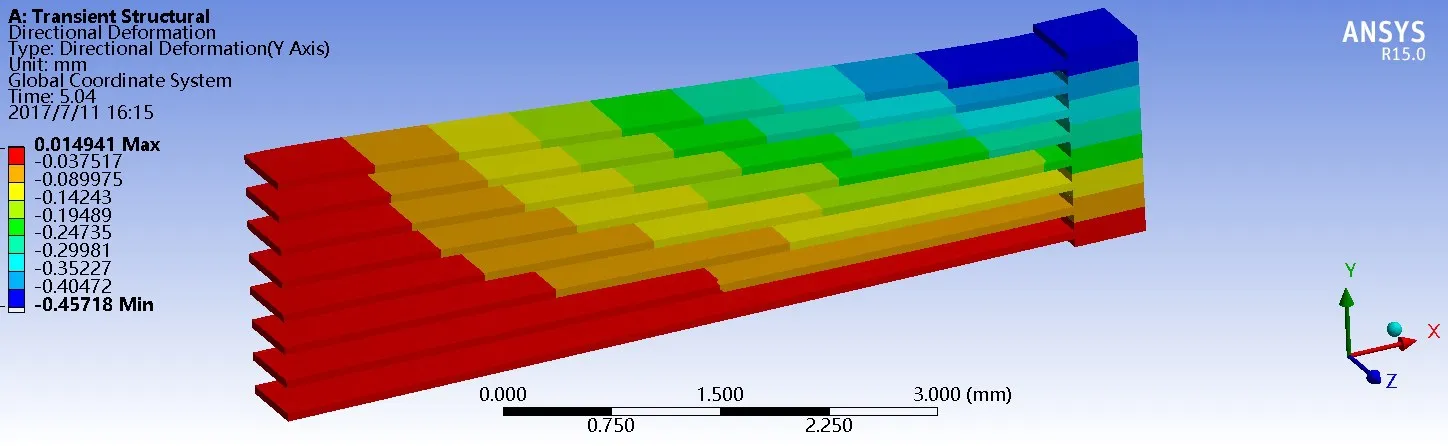
图12 A组单个金属橡胶悬臂梁模型仿真结果

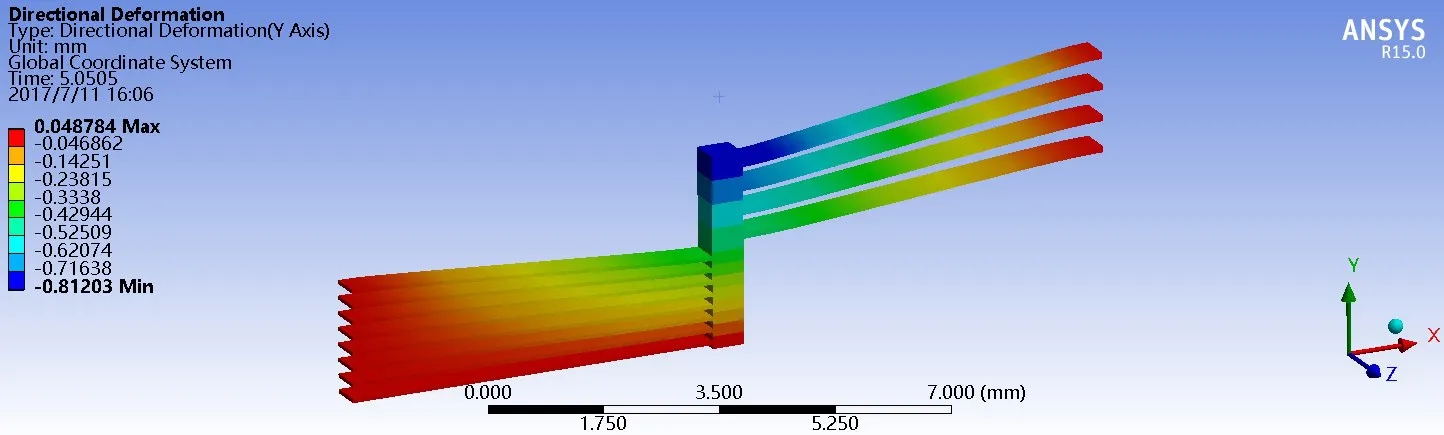
图13 F组组合型金属橡胶悬臂梁模型仿真结果

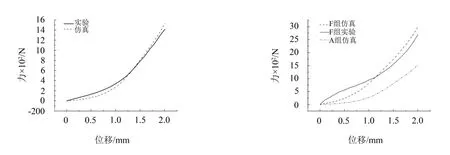
图14 仿真和实验得到的位移-力曲线对比图

4 结语

（1）本文从微观上分析了金属橡胶微元刚度，并提出了用两块金属橡胶空间叠加的组合方式组成隔振构件，对其进行了准静态加卸载试验，得到了金属橡胶的平均刚度特性曲线。从试验结果可知，组合型金属橡胶试件刚度特性要比未组合的金属橡胶试块刚度特性大，且在压缩情况下，组合型金属橡胶拓宽了刚度曲线近似线性范围；组合型金属橡胶的平均刚度也明显比单个未组合的平均刚度要大，且在一定范围内，金属橡胶平均刚度表现出平稳变化趋势。金属丝直径相同的情况下，相对密度高的金属橡胶的平均刚度要比相对密度低的高。

（2）从金属丝直径和相对密度两个方面分析了其对金属橡胶组合刚度的影响，从结果可以看出相对密度对组合刚度的影响较大。

（3）利用ANSYS workbench瞬态分析模块对单个及组合型金属橡胶基于悬臂梁杆系模型进行了有限元模拟，仿真结果误差较小，仿真效果与实验过程规律相同。

参考文献：

[1]LI ZHONG YING,LU ZHENG REN.Research on combined stiffness characteristic of metal rubber damper[J].Journal of Harbin Institute of Technology,2005,37,(10):1327-1329+1362.

[2]李中郢，卢正人.金属橡胶减振器组合刚度特性研究[J].哈尔滨工业大学学报，2005，37(10)：1327-1329.

[3]李玉龙，白鸿柏，何忠波，等.组合金属橡胶隔振系统参数识别[J].军械工程学院学报，2014(3)：68-74.

[4]张英会，刘辉航，王德成.弹簧手册[M].2版.北京：机械工业出版社，2010.

[5]MOON FRANCISC.Introductiontoexperimental nonlinear dynamics:a case study in mechanical vibration[J].Physics Today,2001,54(8):52.

[6]YAN GUO ZHOU,WEN ZHONG QU,LI XIAO.A practical mathematical model for nonlinear hysteresis of metal rubber isolator[J].Applied Mechanics and Materials,2011:20-23.

[7]朱彬，马艳红，张大义，等.金属橡胶迟滞特性本构模型研究[J]. 物理学报，2012，61(7)：474-481.

[8]崔亮，曹咏弘，关学锋.金属橡胶材料准静态加载试验及有限元模拟[J].热加工工艺，2015(20)：34-37.

[9]李明森，张文群，吴新跃.金属橡胶的悬臂梁杆系模型及有限元分析[J]. 机械，2008，35(10)：15-18.

[10]黄志新.ANSYS Workbench 16.0超级学习手册[M].北京：人民邮电出版社，2016.