金属丝网橡胶隔振器冲击加速度响应分析

刘 泽，陈 浩，王国胜，赖凌云

（中国直升机设计研究所，江西 景德镇 333001）

金属橡胶作为新型的干摩擦阻尼材料，具有承载能力强、耐高低温、抗老化及刚度可调节等优点，目前在航空隔振领域中得到广泛应用[1-3]。金属丝网橡胶材料是一种全新工艺制备的新型干摩擦隔振材料，与以往金属橡胶材料相比，在成型工艺方面进行了极大改进，传统加工方法先将金属丝制备成螺线卷，再由螺线卷缠绕制成毛坯压制成型，中间存在大量手工加工过程，难以控制环节较多[3]。金属丝网橡胶材料的加工则是先通过编网机将金属丝按规则编织成金属丝网，再对金属丝网进行纹路压制处理，最后通过模具冲压成型，机械化程度高，经实验研究发现，使用这种工艺制备的金属丝网橡胶材料隔振性能优越，力学性能更加稳定[4]。目前对金属橡胶和金属丝网橡胶的研究主要集中在其隔振动力学特性[5-6]，而在实际工程中，隔振元件经常会受到冲击载荷作用，冲击载荷所引起的响应具有极其严重的破坏性[7]，若设备的瞬时冲击响应超过了结构强度所允许的响应极限，将会导致设备损坏，严重影响设备的可靠性和使用寿命。目前对金属橡胶和金属丝网橡胶抗冲击力学性能的研究相对较少，主要以试验研究为主[7-9]，尚无对金属丝网橡胶隔振系统冲击响应的理论计算。

本文以非线性系统动力学模型为基础，结合金属丝网橡胶非线性力学特性，利用离散法推导了金属丝网橡胶隔振器冲击加速度响应计算公式，并与参考文献的试验结果进行对比分析，验证了理论的正确性并分析了误差产生的原因。

1 冲击加速度响应

图1所示为非线性系统动力学模型，其中M、F′和c′分别为系统的负载质量、非线性回复力和非线性阻尼系数，x和y分别为负载质量和隔振系统基础的位移，受到冲击脉冲时间T的加速度冲击载荷a(t)作用。

图1 非线性系统动力学模型

离散化冲击过程，将脉冲时间T进行n等分划分，每段时间间隔

则任意离散冲击时刻可以表示为

式中：m=0,1…n，tm为第m离散冲击时刻。

t0=0时刻，金属丝网橡胶的非线性弹性力与负载重力平衡，隔振系统处于静止状态。受冲击载荷后，金属丝网橡胶相对平衡位置变形量改变，产生非线性回复力和阻尼力，耗散冲击能量；且金属丝网橡胶属于干摩擦阻尼材料，其刚度和阻尼都取决于金属丝网橡胶的变形量[4]，设金属丝网橡胶相对平衡位置的变形量为s，则有

其中：F′(s)函数由金属丝网橡胶静态压缩试验确定。

由文献[3]可知，干摩擦阻尼材料具有滞回特性，加卸载一个循环内耗散的能量与总势能之比为其能量耗散系数。单独加载或卸载状态，其能量耗散系数可近似为

式中：ΔW是一个循环损耗的能量，W是一个循环总势能，由金属丝网橡胶静态压缩试验确定。

为保证隔振器具有较好的隔振性能，金属丝网橡胶一般要有20%左右的预紧量，系统阻尼比可由能量耗散系数近似替代，结合振动理论，则隔振系统非线性阻尼

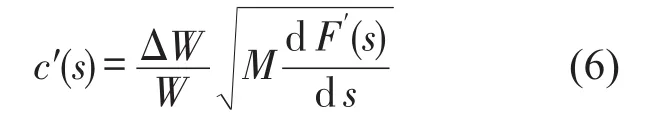
时间间隔Δt极小时，任意时刻隔振系统基础的冲击速度和位移为

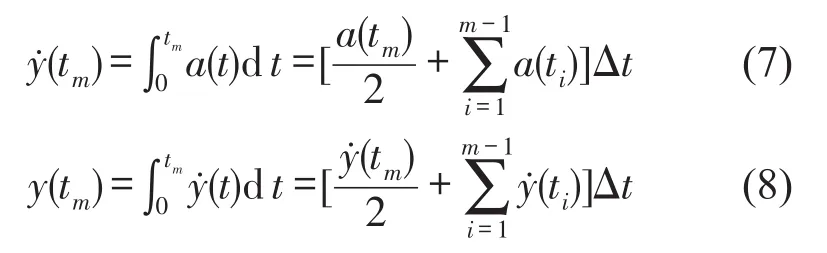
t1时刻金属丝网橡胶相对平衡位置变形量可近似为

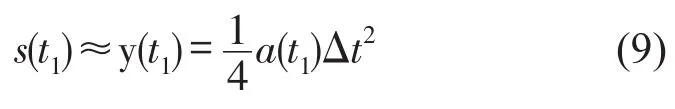
此时隔振系统冲击加速度响应

由冲击加速度响应计算冲击速度响应和位移响应为

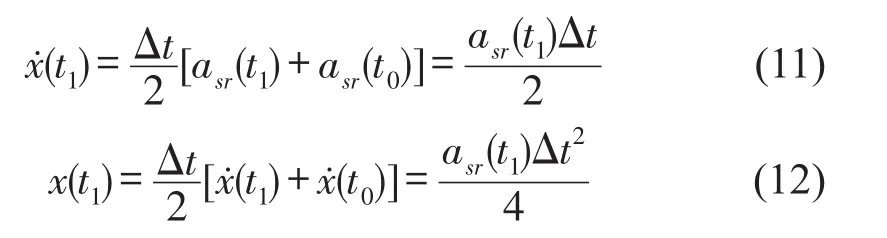
t2时刻，asr(t2)由t1时刻隔振系统非线性回复力和阻尼力近似计算为

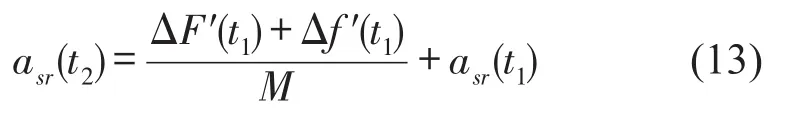
式中：ΔF′(t1)和 Δf′(t1)分别为非线性回复力和阻尼力变化量，计算公式如下

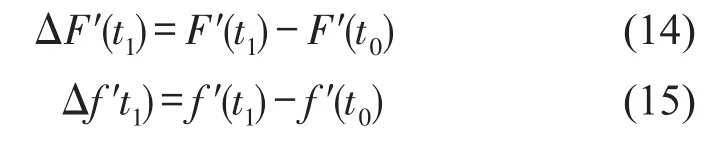
其中：非线性阻尼力f′(t0)=0 ，f′(t1)由下式计算

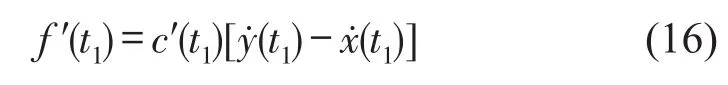
t2时刻冲击速度响应和位移响应为

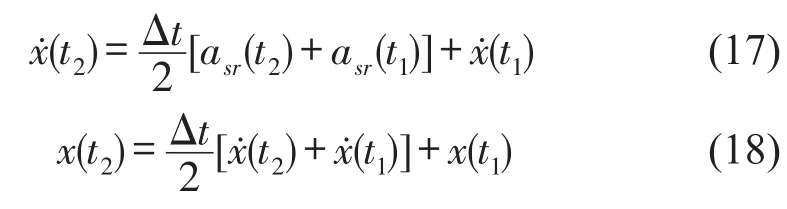
令x(t0)-y(t0)=d，由式(8)和式(12)计算t2时刻金属丝网橡胶变形量

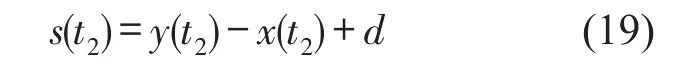
按照式(13)至式(19)计算过程依次递推，计算得到tm时刻隔振系统冲击加速度响应

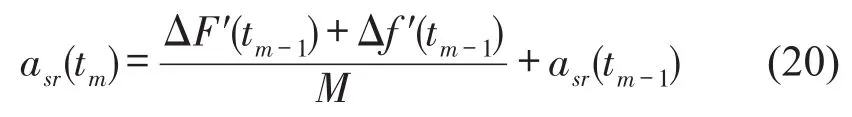
2 理论结果与试验结果对比分析

采用文献[8]的金属丝网橡胶隔振器冲击试验结果对理论进行验证，其隔振器采用两个金属丝网橡胶并联结构，受冲击载荷作用过程中，始终保持一个金属丝网橡胶试件于加载状态，另一个金属丝网橡胶试件处于卸载状态，隔振系统非线性回复力为两个金属丝网橡胶非线性回复力叠加，即

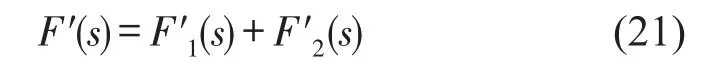
式中：F′1(s)和F′2(s)分别为两个金属丝网橡胶试件的非线性回复力。

金属丝网橡胶的预紧量为4 mm，且冲击载荷较小，金属丝网橡胶相对平衡位置变形量小于1 mm，因此，取金属丝网橡胶静态压缩力-位移曲线变形量3 mm～5 mm阶段进行叠加计算。由于静态压缩曲线卸载过程存在弹性势能损失，无法反应其非线性刚度特性，因此采用静态压缩加载曲线计算金属丝网橡胶的非线性回复力，对文献[8]中图12所示金属丝网橡胶静态压缩加载曲线进行3次多项式拟合得到其力-位移本构关系式[4]，并根据式(21)计算得到图2所示隔振系统非线性回复力曲线。

由于冲击加速度响应衰减时间长于冲击加速度脉冲时间T，因此，对冲击加速度脉冲补充0位将计算时间扩充至20 ms，计算步数n取10 000，将隔振系统非线性回复力曲线和文献[8]中表1参数代入冲击加速度响应递推计算公式，计算得到如图3所示的不同冲击高度下金属丝网橡胶隔振系统冲击加速度响应理论结果。

可以看出，理论结果与试验结果的衰减过程相同，冲击加速度响应的第1个波峰相差较小，但由于递推公式存在误差积累弊端，导致之后误差明显增大；时，金属丝网橡胶相对平衡位置的变形量最小，递推积累误差最小，从而计算误差最小；M=2.3 kg时，变形量最大，递推积累误差最大，导致计算误差最大。表1为冲击加速度响应最大值的理论值和试验值，由表可知，金属丝网橡胶的变形量相对较小时，计算精度可以控制在20%以内，相对文献[8]，对隔振系统刚度极大情况也能适用，适用范围更宽，且具有更好的计算精度。

3 结语

本文利用离散法对金属丝网橡胶隔振系统耗能缓冲机理进行研究，在非线性系统动力学模型基础上，结合金属丝网橡胶的非线性力学特性，推导了金属丝网橡胶隔振器冲击加速度响应的递推计算公式，并与试验结果进行比较，分析了误差产生的原因。研究结果表明，建立的递推计算公式能够较好地反映金属丝网橡胶隔振系统受冲击载荷后的运动规律，在金属丝网橡胶相对平衡位置变形量较小时，具有较高精度，冲击加速度响应最大值的计算误差可控制在20%以内，且公式对刚度极大情况也能够较好地反映其动力学规律，适用范围更宽。

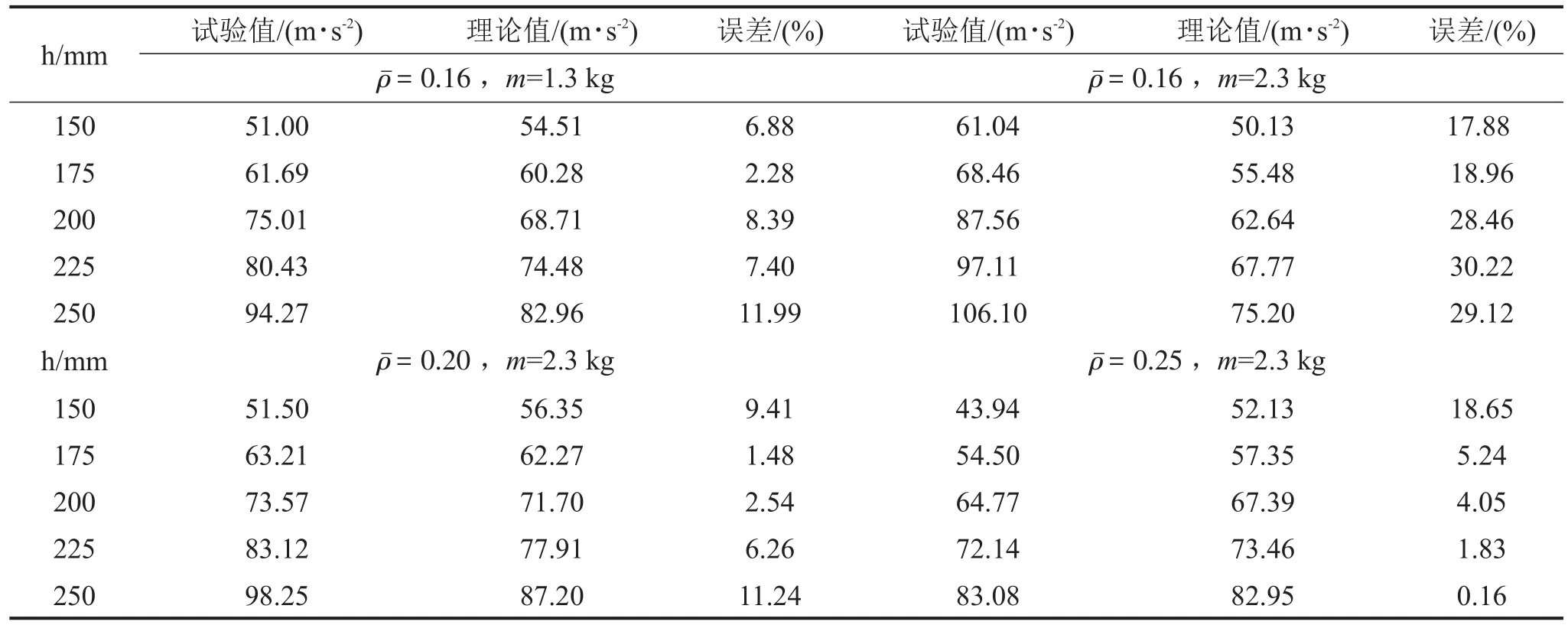
表1 冲击加速度响应最大值的理论值和试验值

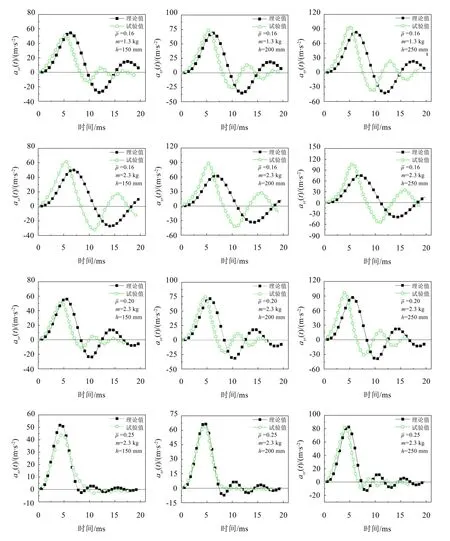
图3 冲击加速度响应理论计算结果与试验结果

参考文献：

[1]赵程，贺跃进，张恒.金属橡胶的应用研究[J].噪声与振动控制，2006，26(5)：45-47.

[2]王平，张国玉，高玉军，等.金属橡胶减振器在机载光电吊舱复合减振系统中的应用[J].振动与冲击，2014，33(5)：193-198.

[3]董秀萍，张力.新型材料金属橡胶建模及应用[M].北京：化学工业出版社，2010：5-22.

[4]邹广平，刘泽，唱忠良，等.金属丝网橡胶压缩力学性能研究[J]. 实验力学，2014，29(6)：676-682.

[5]ZHANG DAYI,MA YANHONG,HONG JIE,et al.Dynamic mechanical behavior of nickel-based superalloy metal rubber[J].Materials and Design,2014(56):69-77.

[6]MA YANHONG,LIANG ZHICHAO,WANG HONG,etal.Theoreticaland experimentalsteady-state rotordynamics of an adaptive air film damper with metal rubber[J].Journal of Sound and Vibration,2013,332:5710-5726.

[7]夏宇宏，姜洪源，魏浩东，等.金属橡胶隔振器抗冲击性能研究[J]. 振动与冲击，2009，28(1)：72-75.

[8]唱忠良，邹广平，刘泽，等.金属丝网橡胶隔振系统冲击响应[J]. 哈尔滨工程大学学报，2017，38(1)：80-85.

[9]夏金鸣，薛前光，田立强，等.金属橡胶减振器振动及冲击特性实验研究[J].可靠性与环境试验技术及评价，2012，30(2)：20-23.