GM(2,1)模型时间响应系数的优化方法

苏海军，邵 艺

（西华师范大学 数学与信息学院，四川 南充 637002）

0 引言

灰色系统理论自诞生以来，已经广泛的应用于社会、经济、管理、农业、医学等多个领域。作为其核心内容的灰色模型更是应用广泛，并取得了较好的效果。对于GM(2,1)模型，刘思峰等在文献[1]中详细给出了的定义及建模方法，并作了一定的应用。但是，原始GM(2,1)模型仍然存在着不足，主要体现在两方面：第一方面，从作为模型定义的灰微分方程跨越到求解时间响应式的白化微分方程缺乏严格理论依据，存在一定不合理性，从而导致两个方程不够匹配；第二方面，时间响应式中的两个初值是在强行指定第一个时间点和最后一个时间点的模拟值与真实值相等的条件下确定的，缺乏合理性。目前，对GM(2,1)模型的修正方法不多,文献[2]利用最小二乘法改进GM(2,1)模型算法及其预测步骤，用MATLAB实现了预测；文献[3]利用权值对一阶灰导数和背景值进行加权组合，对GM(2,1)模型进行了改进；文献[4]利用最小二乘法与数值试验的方法对GM(2,1)模型进行了改进；文献[5]提出了累积法GM(2,1)模型并对其病态性做了一定的研究,文献[6]利用微粒群算法将GM(2,1)模型拓展为 GM(2，1，λ，ρ)模型,在一定程度上提高了GM(2,1)模型的模拟精度。

本文将对时间响应式中的两个常数的确定给出较为合理的方法。在文献[1]中，GM(2,1)模型时间响应式中的两个初值是在强行指定第一个时刻点和最后一个时刻点的模拟值与真实值相等（即）条件下确定的，中间时刻点对初值的确定就没有起到任何作用，这样就造成对信息利用不够充分。理想的响应系数(c1，c2)应满足，然而这是不可能的，所以本文采用各个击破的方法，对正整数i，j(1≤i≤n-1，i＜j≤n)，寻求满足，然后利用Lingo软件再求满足最小的 (c1，c2)，通过实例验证，表明此法确定的相应系数预测精度较高。

1 基本概念

定义1[1]:设原始序列其1-AGO序列为，1-IAGO序列，其中，紧邻均值生成序列为。称：

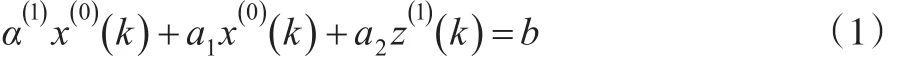
为GM（2， 1） 模型（其中k=2，3…n）；称：

为GM（2， 1）模型的白化方程。

定理1[1]:设 X(0)，X(1)，Z(1)，α(1)X(0)如定义1所述，且：

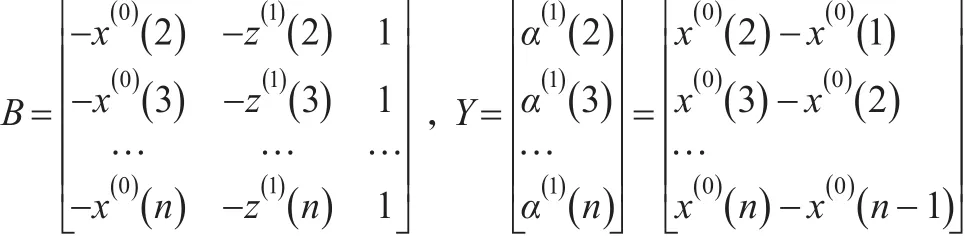
则：

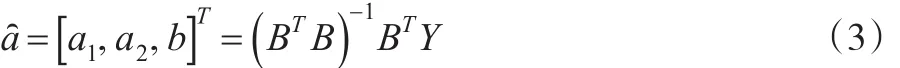
定理2[1]:关于GM(2,1)模型白化方程的解有以下结论：

结论1：设 X（1）*是方程（2）的特解，ˉ（1）是对应齐次方程的通解，则是GM(2,1)模型白化方程的通解。

当特征方程r2+a1r+a2=0有两个不相等的实根r1，r2时：

当特征方程r2+a1r+a2=0有两个相等的实根r时：

当特征方程有r2+a1r+a2=0两个共轭复根r1=α+βi，r2=α-βi时

其中，c1，c2由方程组确定。

结论3：白化方程的特解X（1）*有以下三种情况：

2 确定GM(2,1)模型时间响应式中常数c1,c2的新方法

设 X（1）*是白化方程（2）的特解ˉ（1）是对应齐次方程（4）的通解，则是模型白化方程的通解。下面分三种情形讨论：

情形1：当a1=a2=0时，0是特征方程r2+a1r+a2=0的重根，即r1=r2=0。

设 X（1）*=Bt2，代入白化方程得B=b，即 X（1）*=bt2，此时：

因此：

情形2：当 a2=0，a1≠0 时，0是特征方程 r2+a1r+a2=0的单根，不妨设r2=0，则r1=-a1。

设 X（1）*=Bt，代入白化方程得此时：

因此：

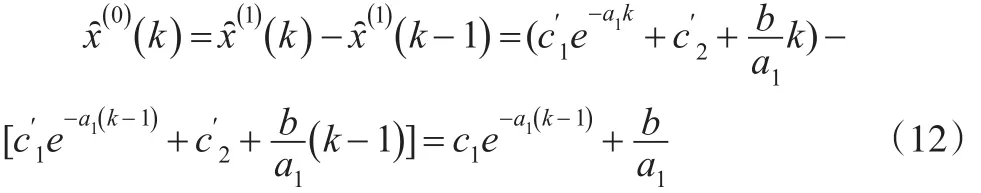
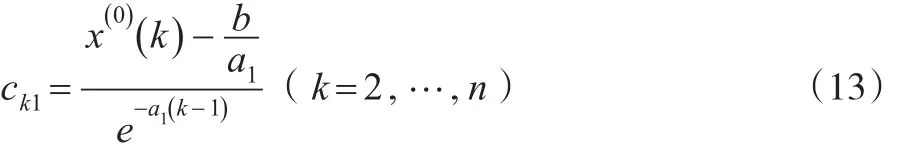
说明：此情形为DGM(2,1)模型。

情形3：当a2≠0时，0不是特征方程r2+a1r+a2=0的根，设，代入白化方程得,此时根据特征根的结果有以下三种情况。

情形1：当特征方程r2+a1r+a2=0有两个不相等的实根 r1，r2时：

因此：

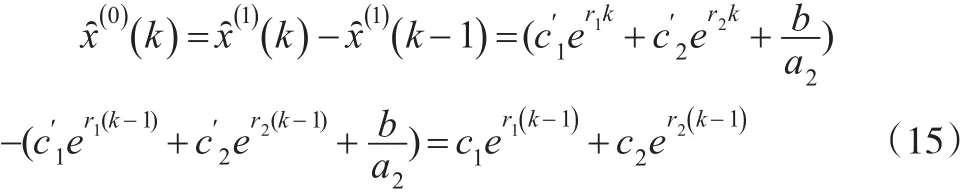
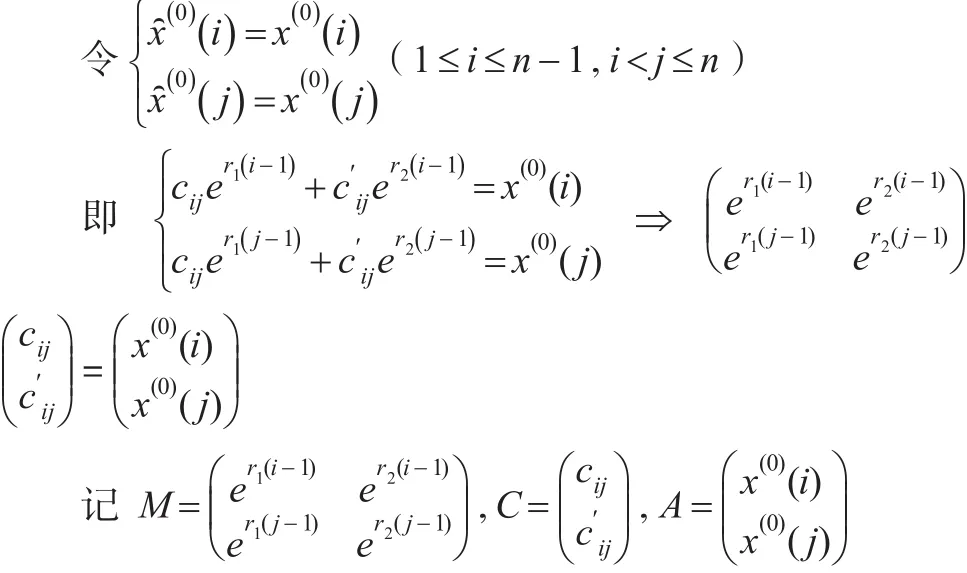
情形2：当特征方程有两个相等的实根r1=r2=r时：

因此：

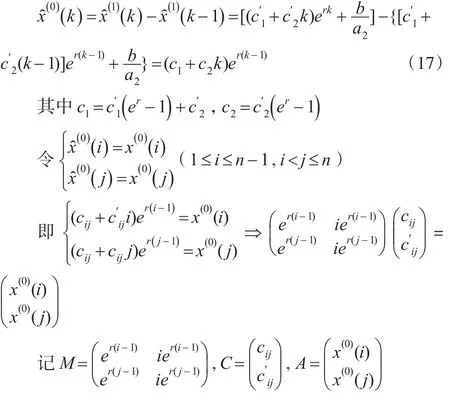
即MC=A，所以C=M-1A，由此得出再利用情形1的方法求得c1，c2。

情形3：当特征方程有两个共轭复根r1=α+βi，r2=α-βi（仅此处i为虚数单位）时：

所以：

即MC=A，所以C=M-1A，由此得出

再利用情形1的方法求得c1，c2。

3 模型应用与比较分析

以文献[1]第174页的数据序列：X(0)=(2.874，3.278，3.337，3.39，3.679)为基础建立GM(2,1)模型。

按本文方法推导预测公式：

X(0)的1-AGO序列和1-IAGO序列分别为：

X(1)的紧邻均值生成序列为：

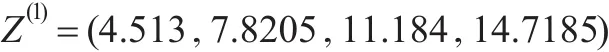
故得GM(2,1)的白化方程：

特征方程有两个不相等的实根r1=2.0215，r2=0.0428，属于本文情形3的第(1)种情况。

初始值分别为：

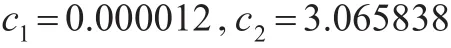
将 r1，r2,c1，c2代入（15）得：

几种预测方法的精度对比：

文献[1]GM(2,1)模型、文献[6]GM(2,1,λ,ρ)模型以及本文GM(2,1)模型的精度检验见表1（其中文献[1]、文献[6]的计算结果直接取自文献[1]、文献[6]）。由表1可以看出，按本文所提的方法进行GM(2,1)模型的计算可以得到更好的效果。

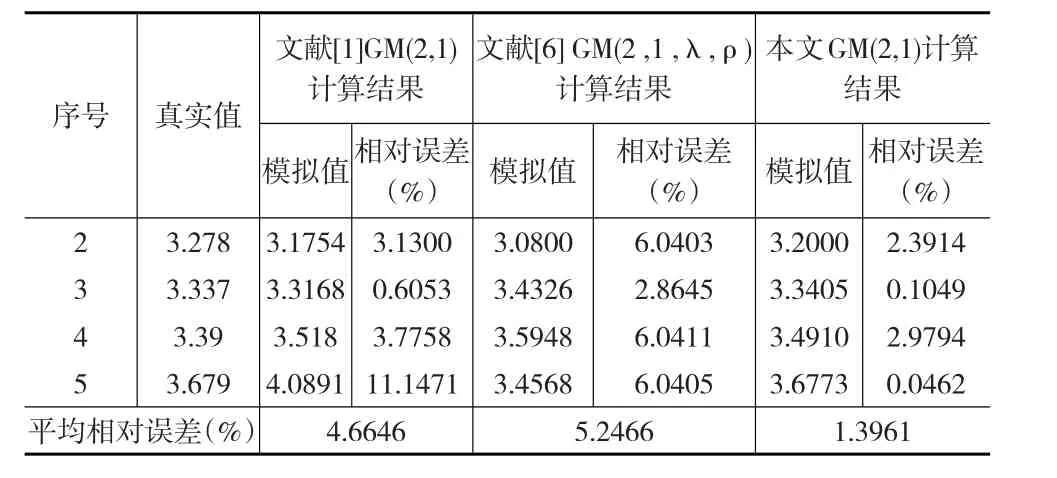
表1 精度检验

4 结束语

GM(2,1)模型白化响应式中常数c1，c2的确定直接影响模型的精度，原始GM(2,1)模型的时间响应式中两个初值是在强行指定第一个时刻点和最后一个时刻点的模拟值与真实值相等的条件下确定的，中间时刻点对初值的确定没有起到任何作用，造成了对信息利用不够充分；理想的响应系数 (c1，c2)应满足这显然是不可能的，因此本文退而求其次，各个击破，对正整 数 i，j（ 1≤i≤n-1，i＜j≤n ），寻 求满足，然后利用Lingo软件再求满足最小的，通过实例验证，表明此法确定的相应系数预测精度较高。

参考文献：

[1]刘思峰，党耀国，方志耕，谢乃明.灰色系统理论及其应用[M].北京：科学出版社，2010.

[2]李玲玲，单锐，崔红芳.改进GM(2,1)模型的MATLAB实现及其应用[J].数学的实践与认识,2011,41(20).

[3]牛思先，陈鹏宇，苏玉刚.基于加权组合最小二乘法改进的GM(2,1)模型[J].统计与决策,2010,(22).

[4]沈继红,赵希人.利用最小二乘法改进GM(2，1)模型[J].哈尔滨工程大学学报，2001,22(4).

[5]曾祥艳,肖新平.累积法GM(2,1)模型及其病态性研究[J].系统工程与电子技术,2006,28(4).

[6]刘虹,张歧山.基于微粒群算法的GM(2，1，λ，ρ)优化模型[J].系统工程理论与实践,2008,10(10).