基于核主成分分析和粒子群优化支持向量机的统计数据缺失值插补

吴桐雨，吴少雄

（1.福州大学 经济与管理学院，福州 350116；2.福建工程学院 交通学院，福州 350118）

0 引言

现有统计数据因各种原因存在缺失值，给统计分析带来一定的困难。通常采用删除缺失的单元项进行统计分析，然而这种做法会丢失有用的信息，容易得出误导性的结论。插补技术能够为缺失项确定一个合理的数值，减小由数据缺失带来的估计偏差，完善统计数据集利于后期操作。

常用的插补方法有演绎估计、均值插补、随机插补、回归插补和多重插补、极大似然估计、EM算法等；李序颖考虑空间相关性引入空间自回归模型；张松兰提出统计方法与机器学习相结合的支持向量机、神经网络和决策树方法[1]；其他方法还有最近邻插补法和关联规则法、得分匹配法等。其中，单值插补的不足在于根本上改变了数据的原始分布，造成抽样误差，且不能很好地体现出缺失值的不确定性。空间自回归模型需要验证数据间的相关性，对相邻缺失值的插补可能存在一定的偏差，难以处理大量的缺失数据。研究表明，通过学习相关度较大的已知属性值进行估计的精度更高[1]，用支持向量机方法对数据进行插补较传统方法有更高的恢复率[2]。总的说来，采取以上方法处理数据缺失存在各自的优势，但也有其不足之处，比如一些研究仅适用于小样本情况下的插补，对于大样本插补的精度有所下降；一些研究虽然考虑了数据间的影响关系，但考虑的因素并不全面；大部分文献集中于研究社会调查中的数据缺失插补方法，鲜有文献研究统计数据的缺失插补方法，而且插补的精度还有待进一步改善。支持向量机作为一种新兴的统计学习算法在模式识别、回归估计等方面均取得理想效果，本文以福建省流通产业的统计数据为例，将核主成分分析、粒子群算法和支持向量机三者有机结合，对统计数据的缺失值进行插补。

1 模型原理

1.1 核主成分分析（KPCA）

核主成分分析是通过一个非线性变换将数据从输入空间投影到高维特征空间，然后在高维空间进行线性主成分分析，其中，非线性变换通过定义内积函数实现，该函数由一个核函数代替。这种方法可以避免单纯使用线性主成分分析遇到的特征向量线性不可分的问题[3]。

根据 λν=Cν，求C的特征值 λ及特征向量V∈F{0}，C的特征值非负。设C的特征值为0≤λ1≤λ2≤…≤λn，对应的特征向量为 ν1，ν2，…，νn。记：

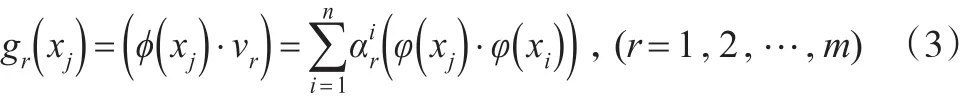
在实际操作中，可以根据一定的规则选取式（4）的前几个分量作为主成分。

1.2 粒子群优化（PSO）

粒子群优化是一种智能群体搜索方法，其基本思想是初始化为一群随机粒子，每个粒子代表解空间的一个候选解，粒子通过跟踪个体最优值和全局最优值来更新自己的速度和位置，迭代直至达到预先设定的目标则实现最优解[4]。粒子通过以下两个公式更新其位置和速度：

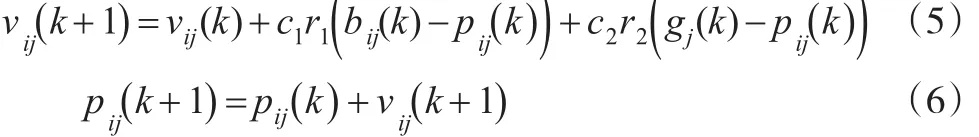
式中，k为进化代数，νij（k+1）为粒子i在第k次迭代中第j维的速度，νij∈[ ]-νmax，νmax，νmax是粒子被允许移动的最高速度；c1，c2是加速系数，通常取值为2；r1，r2是[0,1]之间的随机数；pij是粒子i在第j维上的个体极值点的位置，pij∈[ ]-pmax，pmax，pmax是粒子被允许移动的最大位置；gj是整体在第j维上的全局极值点的位置。设搜索空间的第j维定义为区间 j∈[ ]-pjmax，pjmax，则通常有

1.3 最小二乘支持向量机

最小二乘支持向量机的基本思想是通过非线性变换将数据映射到高维特征空间，并构造最优决策函数，利用原空间的核函数代替高维特征空间中的点积运算，用有限样本的学习训练来获得全局最优解[5]。

对于给定的样本数据，作非线性映射Φ:Rn→F，则被估计函数 f(x)为：

在权w空间中的函数估计描述为以下求解问题：

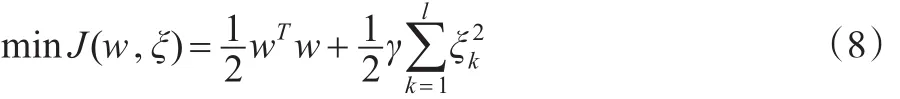
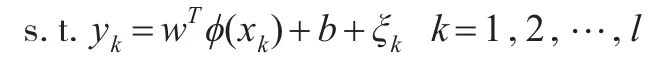
其中：w为空间F中的权向量，b∈R为偏置，误差变量ξk∈R,b是偏差量，γ是可调超参数。

根据式（8），可定义拉格朗日函数：

其中，拉格朗日乘子ak∈R。对上式各变量求偏导并整理线性方程组：

最小二乘支持向量机的函数估计为：

其中，a、b由式（9）求解出。不为零的ai对应的样本为支持向量。

2 流通产业统计评价指标与数据

在研究省域流通产业评价指标体系中，将评价指标分为6个一级指标，22个二级指标，45个三级指标[6]，具体见表1。

表1 省域流通产业竞争力评价指标体系

由于我国对流通产业的统计并没有统一的口径，而是分散在批发业、零售业、餐饮业、交通运输、仓储和邮政业几个行业中。本文共收集了各省从1949—2015年85项统计指标的数据，数据来源于《中国统计年鉴》、《中国贸易外经统计年鉴》、《中国第三产业统计年鉴》等。其中，1949—1991年和2015年统计数据缺失较多，1992—2014年存在少量缺失值，若将含有缺失数据的年份全部剔除后进行分析，将会丢失大量有用的信息，对流通产业竞争力的评价可能会出现误导性的结果。因此，选取1992—2014年含有缺失值的福建省流通产业相关统计数据为例进行数据插补研究。

3 统计数据缺失值插补

3.1 统计数据缺失值插补过程

统计数据缺失值插补的详细流程如下：

（1）为增加样本集和提高数据修补的准确性，采用增量变化的方法进行数据处理，即将各年份的数据相减所得作为训练与测试的样本，这样23年的统计数据共产生132组数据。

（2）因各项统计数据存在较大差异,且量纲不一致,需对数据进行预处理，使它们统一归一化到-1～1。

（3）选取有数据缺失的指标作为研究对象，采用高斯径向基核函数，对其余的44项统计指标进行核主成分分析。主成分累计贡献率如图1所示，其中第1主成分贡献率为0.266，第2主成分累计贡献率达0.448，第13主成分的累计贡献率为0.908，选取前13个主成分作为最小二乘支持向量机的新影响因子。

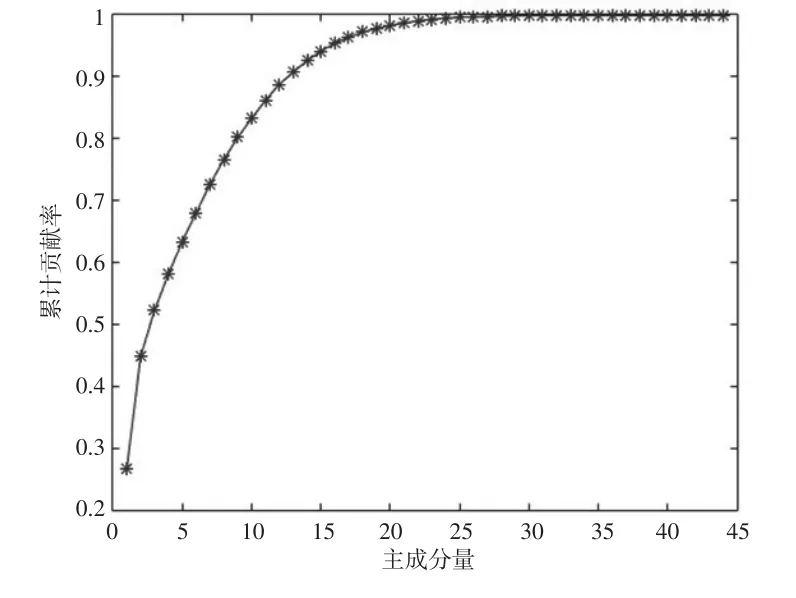
图1 主成分累积贡献率

（4）将新影响因子和数据缺失指标的数据分成两部分，前100组数据作为训练样本，后32组数据为测试样本。

（5）应用PSO优化最小二乘支持向量机的超参数，加速系数c1.c2均设为2，惯性权重w设为0.6，种群规模设为20，最大迭代步数设为100。搜索得到支持向量机的参数惩罚因子=3124.8795和RBF核函数参数=20.5206。

（6）应用最小二乘支持向量机对样本分别进行训练和测试，测试结果如图2和表2所示。

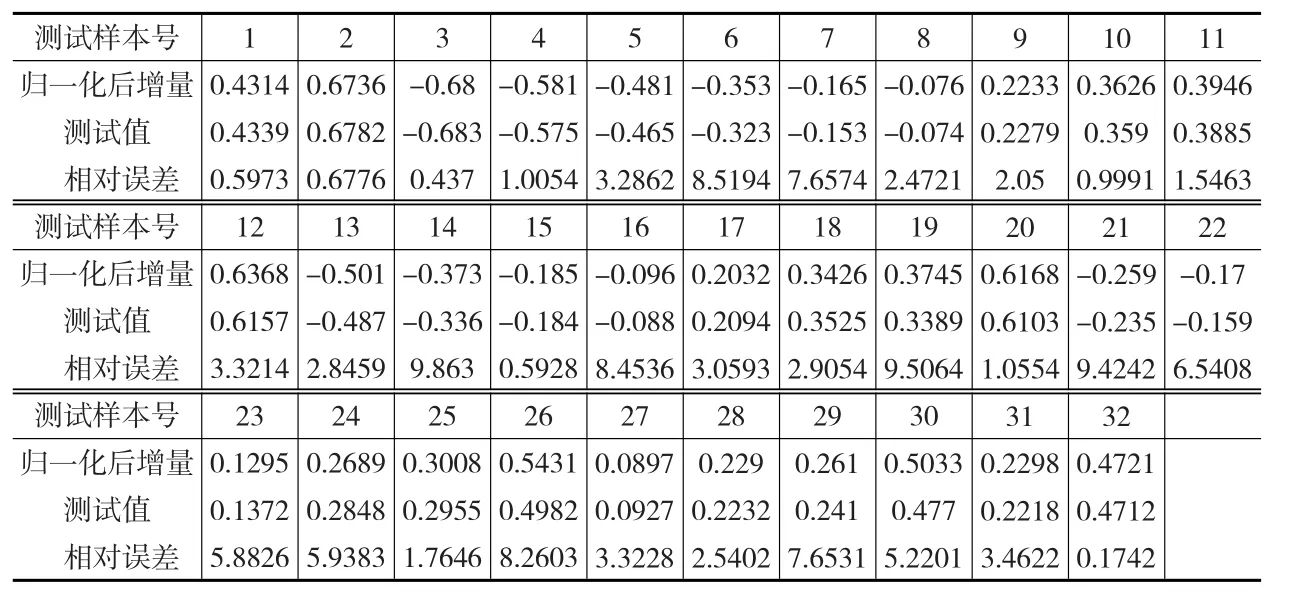
表2 测试结果分析

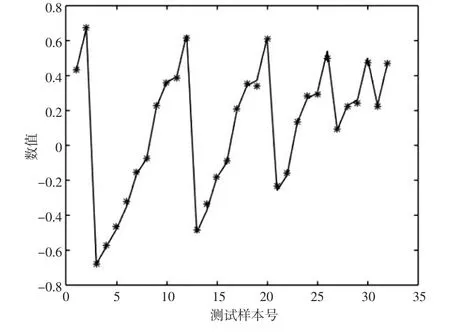
图2 模型测试值与真实值比较

3.2 测试结果分析

由表2可以看出基于核主成分与支持向量机的方法进行数据插补可以取得较好的效果，最大相对误差为9.863%，最小相对误仅为0.1742，平均相对误差为4.094%。

4 结论

在开展统计数据分析时，对缺失数据进行插补是十分必要的。将核主成分分析与支持向量机模型结合，建立数据插补模型，具有很好的非线性信息提取和降噪的能力，研究表明其具有较高的精度，可以应用于数据插补。

参考文献:

[1]张松兰,王鹏,徐子伟.基于统计相关的缺失值数据处理研究[J].统计与决策,2016，(12).

[2]张婵.一种基于支持向量机的缺失值填补算法[J].计算机应用与软件,2013,30(5).

[3]Scholkopf B,Smola A J,Muller K R.Kernel Principal Component Analysis[M].Massachustees：MIT Press,1999.

[4]杨维,李歧强.粒子群优化算法综述[J].中国工程科学,2004,6(5).

[5][美]瓦普尼克.统计学习理论的本质[M].北京：清华大学出版社,2000.

[6]张连刚.省域流通产业竞争力评价体系构建与实证研究[D].成都：西南财经大学博士学位论文,2011.