基于可能性均值-方差距离的模糊线性回归模型参数估计

龚艳冰，杨舒馨，戴靓靓

（河海大学 企业管理学院，江苏 常州 213022）

0 引言

针对现实世界语言值的模糊性，1982年名古屋大学的Tanaka等首次提出了模糊线性回归模型，主要考虑自变量为非模糊数、回归系数为对称三角模糊数的回归模型，并将参数估计问题转化为线性规划问题[1]。Diamond等在三角模糊空间上定义一个适当的距离，利用最小二乘原理得到另一种模糊回归分析模型的参数估计方法[2]。Chang等对现有模糊回归模型进行了分析比较，并总结了模糊回归分析常用的二种方法，即线性规划方法、模糊最小二乘方法[3]。模糊回归模型是模糊集理论与传统回归方法的结合，在实际应用中收到了较好的效果，之后国内外许多学者对模糊线性回归模型的参数估计方法进行了大量研究[4-8]。

本文试图利用模糊数的统计特征（可能性均值、方差），从影响模糊数的主要特征出发，利用最小二乘原理，从可能性均值-方差距离最小的角度估计模糊回归模型的参数。本文方法考虑决策中的主观模糊性，在某种程度上提升了模糊回归模型的灵活性和合理性。

1 基本概念及定义

定义1：假定模糊数A的隶属函数为：

则称A=(a，α，β)为三角模糊数，其中α，β称为三角模糊数的左右扩展。根据Zadeh的扩展原理，可得三角模糊数 A=(a，α1，β1)和 B=(b，α2，β2)的算术运算法则为[5]:

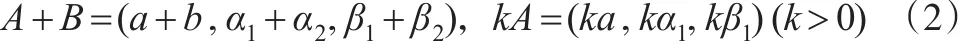
定义2：设模糊数A的 γ截集为 A(γ)=[al(γ)，au(γ)]，则模糊数A的可能性均值和方差分别为[9]：

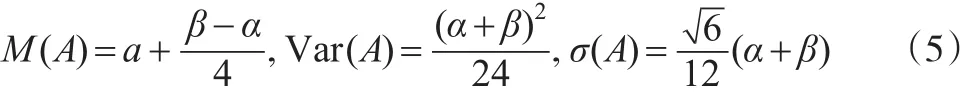
2 模糊线性回归模型参数估计

对于模糊线性回归模型的讨论，大致可以分为以下三种情形：①输入自变量为实数值，输出因变量和待估计参数为模糊数的线性回归模型，②输入自变量和输出因变量为模糊数，待估计参数为实数的线性回归模型，③输入自变量、输出因变量、待估参数均为模糊数的线性回归模型，本文主要考虑第一种情况，即：

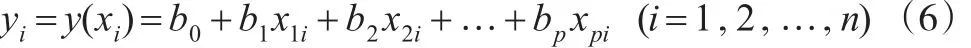
其中，xji表示实数解释变量，yi表示模糊响应变量，bj为待估计模糊回归系数，一般假定大于0。特别的，以三角模糊数为例，令三角模糊数 bj=(kj，αj，βj)(j=1，2，…，p)，则上述模糊线性回归模型（6）可改写成：

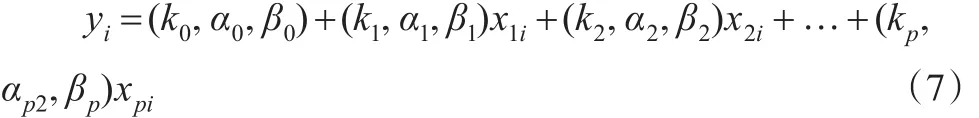
利用三角模糊数的运算法则式（2），对上述三角模糊数回归模型（7）进行线性表示：

其中 x0i=1，要确定模糊回归系数2，…，p)，通常方法是定义模糊数之间的距离，使得模糊回归问题转化为最小化模糊距离的问题，从而使得给定的模糊距离下响应变量观测值与响应变量估计值之间的误差最小，即：

上述模型（9）的最小值很难直接求出，本文在文献[18]中采用最小一乘回归方法估计模糊回归系数，但是最小一乘回归的计算相对复杂得多，相对而言，最小二乘回归的计算更为简单,效果也在整体上更好。为了估计模型（7）的参数，首先给出可能性均值-方差欧氏距离的概念，即模糊数A和B的距离可以定义为：

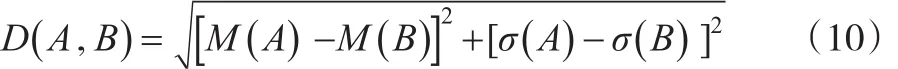
显然，三角模糊数A和B的可能性均值-方差欧氏距离满足距离测度的非负性、对称性和三角不等式性质，即：

为了估计模型（7）的自变量回归系数，可将模糊因变量估计值与观测值间的均值-方差最小二乘距离误差平方和作为模型（9）的近似估计，即：

对于三角模糊数将式（5）代入式（11），可得误差平方和为：

根据最小二乘原理，对于 j=0，1，…，p上述误差平方和最小，只需令：

记：

则等式（13）至等式（15）可以写成下列矩阵形式：

通过求解上述线性方程组（16）可得到模糊线性回归模型（7）的回归系数的估计值，这比文献[18]求解线性规划模型要简单，称这种最小二乘参数估计方法为可能性均值-方差距离最小二乘方法（Possibilistic Mean-Variance Distance Least Squares Method），简称PMVD-LSM。为了比较PMVD-LSM的估计效果，将拟合值与实际值之间的可能性均值-方差误差平方和作为误差估计的检验依据，当回归方程拟合出来的模糊回归模型具有较小的e值，则说明该模型应该是不错的模型。

3 实例

为了说明本文方法的可行性，参考Coppi等给出的一氧化碳（CO）浓度的例子进行实证研究[10]，Coppi等收集了罗马地区1992年10月份连续21天大气中一氧化碳浓度每小时检测一次的数据。研究表明，一氧化碳浓度与一些气候变量相关，一氧化碳浓度（因变量y）的六个主要影响因素（自变量）包括：温度(x1)、相对湿度(x2)、大气压强(x3)、降雨量(x4)、辐射强度(x5)、风速(x6)。这些气候变量每天检测一次，如果以天为观察单位，在计算一氧化碳浓度数据时，如果仅仅通过平均值来描述每一天的观测值，则会损失很对信息。针对这种情况，一个可行的方法就是将每天的一氧化碳浓度看出一个三角模糊数yi=(ymi，yli，yui)，其中 ymi表示第i天的CO浓度数据的均值，yli表示最小值，yui表示最大值，即三角模糊数的左右扩展，如表1所示。

表1 自变量和因变量观测值

采用Matlab统计软件，将上述样本数据代入线性方程组（16）可以计算出模糊回归参数的三角模糊数估计为：

根据式（8）计算上述回归模型的预测值yc，并按照可能性均值-方差距离公式（10）计算预测值 yci=(ycmi，ycli，ycui)与 实 际 值 yi=(ymi，yli，yui)之 间 的 误 差 平 方 和，将其作为误差估计的检验依据。

同时，为了说明本文方法的有效性，将本文方法与文献[11]的结构元方法和文献[14]的最小一乘方法进行比较，结果如表2所示。比较结果表明，本文的基于可能性均值-方差距离最小二乘估计方法与可能性均值-方差距离最小一乘估计方法误差基本一致，但是本文方法只需要计算简单的线性方程组，而文献[14]则需要计算线性规划模型，与文献[11]的基于结构元距离最小二乘方法比较，本文的可能性均值-方差距离估计参数效果更好。

4 结论

最小二乘估计方法是模糊线性回归模型中常用的参数估计方法,考虑到三角模糊数的普遍性，针对数据输入参数、输出为三角模糊数的模糊线性回归模型，引入模糊数的可能性均值和方差的概念，在此基础上，定义可能性均值-方差欧氏距离，提出了模糊线性回归模型的最小二乘参数估计方法，并对模型进行了误差分析。通过实例计算和其他模型的比较结果表明，本文的方法具有良好地拟合效果，且计算简单。

表2 拟合效果与距离误差测度表

参考文献：

[1]Tanaka H,Uejima S,Asai K.Linear Regression Analysis With Fuzzy Model[J].IEEE Transactions on Systems Man,and Cybernetics,1982，（12）.

[2]Diamond P.Fuzzy Least Squares[J].Information Science,1988,（46）.

[3]Chen L H,Hsueh C C.Fuzzy Regression Models Using the Least-squares Method Based on the Concept of Distance[J].IEEE Transactions on Fuzzy Systems,2009,（17）.

[4]Wan S P,Dong J Y.Possibility Linear Programming With Trapezoidal Fuzzy Numbers[J].Applied Mathematical Modelling,2014,（38）.

[5]柏林，房勇.基于模糊回归分析的投资组合选择模型[J].系统工程理论与实践,2015,35（7）.

[6]彭宇文,郭莉莎,毛超.基于改进模拟退火算法的模糊回归参数估计[J].统计与决策,2014，（1）.

[7]汪华东，郭嗣琮，岳立柱.基于结构元理论的模糊多元线性回归模型[J].系统工程理论与实践,2014，34（10）.

[8]岳立柱.系数为一般模糊数的多元线性回归模型[J].统计与决策,2015，（3）.

[9]C.Carlsson,R.Fullér.On Possibilistic Mean Value And Variance of Fuzzy Numbers[J].Fuzzy Sets and Systems,2001,（122）.

[10]龚艳冰,戴靓靓,胡娜.基于可能性均值-方差距离的模糊最小一乘回归模型[J].统计与决策,2017，（22）.