基于校园数据的插值法应用

付 裕

（陕西国防工业职业技术学院，西安 710300）

许多实际问题都可以用一函数f（x）来表示其内在规律的数量关系。这种函数中相当的一部分是通过试验或观测得到的。插值法是一种古老的数学方法，它来自生产实践。其核心思想就是根据给定的数据做一个即能反映函数f（x）的变化特性，又便于计算的简单函数P（X），用P（X）近似f（x）。常用的插值方法有拉格朗日插值法、牛顿插值法、埃尔米特插值法、分段线性插值法、三次样条插值法。文中用一未知函数f（x）来反映某学校毕业生人数的变换规律，并根据2006年到2012年毕业生人数的原始数据建立多项式插值函数，借助MATLAB软件计算出2013、2014年的毕业生人数。并对这两种插值法进行了对比分析。得到拉格朗日插值法在这一问题较之三次样条插值法具有更高的精度。

1 插值法的定义

设f（x）是定义在区间[a，b]上的连续函数，x0，x1，…，xn是[a，b]上n+1个互不相同的点，φ是给定的某一函数类。若 φ 上有函数 φ（x），满足 φ（xi）=f（xi），i=0，1，…，n则称φ（x）为f（x）关于点x0，x1，…，xn在φ上的插值函数；x0，x1，…，xn为插值节点；称f（x）为被插值函数。

2 拉格朗日插值多项式

给定（xi，f（xi））（i=0，1，…，n）其中 xi互不相同，构造次数至多为n的插值多项式Ln（x）：

关于x0，x1，…，xn的n次拉格朗日插值多项式，它满足Ln（xi）=f（xi），i=0，1，…，n。

3 三次样条函数

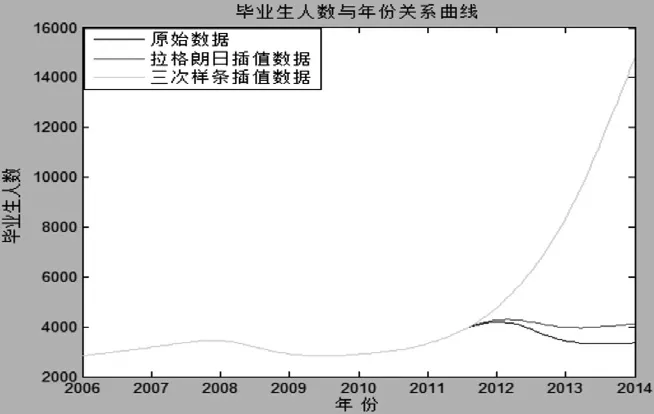
给定区间[a，b]上n+1个节点a=x0

4 示例

将拉个朗日插值与三次样条插值应用于实例分析。表1为某学校2006年到2014年毕业生的总人数。从表1中可以观察到毕业生人数与年份存在某种非线性关系。本文用一未知函数f（x）来表示这种非线性关系，以自变量x表示年份，函数值表示毕业生的总人数。将2006年到2013年这8组数据作为插值节点，分别运用拉格朗日插值法与三次样条插值法进行拟合，得到毕业生人数随年份的变化曲线。并将预测值与真实值进行比较。

表1 某学校年毕业总人数

以2006年到2012年的毕业生人数为7组数据对使用拉格朗日插值法进行插值，得到一个六次多项式函数Ln（x），以该函数表示毕业生人数与年份的非线性关系，具体函数曲线如图1所示。运用该函数对2013年的毕业生人数进行预测，得到2013年的毕业生人数为3875人，2014年的人数为4122人同样以2006年到2012年的毕业生人数为7组数据对使用三次样条插值法进行拟合，得到一个三次多项式函数Sn（x），具体函数曲线如图1所示，对2013年的毕业生人数预测得到7951人，2014年人数为14762人。2013、2014年毕业生真实数据与插值数据见表2。

图1 毕业生人数与年份关系曲线

5 结束语

由图1可以观察出拉格朗日插值数据比三次样条插值更接近真实值，三次样条插值表现出了龙格现象，用插值法对毕业生人数与年份的数据对进行插值时，拉格朗日插值法比三次样条插值法有更高的可靠性与准确性。

[1] 李庆扬，王能超等.数值分析[M].北京：清华大学出版社，2008.12.