基于通用滤波多载波系统的PAPR抑制算法

张 瀚，周 志，潘在峰

（1.中国联合网络通信有限公司三亚市分公司，三亚 572000；2.中国联合网络通信有限公司海南省分公司，海口 570216）

1 引言

无线智能终端和移动互联网的迅速发展，智能家居、智慧城市等新终端形态的出现，使得设备连接密度急速扩张，数据业务出现爆炸式增长趋势，移动通信系统正在向5G移动通信系统迈进。5G通信系统的关键能力指标更加丰富，对能效和频谱利用率等方面要求更高，对系统安全、传输时延和无线覆盖等性能的要求也明显提高了[1]。5G通信系统的发展已经成为业界研究的热点问题。

随着频谱资源的稀缺，5G通信系统迫切要求可以灵活有效地使用频谱资源，从而达到增加系统容量并提升数据传输速率的目的。4G通信系统的关键技术OFDM技术，由于该技术本身的一些固有特性，导致了低功率效率、时频同步要求严格、参数设置不灵活等问题。OFDM本身的固有特性使得它不适合5G通信系统中某些应用场景。在此背景下，利用数字滤波器组生成非正交波形的方案引起了研究人员的广泛关注。5G通信标准提出了通用滤波多载波（UFMC）、多载波滤波器组（FBMC）等候选波形。

UFMC波形与OFDM一样，也是由多个不同频率信号叠加而成。因此，UFMC系统的信号的幅度变化范围较大，存在高PAPR的问题。高PAPR是多载波系统中的突出问题，会使信号处于放大器的非线性部分，从而产生非线性失真，使得能量转换效率变低[2]。根据5G通信系统的能效要求可知，5G系统也要求低PAPR指标[3]。例如，电池移动终端对功率放大器的能耗要求高，低功耗的电池终端就要求系统的PAPR低。

为了解决多载波系统的高PAPR问题，目前有较多的PAPR抑制方案，但绝大部分是关于OFDM系统的PAPR抑制方案，少量关于FBMC系统和UFMC系统的PAPR抑制方案。常用的PAPR抑制方法主要分为限幅、编码、加扰和DFT等。限幅技术是对幅度值超过预设门限值部分的信号进行非线性处理，从而达到PAPR抑制的目的。文献[4]-[6]采用了实现方法简单的限幅滤波算法来解决OFDM系统的高PAPR问题，但是由于采用的是非线性处理，破坏了载波间的正交性，使得系统的BER性能恶化。文献[7]从理论上分析了UFMC的PAPR的性能；文献[8]提出了基于UFMC系统的PTS方法。

加扰技术是对传输数据块乘以旋转因子，然后选取具有PAPR值最小的数据块进行传输。该技术也不会引起波形失真的问题，但会随着子载波数量的增加导致实现复杂度急剧增加。针对PTS技术高复杂度高的问题，本文提出了低复杂度的PTS-Clipping联合算法来抑制UFMC系统的PAPR大小。

2 OFDM系统的经典PTS方法

图6-4给出了经典的OFDM的PTS方法的传输结构图。PTS技术是将OFDM系统的N个符号的输入数据块分成V个互不相交的子块，然后对每一个数据子块进行加扰[9]。第m个子块经过IDFT变换后变为每个子块乘以相应的复相位因子然后进行IFFT变换得到：

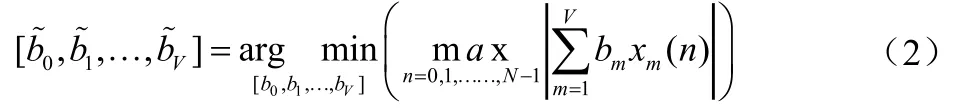
最小的PAPR向量时域信号可表示为：

在实际应用中，为了保证系统性能，通常设第一个子块的相位因子固定为1，即：b1。为了降低计算复杂度，在WV-1个有限的集合中搜索最佳的相位因子集合。因此，可知搜索复杂度是随着子块数量V的增加呈指数性增长。

3 系统模型

根据图1所示，通用滤波多载波系统是由B个子带组成，每个子带子载波数量为M，总的子载波数量为N，采用切比雪夫滤波器f，滤波器长度为Lf，在一个符号时间间隔内的基带离散时间信号为：

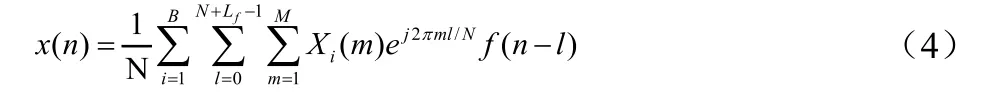
式中，输入数据Xi（m）是独立随机变量的比特流，以等概率均匀分布进行数字调制后得到的频域子载波信号，所有星座点的实部和虚部的均值为零，方差相等；x（n）是经过UFMC调制后得到时域输出信号；n为离散时间索引。

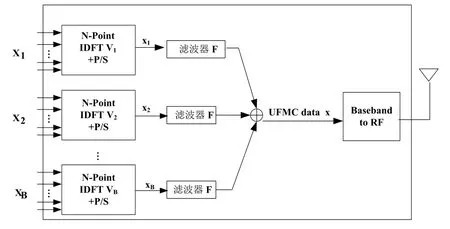
图1 UFMC系统发送结构图

UFMC的等效离散时间发送信号x（n）是所有子带独立随机变量子载波叠加而成，因而幅度变化范围较大，可能导致峰均功率比较大。一般用信号的峰值平均功率比（PAPR）来表示发送信号时域的变化特性。其定义为：

由于滤波器f的长度可能超过子载波的数量M，使得相邻的两个或多个符号之间不能相互独立，但UFMC和OFDM系统具有相同的传输速率，均在T时间内平均发送一帧复符号，可采用公式（5）近似定义PAPR。

由于PAPR是随机的，通常用大于特定门限值的概率估计系统的PAPR统计分布特性，称为互补累积分布函数（CCDF）为：

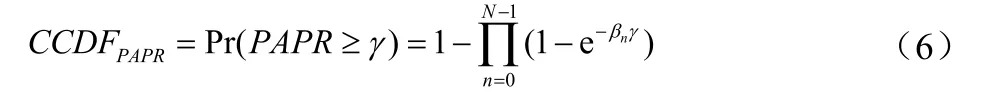
优化CCDF，可将最优化的问题可以描述为下式：

优化后，可得CCDF的最小值为[8]：

4 提出的UFMC系统低复杂度的PTS-Clipping联合算法

4.1 限幅方法

限幅方法是最简单的PAPR抑制技术，对大于限定门限的部分进行非线性处理，把发射信号的最大幅度限定在预设的门限值以内，幅度值未超过门限值的部分不做任何信号处理[10]。

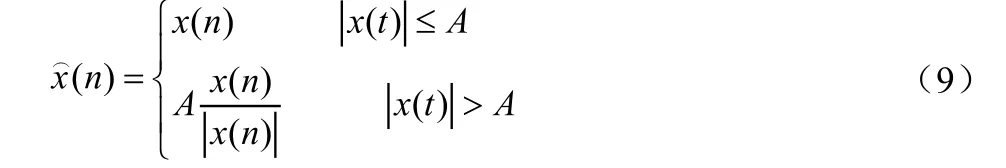
式中，A为预设电平门限值。限幅比（CR）是限幅电平与信号的均方根的比，在限幅算法中是很重要的参数，CR值越大，PAPR抑制效果越好，同时也使系统的BER性能恶化[11]。

4.2 低复杂度的PTS-Clipping联合算法

UFMC是将输入的子载波分为B个子带，每个子带单独进行IDFT变换，通过切比雪夫滤波器f后进行累加得到基带时间信号。PTS算法是对每一个数据子块进行加扰。由于UFMC系统将输入的子载波序列分为互不重叠的B个子带，可以直接对子带进行加扰。根据OFDM传统的PTS方案可知搜索复杂度随着子带数量的增加呈指数上升。为了降低搜索复杂度，如图2所示，将B个子带分为V个子块，每个子块含K个子带，可得：

式中，m为子块序列号；k为子带序列号；n为时间序列号。

为了降低PTS算法的计算复杂度，在处理相位加权时，充分利用相位加权序列与旋转因子的关系。首先，计算部分相位序列加权的同时保存对应候选序列；然后，将对应候选序列扩展为全部的候选序列。由于PTS算法是通过加扰对子载波进行重组，如果先采用限幅方法后再使用PTS方法，会对限幅算法的结果带来影响。因此，PTS-Clipping联合算法是首先采用PTS算法，然后再利用限幅进一步对PAPR进行抑制。算法步骤如下：

步骤1：根据相位加权因子生成WV-1种候选的相位加权序列。

步骤2：将相位加权序列分成W组。因为第1子块的加权因子恒定为1（即，b1=1），将第2子块的加权因子b2相同的序列分为1组。

步骤3：选取WV-1/2组加权序列，选取的发送序列中的加权因子b2不能互为相反数。

步骤4：求已选取的相位加权序列所对应的候选序列，并产生余下WV-1/2组相位加权序列所需要的相同项Zi，

步骤5：利用步骤4得到的Zi，只需要进行复数加法运算就可以得出剩下WV-1/2组的候选序列。

步骤6：比较得到的所有加扰后序列的PAPR值得出具有最小PAPR值的发送序列。

步骤7：检测得到加扰后得到最小PAPR序列的幅度值，并采用限幅算法，进一步减小PAPR的大小。

图2 基于UFMC系统的PAPR减小的低计算复杂度PTS技术框图

5 复杂度分析与仿真结果

5.1 复杂度分析

提出的低复杂度的PTS-Clipping联合算法由于利用了加权序列的特点，计算复杂度得到了大幅度降低。为了简化分析，均方根运算、平方运算和复数除法作为为复数乘法，对比和复数加法分别作为1次和2次实数加法[12]。PTS-Clipping联合算法的计算复杂度与PTS算法的计算复杂度对比如表1所示。根据复杂度对比一览表可知提出的PTS-Clipping联合算法的计算复杂度比PTS算法的计算复杂度低。

表1 复杂度对比一览表

5.2 仿真结果分析

本文对基于UFMC系统的低复杂度的PTS-Clipping联合算法、限幅算法和PTS算法的PAPR抑制效果进行了仿真。仿真参数如下：QPSK调制，系统子载波N=512，过采样因子L=4。

图3对CR为[0.8，1.0，1.2，1.6，2]的情况下的PTSClipping联合算法的PAPR抑制效果进行了仿真。通过仿真结果可知，当CR的值越大，PAPR抑制效果越好。但同时也会带来BER性能恶化的问题。如图4所示，随着CR的增加，BER性能不断恶化。

图3 不同CR的CCDF对比图

图4 BER性能与CR的关系

图5对低复杂度的PTS-Clipping联合算法、限幅算法和PTS算法的PAPR抑制效果进行了仿真。UFMC系统仿真参数为：子载波数量N=256，16QAM调制，过采样因子L=4，CR=1.2。根据仿真结果可知，提出的低复杂度的PTS-Clipping联合算法和限幅算法都可以较为显著地降低PAPR的值。PTS算法的PAPR抑制效果最差。但是，由于PTS-Clipping联合算法和限幅算法都采用了非线性方式进行PAPR抑制，因此PTS算法的BER效果是最好的。

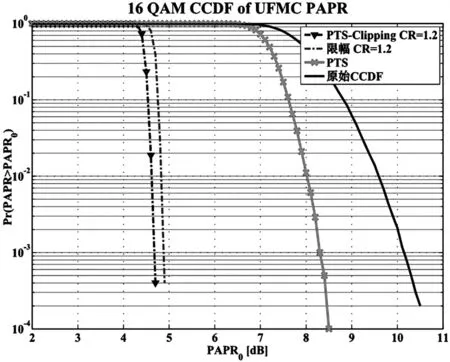
图5 不同算法的PAPR抑制效果对比图

6 结束语

本文提出了一种基于UFMC系统的低复杂度的PTSClipping联合算法。该算法的明显降低了经典的PTS算法的计算复杂度，PAPR的抑制效果比传统的PTS算法和限幅算法的效果都要明显，而BER性能优于限幅算法。

[1] 尤肖虎，潘志文，高西奇等.5G移动通信发展趋势与若干关键技术[J].中国科学：信息科学，2014，44（5）：551-563.

[2] L.Hanjo，M.Munster，B.J.Choi，et al.OFDM and MC-CDMA for broadband multi-user communications[J].WLANs，and Broadcasting，John，2003.

[3] S.Chen，J.Zhao.The requirements，challenges，and technologies for 5G of terrestrial mobile telecommunication[J].Communications Magazine IEEE，2014，52（5）：36-43.

[4] B.S.K.Reddy，B.Lakshmi.Experimental validation of orthogonal frequency division multiplexing with peak-to-average power ratio reduction and out-band distortion control using software de fi ned radio[J].IET Signal Processing，2016，10（2）：182-194.

[5] R.K.Singh，M.Fidele.An efficient PAPR reduction scheme for OFDM system using peak windowing and clipping[C].Third International Conference on Image Information Processing.IEEE，2016：491-495.

[6] Y.Wang，W.Chen，C.Tellambura.Genetic algorithm based nearly optimal peak reduction tone set selection for adaptive amplitude clipping PAPR reduction[J].IEEE Transactions on Broadcasting，2012，58（3）：462-471.

[7] Rong W，Cai J，Yu X.Low-complexity PTS PAPR reduction scheme for UFMC systems[J].Cluster Computing，2017，20（4）：3427-3440.

[8] Rong W，Cai J，Yu X.The research on peak-to-average power ratio of universal fi ltered multi-carrier system[J].Journal of residuals science & technology，2016，13（9）：1544-8053.

[9] S.H.Muller，J.B.Huber.OFDM with reduced peak-to-average power ratio by optimum combination of partial transmit sequences[J].Electronics Letters，1997，33（5）：368-369.

[10] S.K.Deng，M.C.Lin.Recursive clipping and fi ltering with bounded distortion for PAPR reduction[J].IEEE Transactions on Communications，2007，55（1）：227-230.

[11] 孙锴.MIMO-OFDM无线通信技术及MATLAB实现.北京：电子工业出版社，2014，190-195.

[12] J.Nam，S.R.Kim，H.K.Chung，et al.Cholesky based ef fi cient algorithms for the MMSE-SIC receiver[C].IEEE Global Telecommunications Conference.IEEE，2007：3045-3050.