经历“差错” 让成长自然发生
——《解决问题》中那些事儿
赵红亮(特级教师)
一个人的成长如果没有错误的洗礼,一定是不完整的人生,学习也一样。心理学家盖耶指出:“谁不考虑尝试错误,不允许学生犯错误,就将错过最富有成效的学习时刻。”课堂中学生的错,是天性,如何化“差错”为资源、为神奇,让学生于实实在在的跌倒和爬起来中经历思维的碰撞,经历心智的成长,显得格外重要。
在山西省“十二五”重点规划课题“培养小学生数学素养的研究”结题会上,山西省特级教师苏振希所执教的《解决问题》一课令人记忆犹新。此内容是人教版六年级上册《分数除法》中“用抽象的分数单位‘1’解决问题”(工程问题),意在让学生经历解决问题的全过程,在这个过程中积累解决问题的经验,提高解决问题的能力。
【片断一】
出示情境图:

师:学校附近要修一条路。甲队单独修12天可以修完,乙队单独修18天可以修完。学校要尽快修完怎么办?
生:两队合修。
师:合修这条路,需要多少天呢?
生:没有告诉全长。
师:条件不够?怎么解决?
生1:列方程解决。
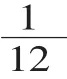
生3:可以假设这条路的长度。
师:知道了这条路的长度,就可以解决了吗?你想让这条路多长呢?
学生七嘴八舌:360千米……400千米……420千米……
学习卡
假设这条路长____千米。
甲队每天修多少千米:____。
乙队每天修多少千米:____。
两队合修,每天修多少千米:____。
两队合修,需要多少天修完:____。
综合算式:____。
师:试一试,看一看你能发现什么?有困难你也可以按照上面学习卡的提示来完成。
(学生自己尝试、探究之后,全班交流)
生1:我认为两队合修15天完成。
12÷2+18÷2=6+9
=15(天)
生2:这样合修15天,还不如让甲队单独修。
师:合修是什么意思?
生1:合修就是你修一半,他修一半。
生2:不对,合修就是两个队一起做,要节省时间,你节省时间了吗?
生1:是有问题。合修是两队一起做,不是一人一半。
师:表扬这位同学!敢于把自己的想法分享给大家,给大家思辨的机会。
【思考:“规避”还是“直面”错误?学生对“合修”提出不同的理解。我们的习惯思维是要在课堂的第一次汇报时给学生提供一个相对正确的结果,给学生建立一个正向的表象,这个错例怎么给,什么时候呈现?在这里学生错误的呈现如一石入水,激起思维的涟漪,辩论中学生一步步厘清了合修的含义,在辨析中学会了寻找问题的本源,明确了进一步探索的方向。同时教师对提供错误的学生进行了鼓励,使学生在自主思考和交互学习中不断修正自己的想法,这种跌倒了再爬起来的经历显得弥足珍贵。
所以,错误在什么时候出现并不重要,重要的是抓住学生的困惑点,让学生在学习中学会内省和自我提高以及在开放宽松的环境中让学生不畏惧错误也不回避错误。】
【片断二】
师:我们接着交流。
生1:我假设360千米。
师:为什么选这个数?

(师生对此画图,进行二次分析)
生2:我假设这条路72千米,后来又假设36千米,算出的结果都是7.2天。我发现假设的长度不同,结果却是相同的。
师:继续验证。假设这条路长470千米,你能算一算吗?
生3∶如果假设这条路长470千米,结果仍然是7.2天。
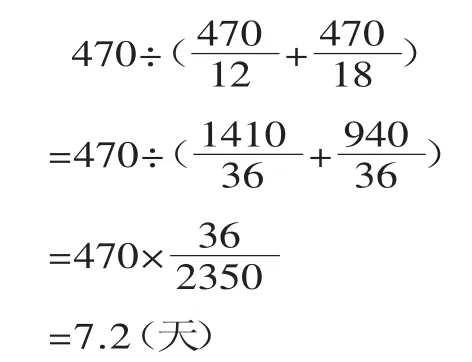
师:发现什么了?
生:无论能不能除尽,答案都是一样的。
师:为什么?
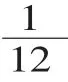
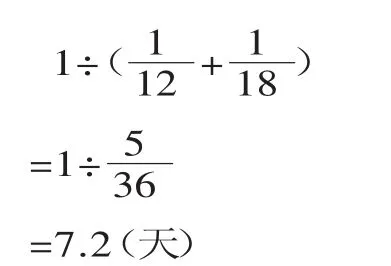
师:谁听懂了?可以解释给大家听吗?
(师生一边画图一边讨论)
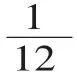
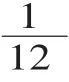
师:观察你们研究的过程和结果,结合线段图,它们有什么相同点和不同点?
生 7:36 千米、360 千米、72千米、470千米,假设的总长度在变化,甲乙两队的工作效率也随之变化,但合修的天数不变。
生8:假设的路程虽然不同,根据商不变的性质,被除数和除数同时乘或者除以相同的数(0除外),它们的商不变。
师:路程变化,每天的工作量也随之变化;但每天的工作量与路程的分率关系不变,也就是工效的分率不变;两队每天合修的长度占总长度的几分之几就是不变的。
师:你会采用哪一种方法来解决此类问题,为什么?
【思考:怎样的经历更有效?如何设计有效的活动让学生主动经历,使思维拾级而上?本环节的难点在于让学生理解用抽象的单位“1”解决问题,实现从具体到抽象、由变到不变的跨越,经历自主建模的过程,积累问题解决的活动经验。课堂中让学生思维实现三级跳:1.假设这条路总长360千米,通过具体有形的数量让学生初步感知;2.假设这条路总长470千米,当无法整除时,迫使学生用到了分数,进一步理解,要解决合作的时间,就必须用“工作总量÷工效和”。3.当工作总量不知道的前提下,假设全长为单位“1”。在探讨“变与不变”的基础上,通过逐层深入的交流探讨,感悟“合修时间不因工作总量的变化而变化”的实质缘由。】
【课后思考】
一、在经历问题解决的过程中,让学生的经验渐次生长
整节课,让学生经历“提出问题——阅读与理解——分析与解答——回顾与反思”的过程,经历运用“假设法”的活动过程,真切感受假设法是解决问题的重要策略,在经历矛盾冲突中尝试借助各种策略去解决矛盾,比如采取数形结合的方式去理解数量关系。使学生的问题解决能力在这个过程中逐步提高。
二、在经历“差错”中,让学生的成长自然发生
学生课堂中的“差错”是可遇不可求的,“差错”往往是学生认知的模糊区和盲区,这个时机稍纵即逝。有效合理地运用“差错”,让其变成宝贵的教学资源,是每个教师的必备能力之一。本节课抓住学生的错误,并借助充分的讨论和交流,暴露学生的思维过程。通过辨析,使学生在自我反思中进行自我纠错,经历自我否定的过程,这个过程是学会反思的过程,也是学生心智成长的过程,更是每一位学生共同参与成长的过程。将这样的过程放大是必需的,也是需要我们教师付出心血和智慧的。

