引导学生从整体的角度理解数学概念——《认识小数》教学设计及解读

朱国荣 王 扬

【教学内容】

苏教版三年级下册第100页。

【课前思考】

本课是学生第一次认识小数，是对数系认识的一次重要扩展。它与整数相比，在意义、书写形式、计数单位、计算法则等方面有某些相同的地方，但也有一定的差异。教材先安排认识整数部分是0的小数，再认识整数部分不是0的小数，最后介绍小数各部分的名称。虽说是初步认识，但我们就仅仅停留于会认、会读、会写小数这些零碎的知识“点”吗？我们知道，没有正式学过小数的学生，在生活中或多或少对小数知识已有了一定的感性认知。面对这样的情形，如果目光仅仅局限于这些知识点的认知，学生所获得的也不过是些基础性的知识，其丰厚的数学内涵会大大缩水。我们可以更深入地思考，为什么要学习小数？它与分数、整数有什么联系与区别？小数本身的特点与价值在哪里呢？

带着这样的思考，我们重新审视这节课的教学设计，对教材现有内容进行取舍与改造，将本节课分为三个板块：“分”，小数出现了；“合”，小数变大了；“分分合合”，小数变多了。这三个板块，成为教者雕琢、展开的基点，避免浮于表面的知识点流程的教学。这些点在情境设置、师生交流、问题突破中逐渐丰满成一个个板块，板块名称从学生角度拟定，通俗易懂。

这三个教学环节层层递进、自然流畅，呈现了知识发生、发展的过程，展现了一个丰富而完整的知识链条。与此同时，在教学的过程中，教师引导学生感悟了整体的思想，学会了从整体的角度去审视问题、分析问题、解决问题，从而使他们的思维得到了拓展，智慧得到了增长。

【教学过程】

板块一：“分”，小数出现了。

1.整数→分数→小数。

师：（出示长方形）这是什么图形？（出示直尺）长是多少？宽呢？

师：（出示另一个长方形）老师这儿还有一个长方形。你还能像刚才那样一口报出它的准确长度吗？

师：为什么不能？（因为长不足一分米）

师：借助我们以往的学习经验，不足1分米时，我们可以用什么办法表示出它的准确长度呢？

生：用厘米作单位。

生：可以用分数来表示。

师：不管是用厘米作单位，还是用分数来表示，我们都是把这1分米怎样？

师：（出示板块标题“分”）怎么分？（把1分米平均分成10份）

师：为什么平均分成10份？（1分米等于10厘米）

师：长是多少？如果用分米作单位呢？可以用我们学过的哪个数来表示？宽呢？

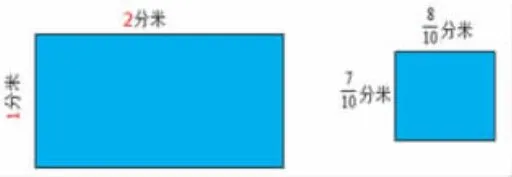
（1）比较：刚才我们测量了两个长方形的长和宽，都是用分米作单位，为什么第一个长方形的长和宽可以用整数表示，而第二个长方形的长度却要用分数来表示？

（2）小结：当不足1分米的时候，我们就把1分米分一分，用分数来表示。除了分数，还可以用新的数——小数来表示。

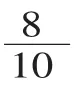
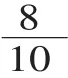
（继续出示板块名称：，小数出现了）

师：今天我们就一起来认识小数。

【设计解读：教学中只有引发心理冲突，让学生在解决问题中感受到认知矛盾，才能体会小数出现的必然性。学生根据自己的经验会想到继续更小地分，突出了关键词“分”。学生发现在实际生活中还需要比单位1更小的计量。透过“分”，我们因需要而看到数的扩展、认知的迁移。】

2.小数的读写、意义。

（1）读写。

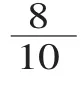
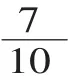
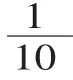
（2）意义。

师：0.4分米表示哪一个分数？你能画图表示出0.4分米吗？

（学生上展台反馈）

师：为什么不选图一？（小数和分数一样都必须建立在平均分的基础上）

师：为什么不选图二？（我们今天学习的小数都是把“1”平均分成了10份）

师：（PPT去除图一图二，保留正确的图三）像这样把1分米平均分成10份，1份是多少？（0.1分米）现在呢？十分之四分米，也就是0.4分米。

师：0.4分米是怎么来的？（把1分米平均分成10份，取其中的4份）

师：原来0.4和十分之四的意义是一样的。谁再来说一说？0.4里有几个0.1？

【设计解读：本环节教者设计了3个别具匠心的直条图，让学生用已学过的分数知识，对3个直条图的特征进行重新审视，从“平均分”到“平均分成10份”，学生在不知不觉中逐步建构，接近了0.4的本质，完善了认知体系。】

（3）分数与小数的联系。

师：现在我们一起把刚刚用到的分数和小数整理在一起。

比较：仔细观察，左边的分数和右边的小数有什么联系？同桌讨论一下。

师：你能再举出一组这样的例子吗？

小结：十分之几就是零点几，零点几也可以写成十分之几。清楚道出了今天所学的小数和分数之间紧密的关系。带着我们的发现，玩个抢答游戏。

看图说小数。

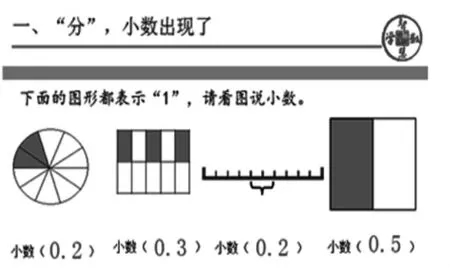
师：这几幅图分别用哪些小数表示呢？

师：图1和图3有些不一样，为什么阴影部分都表示0.2？有什么相同点？

生：图1是把一个圆看作“1”平均分成10份，图3的”1”表示一条线段。

师：1还会是什么样？（所有图形）除了图形，物体可不可以？比如蛋糕？

小结：不管什么样子的“1”，只要平均分成了10份，取出几份就是零点几。

师：最后一幅图用哪个小数表示呢？为什么是0.5？ 表示0.1的图又是哪个？

【设计解读：本环节教者精心创设了“看图说小数”的游戏活动，将小数、分数知识有机地融为了一体。通过数形结合，学生在对图形的比较、争论中，慢慢逼近小数的本质，深刻感受到小数与分数间的联系。】

板块二：“合”，小数变大了。

师：0.8、0.2 都小于 1，小数都比1小吗？

1．认识比1大的小数。

出示：

固体胶是多少元？你能试着用小数表示吗？

师：2角为什么是0.2元？

小结：1元和0.2元合起来就是1.2元。你看他在用一种新方法找到小数了。

师：（课件出示：合）他把整数1元和小数0.2元合起来得到一个新的小数1.2元。

师：1.2还比1小吗？你能用画图表示出来吗？

师：（出示1个正方形）如果这个正方形表示1元，用它能表示出1.2元吗？够吗？（出示第2个正方形）你打算怎么涂色表示1.2，和你的同桌商量一下。

师：根据图，谁再来说一说1.2是怎样合成的？ 现在变成了什么小数？（课件演示逐个增加一份，让学生说出小数：1.3、1.4、1.5、1.6……2，10个 0.1 又合成了1，加上前面的整数1，所以是2）

师：如何用涂色部分表示出2.1元呢？（图形表示：整数2和小数0.1又合成一个小数2.1）

2．介绍小数各部分的名称。

出示：

师：文具盒是多少元呢？怎么想的？

师：刚才我们合成了小数1.2和3.5，小数小数，是不是都很小

啊？看一看。

出示：

师：2999元9角=2999.9元。它是小数吗？它小吗？一起来读一读。

师：它是怎么合成的呢？谁来说一说。（2999.9元是由2999元和0.9元合成的）

小结：看来通过“合”，我们也可以得到一个比较大的小数。

师：这些小数中间都有个小圆点，我们把它叫做小数点，小数点左边的部分叫做整数部分，小数点右边的部分叫做小数部分。

小结：整数与小数是相通的。合起来，小数变大了。

【设计解读：小数和整数都符合“十进制记数法”的计算规则。分数和小数都是以平均分为基础的，可以说整数、分数、小数之间有着千丝万缕密不可分的联系。第二板块中突出关键词“合”。教学中紧扣分数和小数对应改写，突出对小数意义的概括性理解。学生自主发现，把整数和纯小数“合”起来，小数有时也不小呀。在这个板块，学生发现“合”也是一种新的表示小数的方法，通过“合”，从纯小数到带小数，进一步丰富了学生对小数的认识，让学生感受到数学的统一与和谐，逐步展现了一个全面而丰富的客观世界，在这其中，学生开阔了视野，提升了认识，明辨了思想，生发了智慧。】

板块三：“分分合合”，小数变多了。

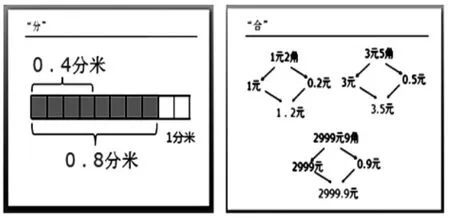
师：回忆一下，课一开始，我们怎样选用直条来表示0.4分米？

生：把这个直条看作1分米，平均分成10份，其中的4份表示0.4分米，8份表示0.8分米，我们通过“分”得到了小数0.4、0.8。

师：1元2角我们又是怎么把它写成小数的呢？

生：我们通过“合”的方式把1和0.2合起来就是小数1.2元。

小结：通过分，我们得到了这些小数；又通过合的方法，找到了这样的小数。分分合合，小数变多了。

师：老师带来一条神奇的直线。这些数是小数吗？

师：像 1、2、3、4、5 等表示物体个数的数是自然数，0也是自然数。它们都是整数。

师：在这条直线上，你看到了几个数？直线上只有5个数吗？

师：你能用数学的眼光找到小数吗？比如0—1之间？

（先把0—1之间平均分成10份）

（学生上台演示：找出0.1—0.9）

师：通过“分”，在 0-1 之间可有序地找到这么多的小数，真棒！他找到的都比1小，谁能找的比1大的小数吗？

师：怎样可以快速找到2.9的位置。（2-3之间，接近3）100.9在哪两个整数之间？

小结：虽然屏幕上看不见，但我们想象可以推理出来，越往右数越来越大。

师：下面玩个猜数游戏。

这个数在3-4之间，可能是多少？（3.6）

师：这个数还在3-4之间，比3.6大，可能是多少？（3.7）

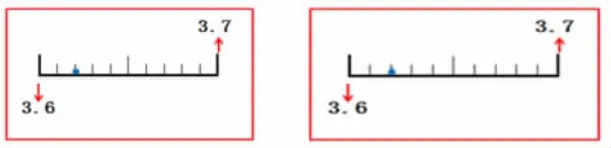
师：（出示一个点）这里是几？这里能用3.6表示吗？能用3.7表示吗？

师：有什么办法可以准确表示它的位置呢？

师：就要把3.6-3.7这段怎么办？（再平均分成10份）

师：3.6-3.7这段平均分成10份，现在可以准确表示了吗？在3.6和这个数之间还有小数吗。还有很多很多呢。

小结：像这样，我们还可以继续分下去，得到的计数单位越来越小，精确的程度也越来越高。整数、分数、小数都可以在这条直线上找到自己的位置，它们之间有着紧密的联系。分分合合，有小有大，我们发现数越来越多，越来越密了。

【设计解读：这个板块中突出关键词“分分合合”。从小数的产生，体验数系的扩充过程；从小数这一特定的内容，沟通整数、分数和小数之间的内在联系；从发现3.6和3.7之间的“空隙”使我们得到的计数单位越来越小，精确的程度也越来越高，小数使我们的计数更精确。“分”，小数出现了；“合”，小数变大了；“分分合合”，小数变多了。环环相扣，层层递进。这一系列看似平常的学生活动，却将知识脉络清晰地铺陈开来，引发学生自由思考、自觉起疑，促进学生思维向深度发展。从零散到完整，从朦胧走向清晰，从清晰走向深刻，展示了人类认识事物的过程，蕴含了数学学习中逐步提升的智慧。本课设计早已跳出了以往的教学模式，将问题开放化，有很大的包容性和可选择性，让人不由想起康托的话“数学的本质是自由的”。】