合理选材:促进图形概念建构的“良方”
——以《角的初步认识》为例
林俊 沈璐
概念形成和概念同化是数学概念学习的两种方式。由于小学生知识经验较少、思维能力薄弱,概念形成自然成为他们学习概念的主要途径。掌握数学概念的完整历程,意味着概念形成后,须经概念内化,直至概念建构。在教学数学概念的过程中,如何选择学习素材,选择哪些学习素材至关重要。而学生掌握数学概念,并不是一蹴而就的,它是一个不断深化,甚至是曲折反复的过程。下面以苏教版《角的初步认识》为例,结合杨婧、胡彩云两位青年教师的不同教学设计,谈谈如何选择学习素材,促进学生图形概念的建构。
一、同构的素材,着力图形概念的形成
“感知材料——观察比较——归纳提炼——抽象命名”是概念形成的一般教学流程。杨老师的设计就是按照这样的逻辑展开的,符合处于具体运算阶段初期的低年级学生以具体、形象为主要思维特征的认知规律。而胡老师的设计却跳出了这种思路,她别出心裁地从折直角模型切入教学。
从概念形成的一般流程可以看出,感知材料是概念学习的首要环节。那么提供的学习素材的数量、种类、性质等,就直接影响学生数学概念形成的品质。纵观以往设计的多种角的引入环节(有让学生从主题图中找角的,有让学生举例说生活中角的),看似注重了数学与生活的联系,实质是对学生知识经验了解不够。
我们曾经对全班学生进行前测,调查表明:他们看到“角”字,绝大多数联想到的词语是几角钱、牛角、羊角、角色、三角形、角落、墙角等,只有四人知道直角,不足全班人数的10%。说明学生头脑中与角有关的生活概念远远多于角的科学概念,并且他们对角的科学概念的认识并不是全面的、完整的,而是局部的、片面的。这时让学生进行指角活动,不仅指不准,也没有判断的依据,只是徒劳。在让他们“画出心中角的样子”时,接近一半的学生画的是三角形、四边形。说明学生不能区分角与三角形、四边形,只是对角有模糊的认识,还没有形成角的独立于多边形的正确表象。有近四分之一的学生能够画出角的图形,并且多数画的是锐角,对直角、钝角了解不多。在与部分学生交流时,发现他们往往把角的顶点看作角。
杨老师对学情了如指掌,选择从学生佩戴的红领巾入手,非常契合学生经验的现实起点。从前测统计数据可以看出,无论“想到的词语”还是“画出的图形”,学生对平面图形都情有独钟。“为什么叫三角形?”激活了学生的生活经验,将陌生的知识学习建立在学生熟悉的生活经验之上,角的概念引入显得十分自然、快捷。“角是一个什么样的图形?”则将学生引入新知的学习领域。
学生对三角形印象深刻的原因,无外乎两点:一是在一年级刚刚初步认识三角形等平面图形,有经验;二是生活中三角形的物体特别多,如学具三角尺、红领巾等,有表象。所以,角的认识从学生熟识的、常用的红领巾开始,是十分明智的。
为了便于学生建立角的完整表象和抽象角的特征,杨老师设置了连续而递进的指角、找角、析角等活动环节。学生指角,往往只是指角的顶点。教师深谙此情,故意放大错误,当呈现放大的一点时,学生忽然发现错了,再指出角的两条边。这样,角的图形正确表象的形成,不是源于教师的传达,而是来自学生主动的自我反思与自觉调整。找角,一方面是促进学生将习得的找角经验迁移到新的情境,另一方面是丰富角的样式,扩大角的外延,为后续概括角的特征提供全面的、多样的素材。析角是从物体中一一剥离、隐去无关的信息,从中透析、抽离出角的要素,使学生初步直观地认识角的标准图形,完整地感知角的不同形态。
课中生成的角虽然数量不多,但是很有代表性、同构性。有锐角、直角、钝角,有标准图形,还有变式图形,这些角尽管大小不同、位置不同、形状各异,但是都具备角的共同特征。由于有了之前的找角、指角、描角等细腻的感知过程与丰富的经验累积,面对问题“这些角的形状有什么相同的地方?”学生的回答“都有一个尖尖的地方”“还有直直的线”虽显幼稚,但也直逼角的图形之外在表征。教师因势利导、顺势而为,及时指出“尖尖的地方是角的‘顶点’,直直的线是角的‘边’”,将学生不规范的日常语言上升到约定的数学语言。而学生对角的特征的迅速把握源于对不同大小、不同形状角的共同要素的洞察。至此,角的特征的提炼可谓水到渠成、瓜熟蒂落。
胡老师并没有为学生直接提供观察的素材,而是从折直角模型切入,让学生经历直角的形成过程,在此过程中,自然地认识直角的名称和直角的特征(有一个顶点和两条边)。接着以此为实物模型,作为比较标准,让学生回到现实生活中,寻找生活中的哪些角和直角一样大,哪些比直角大,哪些比直角小。这样的设计将角的大小教学融入其中,一方面渗透了直角与锐角、钝角的关系及判断标准,另一方面自然过渡到“角的大小与什么有关、与什么无关”的学习。此后,才进入角的特征的学习。
可见,学习素材的选择,受制于学生的学习经验,也会影响教学内容的学习顺序。
二、变式的素材,助力图形概念的内化
掌握概念,实质上就是掌握同类事物的共同的关键特征(概念的内涵),也意味着能区分概念的肯定例证与否定例证。如果说概念的肯定例证传递了最有利于概括的关键信息,那么否定例证则传递了最有利于辨别的信息。一切包含有概念的共同关键特征的事物,叫概念的肯定例证。一切不包含这种共同关键特征的事物,叫概念的否定例证。我们不仅要运用肯定例证的变式,也要运用否定例证以促进概念的学习。
概念的形成是教学的重点环节,要引导学生对所提供的感性材料进行观察、比较、分析、抽象、概括,揭示概念的内涵和外延,进而形成概念。在这一过程中,我们要特别注意变式的运用,它可以使学生更好地区分事物的各种因素,并确定哪些是主要的、本质的,哪些是次要的、非本质的,对学生领会概念具有事半功倍的效果。两位教师都从实物图中抽象出三个变式的角的图形,这三个角的大小、位置、边长都不一样,变换材料的呈现样式,提出核心问题:这三个角的相同点和不同点是什么?引导学生排除非本质属性的干扰,紧紧围绕概念的本质属性进行观察,抽象出正确的概念。
学生对数学概念的掌握,不仅要经过概念形成的过程,而且还要经过概念运用的过程。在运用中检验学习效果,深化理解水平。两位教师在教学中,不约而同地从两个不同的层面帮助学生把握角的本质属性,理解角的内涵和外延。
首先,直接运用角的特征去判断一个图形是否是角。两位教师在图形呈现的数量上还是有区别的。杨老师提供的图形比胡老师多,并且比教材增添了一个图形,一增一减,对角的概念内涵和外延的识别力度上还是有差别的。“增”丰富了否定例证的类型,使学生感悟到“不是”角的原因可能是不同的:没有顶点、一条边是弯的、两条边都是弯的,只要其中一点不符合,这个图形就不是角;通过对多个角的肯定例证的判断,使学生感悟到“是”角的理由一定是相同的,即“角有一个顶点和两条边”,而与角的形状、大小、位置无关。这是对角的内涵初级水平的辨别。
其次,在复杂的情境即变化的图形中识别角。由于边、角不同的组合方式形成的变化结构和复杂图形,加大了学生对角的识别与辨析的难度,这是对角的内涵较高水平的辨别。无论哪种水平的运用,概念的肯定例证是从正面强化了角的内涵,否定例证则从反面突出了角的本质。学生对角的内涵的理解既是在否定例证的衬托中不断清晰与稳定的,也是在复杂情境的识别中不断丰富与加深的。
掌握概念,不仅要能区分概念的肯定例证与否定例证,而且要能区分概念的有关特征与无关特征。一类事物既有有关特征(本质属性),它决定着事物的分类;也有无关特征(非本质属性),它虽然不决定事物是否属于某一类,但处理不好,会对学生数学概念的学习形成干扰。利用好,可以促进学生数学概念的精确分化。
操作活动这种显性、外化的方式,能够反映学生对数学概念隐性、内化的程度。对角的内涵的认识,除了不断突出其有关特征(本质属性)“有一个顶点和两条边”外,杨老师提供了多种多样、难度不同的制作材料,让学生根据自己的能力选择,照顾了学生的差异,使角的表征方式更丰富。简明具体的活动建议,既有分工要求,又有做法提示,还有合作提醒,真是贴心又温馨。学生从大量的刺激模式中(角的大小、方向、材料、颜色等维度的相关素材),辨别角的这些非本质属性,发现体现概念特征的刺激模式。可以说这些概念的非本质属性是概念的肯定例证在无关特征方面的变化。通过变式,获得的概念更精确、稳定和便于迁移。
相对而言,胡老师变式素材的运用主要体现在角的概念形成阶段,在图形概念理解、内化上使用不多。
三、丰富的素材,促进图形概念的建构
奥苏伯尔认为,教材最佳的序列,要反应知识的逻辑结构,体现不断分化和综合贯通的原则。学生角的概念的学习过程,不能止于能够理解本质属性与非本质属性,识别标准图形与变式图形,还要能与邻近的其他数学概念区分,与相近的日常生活概念辨析,同样应该体现不断分化和综合贯通的原则。不断分化使学生对角的认识更精确,综合贯通使学生对角的认识更开阔。
如果两位教师在课的最后,再安排角与其他平面图形、相近的日常生活概念辨析,则会锦上添花。具体设计如下:
片断1:
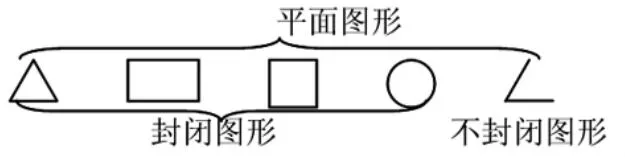
(出示三角形、长方形、正方形、圆和角的图形)
师:角和这些图形一样,都是平面图形。你们能看出角与这些平面图形有什么不同吗?
生:前面几个图形是密封的。
生:角有一处缺口。
师:也就是说角是不封闭图形。那么,这些图形就是——
生:封闭图形。
课件出示:
片断2:
师:我们课前调查,看到“角”字,大家主要想到这些词——(呈现:几角钱、牛角、羊角、角色、三角形、墙角等)今天学习的角与它们相同吗?
生:几角钱是关于人民币的,与今天学习的角不同。
生:牛角、羊角的边是弯的,与数学上的角不同。
师:角色是电影或戏剧中扮演的人物,与数学上的角不同。
生:三角形虽然不是角,但其中有三个角。
师:原来数学图形中藏着角,三角形就是根据它其中角的个数命名的。所以,三角形与数学上的角是有关系的。
生:五角星也是。
师:说得好!那么,墙角中有角吗?(出示图形)有几个?
(学生意见不一)
师:到底是几个呢?我们来看一看。(课件演示)
上述片断1将本课学习的角的概念与之前学习的三角形、长方形、正方形、圆一起纳入到上位概念平面图形之中,形成认知组块,便于记忆和提取。同时,引导学生观察,区分两者的不同,又将角的概念与平面图形中的其他封闭图形分化开来,从而形成稳定的、清晰的和可辨别的认知结构。
片断2目的在于区分角的日常概念与角的数学概念。如前所述,学生经验中存在很多与角有关的概念,它们对角的数学概念学习有的起阻碍作用,有的起促进作用。学习角的数学概念后,很有必要进行辨别与沟通。

