一种基于有向图的配变轮换序列自动生成方法

胡 蕾， 辛建波， 范瑞祥， 夏永洪， 纪清照

(1.国网江西省电力公司电力科学研究院 江西 南昌 330096； 2.江西师范大学 计算机信息工程学院 江西 南昌 330022)

0 引言

各县市供电公司在夏季、冬季等用电高峰来临之前，都要根据历年情况对配变的峰值负荷进行评估，对超载、过载严重的配变改造，更换型号或更换更大容量配变[1-3]，提高配变运行安全性.部分更换下来的配变尚未到使用年限，经评估后还可再利用[4]，更换下来可再利用的配变可在全县市范围内进行调配，有利于提高配变资产的价值，避免不必要的设备闲置[5-6].因容量变化引起的配变使用位置的变化，形成了配变轮换.国家电网部分县市供电公司自2011年开始采用配变轮换方法，采用“阶梯式”、“推磨式”等方式，按“大换中、中换小”策略[7]，对上百台重载、过载配变进行增容和轮换，以降低配网改造成本.

目前各县市供电公司的配变轮换方法多基于实践经验，采用“阶梯式”或“推磨式”方式对配变轮换，但配变轮换次序的求解与优化还未有较好的理论方法，缺少对配变轮换需求有效的描述方法，未能估算出轮换过程需新增的配变数量及轮换后闲置的配变数量.

本文利用有向图来描述配变轮换的需求，采用单向路径、最大环路和最长路径等方式来获得配变轮换次序，在满足配变增容改造的需求下，尽可能减少新增配变、闲置配变和借用配变需求，尽可能减少配变拆装次数，并通过某县市公司配变改造分析“阶梯式”、“推磨式”方式下配变轮换序列求解.

1 有向图描述模型

从供电可靠性和配变运行经济性等考虑，配变改造主要采用增容、减容和并列等方式[8]进行，容量的增减形成容量变迁关系.图论中的有向图是一种描述事物关联性的方式，能以简单、直观的方式增减节点或有向边，改变有向边方向[9-10]，电力系统中采用有向图、树形图等对电力调度、电力传输等进行描述[11-13].配变轮换过程是容量迁移以及迁移路径的问题，本文采用有向图来描述配变容量的改变需求，并将轮换次序求解转化为在有向图G=(V,E)中寻找最优路径的问题.

1.1 有向图

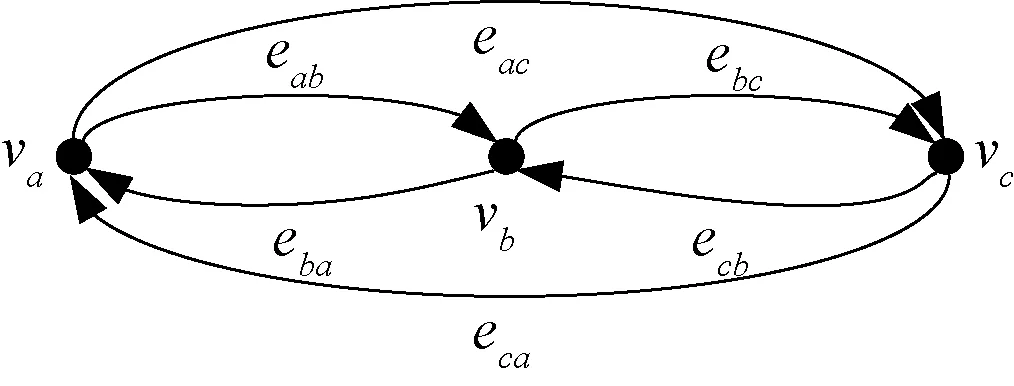
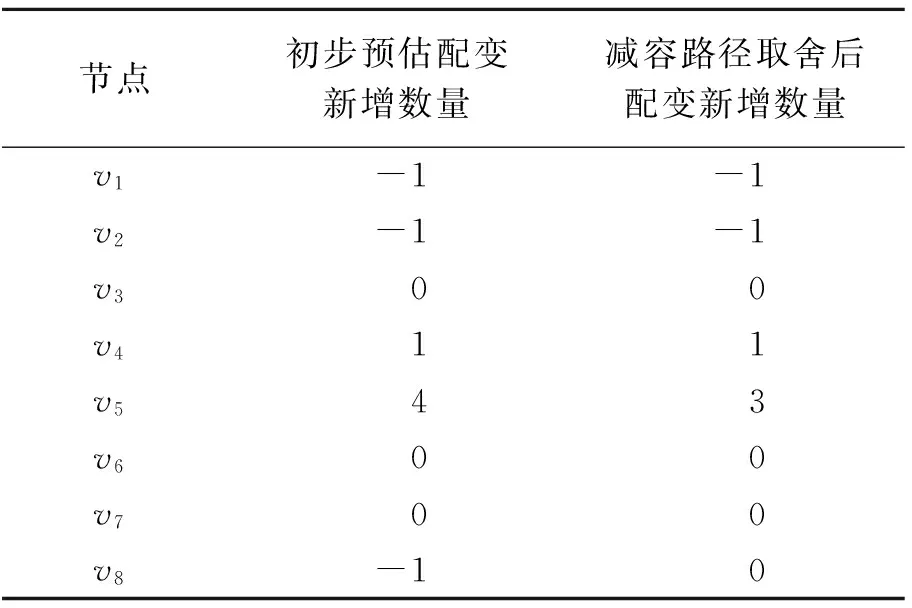
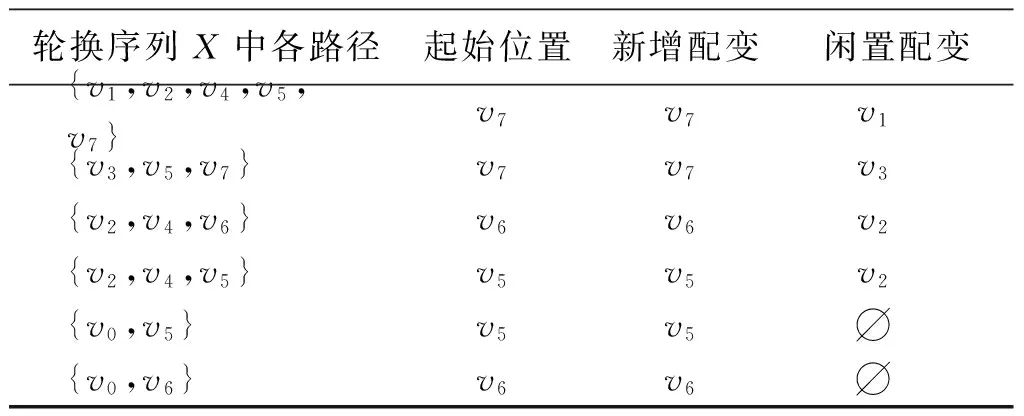
假设有n种容量的配变参与轮换，容量的大小顺序为c1,c2,…,cn(ci

由于存在多台相同容量的配变向另一相同容量增容或减容，因此所建立的有向图G中两个节点间允许存在多条边现象.同时,考虑到配变改造中，配变增加容量的需求相对于减少容量的需求有更高的优先权，按照方向将边分为增容边和减容边.某处的配变容量需要从ci更换到cj时，如果cicj，则边eij为减容边.

1.2 邻接矩阵

建立有向图G对应的邻接矩阵A=(aij)(n+1)×(n+1).

(1)

其中：k为顶点vi邻接到顶点vj边的条数，表示存在k台配变的容量需要从ci更换到cj.可以看出，A的上三角形为增容边，A的下三角形为减容边.

1.3 轮换序列

轮换序列X是有向图中p条路径的集合，X={P1,P2,…,Pp}，每条路径Pi是一个轮换次序.对于路径Pi={vi1,vi2,…,vil}(i=1,2,…,p)，可按节点vil,…,vi2,vi1顺序对相应容量的配变进行轮换.假设节点vil,…,vi2,vi1所对应容量为cil,…,ci2,ci1轮换，依次用cil换cil-1，用cil-1换cil-2，直到用ci2换ci1.此时,需要一台cil容量的配变来启动该轮换次序，且轮换后会剩余一台ci1容量的配变.因此完成普通路径的轮换次序，需要新增一台首节点对应容量的配变，会闲置一台末节点对应容量的配变.若路径Pi是环路,cil=ci1，环路起始节点可以为路径中的任意节点，可利用一台cij(j=1,2,…,l)容量的配变来启动该轮换次序，轮换后仍然会剩余一台cij容量的配变，我们称这个cij容量的配变为借用配变.

求解轮换序列时可根据不同策略和约束条件获得不同的路径集.配变轮换序列求解难度在于：有向图的多边特性；路径没有固定的起点/终点；没有顶点不重复的要求，但有边不重复使用的要求.

2 配变轮换模型

2.1 “阶梯式”和“推磨式”轮换方式

“阶梯式”配变轮换方式主要是“以大换中，以中换小”，达到“中小”容量配变被“大中”容量配变替换的目的，实现了中小容量配变的增容.“推磨式”配变轮换方式同时考虑中小容量配变增容和大中容量配变减容两个方面，此时，大换小与小换大可以实现循环，更利于降低配变改造成本.配变改造时,可根据配变增容、减容数量以及配变安装、停电成本等综合考虑选择轮换方式.

2.2 轮换路径分析

在利用有向图求解“阶梯式”和“推磨式”轮换序列时，“阶梯式”配变轮换序列路径主要涉及增容边的全覆盖，“推磨式”配变轮换序列路径不仅涉及增容边的全覆盖，还可以利用减容边形成环路和最长路径，从而减少新增配变的需求.因此轮换序列路径求解主要包含单向路径子集、环路径子集和最长路径子集求解.

2.2.1增容/减容单向路径子集求解 采用有向图中两节点连通性的求解算法，即布尔矩阵运算求解有向图可达矩阵算法，分析两节点间的连通性.因建立的有向图为多边连通图，首先取A的上三角形或下三角形，然后将A改为布尔矩阵，并求解最长的增容/减容单向路径.连通的两点之间存在多条边，为避免同一条边重复计算，求解一条路径后，路径相关边的aij减1，具体过程如下(以增容单向路径子集XPE为例).

步骤1： 取出邻接矩阵上三角形得到A1.

步骤2： 将A1改为布尔矩阵，进行布尔矩阵运算，确定两点之间的连通性.

步骤4： 从A1中去除中的边，即A1中相关边对应的aij减1，得到新的邻接矩阵A1，如果新的邻接矩阵A1不为0，则转入步骤2，否则结束.

减容单向路径子集XPD={PD1,PD2,…}利用邻接矩阵下三角形通过类似步骤获得.

轮换序列路径中的每条边都代表了一次配变拆装，路径越短，拆装次数越少.由于增容边涉及供电安全性和可靠性，而减容边仅涉及到运行经济性，轮换序列路径中，增容边比减容边重要.因此，轮换序列中的路径应覆盖所有增容边,同时覆盖增容边的最短路径有利于减少拆装次数.

2.2.2环路降低借用配变容量要求 轮换过程中，环路能将增容和减容配变的互补性发挥到最大.经环路路径完成的配变轮换，既不需要新增配变，也没有配变剩余，但是需借用一台环路上任一容量的配变来配合实现轮换，避免轮换过程中因配变拆装和运输带来的停电时长.由于环路路径中借用任意节点对应容量的配变都可辅助实现轮换过程，因此，可采用扩大环路和环路嵌套来降低借用配变的要求.

图1 环路降低借用配变要求示例Fig.1 Example of reducing demand on standby transformer using loop

如图1中环路，对于4次配变增容和减容需求eab、eba、ebc和ecb而言，可以有两种环路轮换次序：第1种，路径eab→ebc→ecb→eba；第2种，路径eab→eba和路径ebc→ecb.第1种轮换次序，只需要一台借用配变，即借用va、vb和vc中任一对应容量配变就可实现4个配变的增容、减容轮换；第2种轮换序列中，需要一到两台借用配变，即借用vb和va或vb和vc对应容量的配变，才能实现4个配变的轮换.两种轮换序列都不会消耗借用配变，但扩大环路后可以减少对借用配变的需求.如图1中环路，对于6次配变增容和减容需求eab、eba、eac、eca、ebc和ecb而言，采用环路嵌套的方式形成路径eab→ebc→ecb→eba→eac→eca后，只需要节点va、vb、vc对应容量中的一台的借用配变就可完成轮换，降低了对借用配变的要求．

有向图中环路求解可以基于增容/减容单向路径.寻找XPE和XPD中，起点和终点相同的路径，形成环路子集XPR，同时将XPR中涉及路径从XPE和XPD中去除.进一步分析XPR中各路径是否存在相同节点，如有，则进一步进行环路拼接或嵌套，直至拼接或嵌套所有可拼接或嵌套的环路.

2.2.3最长路径求解 轮换序列路径中，相邻两条边表示被更换下来的配变，可被上一条边再次利用.图1中，路径eab→ebc，ebc表示配变由容量vb扩大到vc，那么被更换下的容量为vb的配变可用于eab的增容，即用容量为vb的配变替代容量为va的配变.因此单向路径中，需要增加一台该路径上容量最大的配变，会余出一台该路径上容量最小的配变.路径越长，路径中间被更换下的配变都能被充分利用.

求解最长路径集XPL时，以长度优先，寻找XPE和XPD中两条首节点和尾节点相同的可以连接的路径，拼合成更长的路径，并检查拼合路径中是否有首节点和尾节点相同点，如有，进一步拼合，如此循环拼合得到最长路径子集XPL，并将XPL中涉及路径从XPE和XPD中去除.

2.3 新增配变需求分析

有向图中，节点的一条进线表示需要一台该节点类型配变，一条出线表示有一台该节点类型的配变被置换出来.如果进线数大于出线数的数量，表示需要新增相应数量的配变来完成改造.因此，采用轮换策略对配变进行改造时，各类型配变最少需新增的数量由进线数减去出线数获得.对应到邻接矩阵A中，各节点进线减去出线的计算公式为

(2)

2.4 轮换序列优化

非环路配变轮换路径起始位置是路径尾节点相应容量的配变.环路路径起始位置是路径上任意节点对应的配变，因此，可结合新增配变或闲置配变所在位置进行选取.同时，由于环路路径不消耗配变，可以结合新增配变或闲置配变出现的时机来完成.

因减容配变改造更多的是涉及配变运行的经济性，可结合拆装、购置等成本进一步分析，将路径中不影响配变轮换次序的减容边进行取舍，以减少拆装、购置等成本.在算法求解的XPR、XPL和XPD等路径集中，分析出单向减容路径以及路径首端或末端为减容边，即形如{…,va,vb,vc,…}(a,b,c∈{1,2,…,n}，且a>b,b>c)，可根据实际情况对减容配变更换进行取舍.舍去减容边后，调整相关路径集.

3 算例

3.1 配变数据及有向图建立

本文选取江西省共青城市的配变作为分析对象，该市有四百多台配变，配变容量主要涉及8种情况，容量与有向图顶点的对应关系见表1.把过去一年存在过载/重载的配变作为增容配变；把过去一年最高负载小于10%的作为减容配变.通过查看配变监测系统，确定其中12台配变属于增容配变，6台配变属于减容配变.采用“阶梯式”配变轮换时，只考虑需增容的12台配变，其增容情况如图2(a)所示.采用“推磨式”配变轮换时，18台配变容量改造方案所形成的有向图如图2(b)所示.有向图2(b)对应的邻接矩阵A见式(3)，有向图2(a)对应的邻接矩阵A为式(3)的上三角形.通过分析有向图中存在的单向路径、环路路径和最长路径，获得“阶梯式”和“推磨式”两种方式的配变轮换序列.

表1 配变容量与有向图顶点的对应关系

图2 配变容量改造有向图Fig.2 Directed-graph of transformer capacity improvement

(3)

3.2 轮换序列求解

3.2.1“推磨式”方式 分析可达矩阵后，求解出增容/减容单向路径子集XPE和XPD,并进一步比较单向路径的起始点，优先求解环路路径子集XPR后，再求解最长路径子集XPL.将XPR和XPL，以及未被XPR和XPL合并的增容路径、减容路径合并起来形成路径集，即轮换序列X.表2给出了各路径子集和轮换序列X.在求解过程中，相同长度路径中，报废配变形成的边优先级低于可轮换配变形成的边.

因“推磨式”中增容和减容配变均参与轮换，利用有向图的邻接矩阵分析各节点进线与出线，可初步估计各类型配变新增与闲置情况，如表3所示，其中正值表示需要新增配变的数量，负值表示轮换后闲置配变的数量.采用减容路径取舍来优化轮换序列，减少配变拆装次数和配变新增/闲置数量.这里，选择对{v8,v5}减容配变不改造，去掉有向图中边e85，同时调整对应邻接矩阵后，可得减容路径取舍后配变新增数量，如表3所示.

减容路径取舍过程后，修正后轮换序列X中包含路径见表4.此时，需新增1台v4和3台v5节点对应配变，利用v4和v5对应配变可启动配变轮换，X中涉及17条边，共需拆装配变17次.可优先利用新增的v4容量配变完成环路路径{v2,v4,v6,v4,v2}，然后利用置换出来的v4容量配变完成非环路路径{v1,v2,v4,v5,v7,v4}.轮换结束后，消耗1台v4和3台v5型号的配变，多出1台v1和1台v2型号的配变.

表2 “推磨式”方法路径集分析

表3 “推磨式”方法配变新增数量

3.2.2“阶梯式”方式 采用“阶梯式”配变轮换方式，只对增容配变进行，因此取有向图邻接矩阵的上三角形，增容单向路径子集XPE即为所求解的轮换序列X，其中路径及其起始位置选择见表5.此时，需要v7、v6和v5型号的配变各2台发起配变轮换，共需拆装12次配变.新增的6台配变将全被消耗，轮换结束后闲置1台v1、2台v2和1台v3型号的配变.

表4 “推磨式”轮换序列路径分析

表5 “阶梯式”轮换序列路径分析

4 总结

针对目前配变轮换多是根据配变改造的迫切度和已更换下来的配变进行调配，缺乏统一的规划和管理.本文基于有向图提出了一种配变轮换需求的表达模型，通过有向图连通路径的分析，易于结合“阶梯式”、“推磨式”经验确定配变轮换次序.由于文中直接将容量大小视为型号，而实际配变改造中，配变型号除了容量大小，还涉及损耗、干式、油浸式等选择，可根据用户负荷特性，在容量选择时兼顾配变其他性能，提高方法的适用性.

参考文献：

[1] 李亦言，严正，冯冬涵．考虑城市化因素的中长期负荷预测模型[J]．电力自动化设备，2016，36(4)： 54-61．

[2] 罗勇，李芳．基于负荷预测的电力市场寡头竞争分析[J]．郑州大学学报(理学版)，2013，45(3)：110-114．

[3] 刘晓慧，伍斌．农网改造中10 kV配电变压器的选用及安装[J]．江西电力，2012，36(1)：201．

[4] BICEN Y, ARAS F, KIRKICI H．Lifetime estimation and monitoring of power transformer considering annual load factors[J]．IEEE transactions on dielectrics and electrical insulation, 2014, 21(3): 1360-1367．

[5] HU Y，DONG F，WANG X．The optimization study of asset retirement and reuse management in electric power enterprises[C]//China International Conference on Electricity Distribution．New York， 2012：1-5．

[6] 穆广平．基于资产全寿命的技改辅助决策及再利用管理[J]．电力与能源，2014，35(1)：113-116．

[7] 滕开萱．变压器“辞旧迎新”村民放心过春节[J]．广西电业，2015(Z1)：35．

[8] 俞玉英，郭铭，郭寅昌，等．配电网建设改造工程评价方法[J]．电力系统及其自动化学报，2012，24(5)：123-126．

[9] LAURITZEN S L，SPIEGELHALTER D J．Local computations with probabilities on graphical structures and their application to expert systems[J]．Journal of the royal statistical society(Series B methodological)，1988：157-224．

[10] 岳昆，刘惟一，李维华，等．基于语义的Web服务行为建模方法[J]．郑州大学学报(理学版)，2007，39(4)：126-129．

[11] YANG S，TAN S，XU J X．Consensus based approach for economic dispatch problem in a smart grid[J]．IEEE transactions on power systems，2013，28(4)：4416-4426．

[12] RODRIGUEZ R A，BECKER S，ANDRESEN G B，et al．Transmission needs across a fully renewable European power system[J]．Renewable energy，2014，63：467-476．

[13] 侯成滨，王瑞峰．基于最小生成树的含分布式电源的配电网重构算法[J]．郑州大学学报(理学版)，2016， 48(4)：102-108．