基于感应磁场的潜艇磁异常计算模型
刘 辉
基于感应磁场的潜艇磁异常计算模型
刘 辉
(中国船舶重工集团公司 昆明船舶设备研究试验中心, 云南 昆明, 650051)
由地磁感应引起的潜艇磁异常是现代航空反潜的重要依据, 研究磁异常对潜艇防护有重要意义, 文中针对潜艇感应磁异常缺乏完整计算模型的现状, 采用磁体模拟法将潜艇感应磁矩看作3个正交磁偶极矩的叠加, 并根据潜艇椭球体模型在外场中的磁化规律, 推导了感应磁矩的解析表达式, 进而得到磁异常计算公式。最后通过仿真, 得到潜艇感应磁异常在高空的分布特性, 仿真结果符合实际情况, 基本印证了计算模型的正确性。
航空反潜; 潜艇; 磁异常; 磁偶极子; 感应磁场
0 引言
潜艇由钢铁建造而成, 是一个大型铁磁体, 由于长期处在地磁场的磁化作用下, 产生了固定磁矩与感应磁矩[1]。固定磁矩可以看作固定值, 不会随着海域地磁场值与潜艇航向的变化而改变, 感应磁矩和海域地磁场值与潜艇航向关系密切, 且很难通过消磁手段消除, 是潜艇磁矩的重要构成, 由感应磁矩引起的磁异常是当前航空反潜的重要依据, 文中针对潜艇感应磁性形成的磁异常进行研究。
当前对潜艇磁异常的研究主要集中于建模方法以及探测技术[2-5], 普遍采用的建模方法有积分方程法、有限元法以及磁体模拟法等[6]。积分方程法有严格的理论依据, 需要对潜艇磁矩构成进行精确的剖分, 建模过程抽象, 数学模型复杂且计算量大, 结果不够直观。有限元法可借助计算机辅助软件(ANSYS、Flux等)建立高精度的潜艇几何模型, 并划分有限元网格得到单元区域, 再进行数值求解, 将潜艇磁场建模问题转化成泛函变分问题, 可以得到潜艇磁场的有限元数值解。但由于潜艇体积大, 需要建立庞大的潜艇、海水以及空气的网格模型, 计算量很大, 普通计算机无法完成。该方法可用于仿真分析潜艇局部的精细特性, 在分析潜艇高空的磁异常时不便使用。磁体模拟法又称等效源法, 利用已知磁场分布的磁性物体来等效实际潜艇, 模拟潜艇磁场, 其建立模型过程较为简单, 磁场数学模型通常计算量小且直观易懂, 虽然在分析潜艇近场时误差较大, 但在远场条件下较为准确, 用于分析潜艇高空的磁异常较为适用。上述不同方法建模的原理和思路不同, 但得到的结论基本一致。
参考文献[2]与[3]将潜艇磁矩等价于某个方向上的磁偶极矩来推算潜艇磁场, 但只推导了潜艇磁异常与潜艇磁矩之间的函数关系, 并未给出潜艇磁矩的详细计算方法。文中在前人研究的基础上[7-8], 针对潜艇感应磁异常缺乏完整计算模型的现状, 采用磁体模拟法, 将潜艇看作旋转椭球体模型, 在高空探潜的情况下, 分解潜艇感应磁矩为3个方向正交的磁偶极矩, 并依据椭球体模型在外磁场中的磁化规律, 推导潜艇感应磁矩作为潜艇尺寸、航向以及地磁场强度等参数变量的函数表达式, 最终达到计算磁异常的目的。
1 磁偶极子模型
磁偶极子是最基本的磁单元, 在磁场分析中有着重要的作用, 自然界的任何磁矩都可以认为是若干个磁偶极矩的叠加, 对于磁偶极子的磁场, 计算方法有很多, 但大多数是在极坐标下的计算结果, 文中需要计算磁场在高空平面上的分布, 因此选择一种直角坐标系下的磁偶极子磁场计算方法。
如图1所示, 以偶极子模型的中心为坐标原点, 海平面为平面, 垂直于海平面向上为轴方向, 建立右手直角坐标系, 对于空间中的任意一点(,,), 偶极子在该点产生的磁感应强度可表示如下。
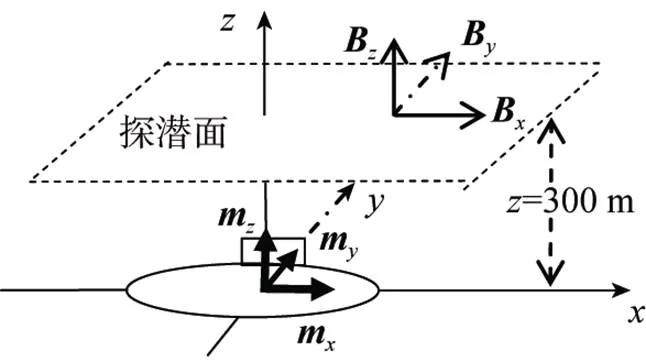
图1 计算模型坐标系
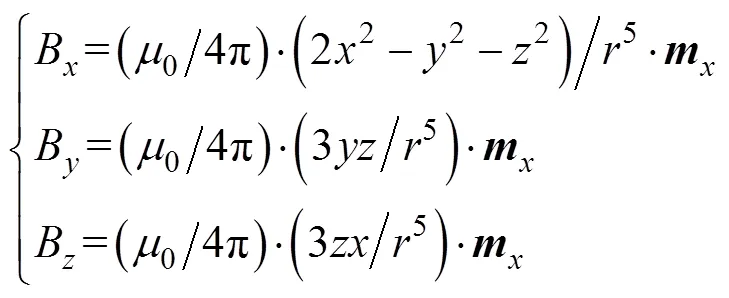
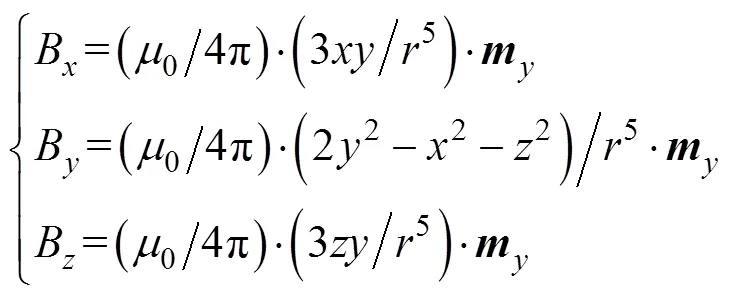

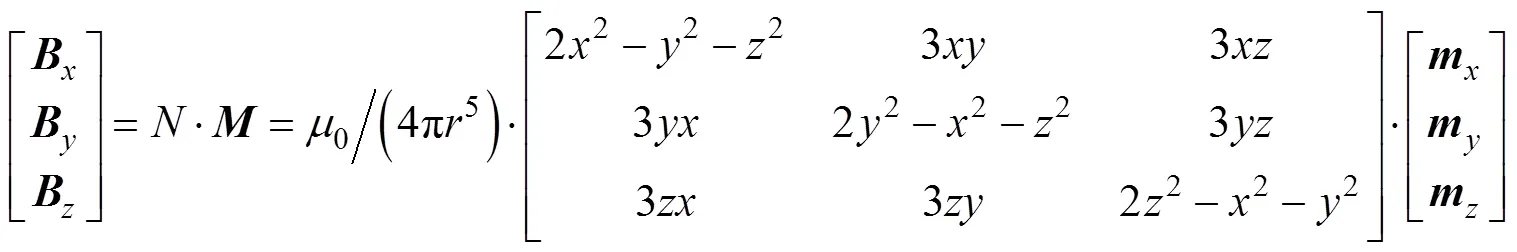
若能通过计算或者测量得到潜艇在3个方向上的磁矩、、的值, 便可利用上式来计算潜艇在周围空间任意一点的磁场值。
2 潜艇感应磁矩
潜艇在出航前需经过消磁, 以减小被发现或者被攻击的概率, 消磁后的潜艇, 固定磁矩对潜艇磁矩的贡献很小; 但由地磁场磁化引起的感应磁矩, 无法通过简单的消磁方式去除, 成为潜艇磁矩的最主要贡献部分, 因此文中的研究重点则放在潜艇感应磁矩上, 在地磁场的磁化作用下, 潜艇3个方向上的感应磁矩不但与潜艇的尺寸、材料等诸多因素有关, 而且与潜艇所在海域的地磁场值、方向以及潜艇航向有着重要关系[9]。由于潜艇感应磁矩是由地磁场磁化引起的, 所以与地磁场之间有着固定的关系, 潜艇形状近似于旋转椭球体, 在远场计算条件下, 可将潜艇看作旋转椭球体模型, 根据椭球体模型在外场中的磁化规律, 潜艇磁矩三分量同地磁场三分量之间的函数关系可表示为[10]
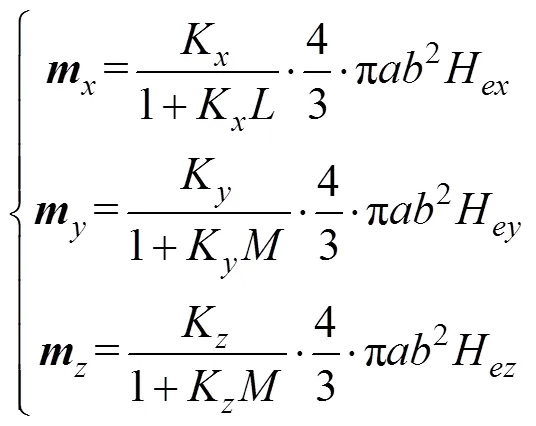
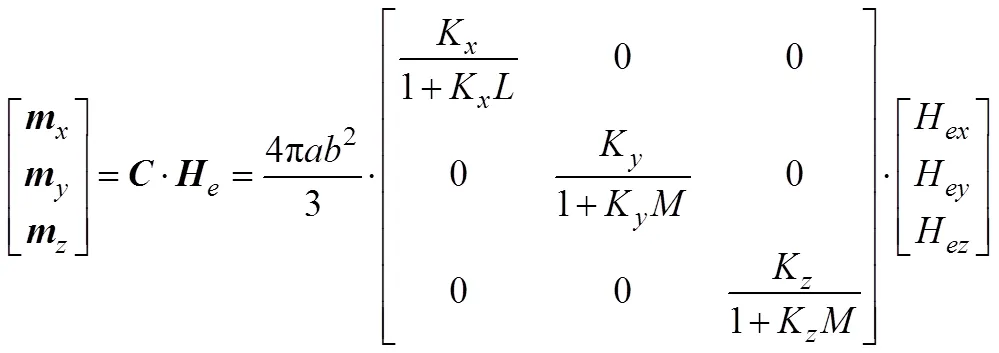
其中:为系数矩阵;K、K、K为舰艇在3个方向上的等效磁化率, 与舰艇的材料、质量以及体积尺寸相关;和分别为舰艇长轴与短轴方向上的去磁系数, 在将潜艇看作旋转椭球体模型时,和可以通过式(7)计算得到[11]


表1 椭球体退磁因子
选择正确的潜艇尺寸与材料参数, 根据式(7)可以算出系数矩阵, 再乘以潜艇长、宽、高3个方向上的地磁场值, 即可计算得到潜艇在3个方向上的磁矩值。但由于式(6)描述的磁矩计算公式中, 所需地磁场值是潜艇坐标系下的, 所以需先将地理坐标系下的地磁场值转换到潜艇坐标系下, 如图2所示。
潜艇磁场在潜艇坐标系与地理坐标系之间的变换关系为

式中:为变换矩阵;H表示地磁场值, 下标、、为地理坐标系,、、为潜艇坐标系。
从以上推导可以看出, 在潜艇尺寸和材料等参数确定了的情况下, 其3个方向上的磁矩即可由所处海域的地磁场H以及航向角完全确定。
由于文中所要计算的是潜艇在地理坐标系下的磁场, 因此需要将在潜艇坐标系下的计算结果再变换到地理坐标系下, 最终可得到三轴偶极子在地理坐标系下产生的磁感应强度为

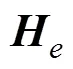
3 感应磁矩形成的磁异常
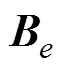

为了仿真潜艇磁异常的分布, 并对比不同海域与航向下潜艇磁异常的差别, 设潜艇分别处于在高纬度海域与低纬度海域航行的2种情况, 2种海域的地磁场值如表2所示。
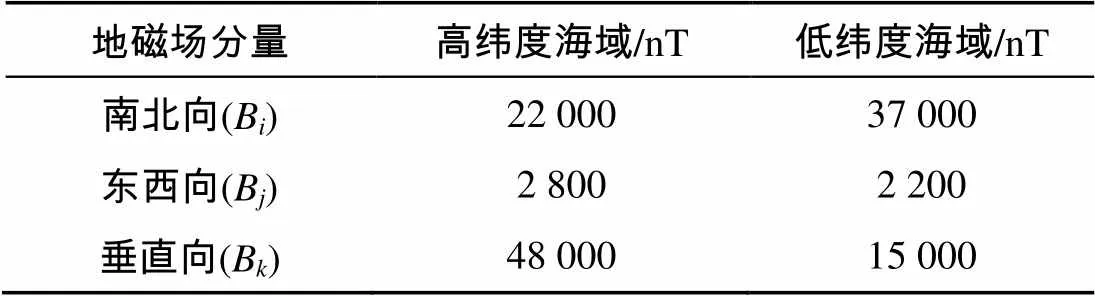
表2 不同海域的地磁场强度
反潜机所探测到的潜艇磁异常只与潜艇和反潜机之间的相对位置有关, 与潜艇航行深度无直接关系。假设潜艇的固有磁性已完全消除, 只考虑潜艇的感应磁性在探潜平面上形成的磁异常, 取反潜飞机距潜艇的飞行高度为300 m, 采用MATLAB仿真潜艇上方=300 m的平面上,、方向为±1 000 m范围内, 高低2种海域位置, 南北、东西2种航向, 共4种条件下反潜飞机所探测到的潜艇磁异常强度分布, 结果如图3~6所示。
通过仿真结果可得出结论如下。
1) 潜艇感应磁异常在300 m高空处的强度值约为0.3~2 nT, 分布特性为典型的磁偶极子场。
2) 对于特定的潜艇, 南北向航行时的磁异常强度要大于东西向航行时, 因为潜艇在长度方向的退磁因子要远小于宽度方向, 在外场下更容易磁化。因此潜艇在被反潜机搜索时, 应调整为东西向航行, 可降低被发现的概率。
3) 航向对潜艇感应磁异常有重要的影响, 但在高纬度海域表现的不如低纬度海域明显。因为高纬度海域地磁场垂直分量大, 而垂直分量引起的感应磁场与航向无关。
以上仿真结果得出的结论, 都与实际情况相符, 且仿真结果的量值与文献[13]采用的有限元法得到的值基本相同, 其分布特性与文献[14]记载的一致, 基本印证了文中所建立的潜艇感应磁异常计算模型的正确性。
4 结束语
利用潜艇形状类似于旋转椭球体的特点, 在文中将潜艇磁矩分解为3个方向正交的磁偶极矩, 依据椭球体模型在外场中的磁化规律, 由潜艇的尺寸、形状等参数以及地磁场值推导出潜艇磁矩的计算公式, 并根据反潜飞机磁探仪的探测原理, 得到潜艇的磁异常计算模型, 可较为精确地计算潜艇感应磁异常。最后对所建立的计算模型进行了软件仿真, 仿真结果与实际情况基本符合, 表明文中所建立的数学模型的正确性。
文中只针对潜艇的感应磁性引起的磁异常做了一些基础性研究, 后续还需结合潜艇固定磁性与感应磁性对潜艇磁异常进行全面的研究, 再根据当前航空磁探的实际情况, 对潜艇磁异常的精细特性做进一步研究。
[1] 义井胤景. 磁工学[M]. 胡超, 译. 北京:国防工业出版社, 1977.
[2] 张朝阳, 虞伟乔. 基于磁偶极子等效的潜艇空间磁场分布[J]. 舰船科学技术, 2013, 35(1): 31-34.
Zhang Chao-yang, Yu Wei-qiao. Research on Spatial Magnetic Field Distributing of Submarine Based on Magnetic Dipole Equivalent[J]. Ship Science and Technology, 2013, 35(1): 31-34.
[3] 王珺琳, 刘金荣, 吕政良, 等. 基于空间磁场模型的航空磁探测分析方法[J]. 中国电子科学研究院学报, 2016, 11(1): 32-35.
Wang Jun-lin, Liu Jin-rong, Lü Zheng-liang, et al. The Aeromagnetic Exploration Analysis Method Based on Spatial Magnetic Field Model[J]. Journal of China Academy of Electronics and Information Technology, 2016, 11(1): 32-35.
[4] 伍东凌, 石超, 王秀. 潜艇磁异常信号与方位对应关系的研究[J]. 舰船电子工程, 2012, 32(9): 56-58.
Wu Dong-ling, Shi Chao, Wang Xiu. Study of Relationship between Magnetic Anomaly Signal and Location Information of the Submarine[J]. Ship Electronic Engineering, 2012, 32(9): 56-58.
[5] 单志超, 曲晓慧, 杨日杰, 等. 潜艇航向对直升机磁异探潜的影响[J]. 火力与指挥控制, 2013, 38(2): 62-68.
Shan Zhi-chao, Qu Xiao-hui, Yang Ri-jie, et al. Research on Effect of Helicopter Magnetic Anomaly Detecting Submarine from Change of Submarine Heading[J]. Fire Control & Command Control, 2013, 38(2): 62-68.
[6] 周家新, 陈建勇, 单志超, 等. 航空磁探中潜艇磁场建模方法分析[J]. 海军航空工程学院学报, 2017, 32(1): 143-148.
Zhou Jia-xin, Chen Jian-yong, Shan Zhi-chao, et al. Analysis of Submarine Magnetic Field Modeling Method for Aero Magnetic Detection[J]. Journal of Naval Aeronautical and Astronautical University, 2017, 32(1): 143-148.
[7] 张昌达. 关于磁异常探测的若干问题[J]. 工程地球物理学报, 2007, 4(6): 550-551.
Zhang Chang-da. Some Problems Concerning the Magnetic Anomaly Detection(MAD)[J]. Chinese Journal of Engineering Geophysics, 2007, 4(6): 550-551.
[8] Nan Zan, Arye Nehorai. Detection of Ship Wakes Using an Airborne Magnetic Transducer[J]. IEEE Transactions on Geoscience and Remote Sensing, 2000, 38(1): 532-538.
[9] 叶平贤, 龚沈光. 舰船物理场[M]. 北京: 兵器工业出版社, 1992.
[10] 周耀忠, 张国友. 舰船磁场分析计算[M]. 北京: 国防工业出版社, 2004.
[11] 赵凯华, 陈熙谋. 电磁学[M]. 北京: 高等教育出版社, 1985.
[12] 张昌达. 量子磁力仪研究和开发近况[J]. 物探和化探, 2005, 29(6): 283-287.
Zhang Chang-da. Recent Advances in the Research and Development of Quantum Magnetometers[J]. Geophysical and Geochemical Exploration, 2005, 29(6): 283-287.
[13] 吴芳, 吴铭, 杨日杰, 等. 反潜巡逻机运动态势对潜艇磁异常信号的影响分析[J]. 测试技术学报, 2017, 31(4): 283-289.
Wu Fang, Wu Ming, Yang Ri-jie, et al. Analysis the Affection of the Anti-Submarine Aircraft’s Movement Situation to the Magnetic Anomaly Signal of Submarine[J]. Journal of Test and Measurement Technology, 2017, 31(4): 283-289.
[14] 崔凯兴. 潜艇标量磁场在探潜平面上的分布研究[J]. 科技广场, 2014(12): 15-18.
Cui Kai-xing. Research on the Distribution of Submarine Scalar Field in Anti-Submarine Plane[J]. Science Mosaic, 2014(12): 15-18.
(责任编辑: 许 妍)
Magnetic Anomaly Calculation Model of Submarine Based on Induced Magnetic Field
LIU Hui
(Kunming Shipborne Equipment and Test Center, China Shipbuilding Industry Corporation, Kunming 650051, China)
The magnetic anomaly of a submarine caused by geomagnetic induction is an important evidence for modern airborne anti-submarine measure. It is of great significance to study the magnetic anomaly for submarine protection. In view of the present situation that there isn't complete calculation model for submarine induced magnetic anomaly, this paper regards the induced magnetic moment of submarine as the superposition of three orthogonal magnetic dipole moments by means of magnet simulation. According to the magnetization law of the ellipsoid model of a submarine in outfield, the magnetic moment expression of a submarine is derived, and then, the computational formula of submarine magnetic anomaly is obtained. Further, the simulation is performed to achieve the induced magnetic anomaly strength distribution of a submarine at high attitude area, and the result conforms to the actual situation, which verifies the correctness of the proposed calculation model.
airborne anti-submarine; submarine; magnetic anomaly; magnetic dipole; induced magnetic field
TJ67; O484.52; U665.18
A
2096-3920(2018)02-0152-05
10.11993/j.issn.2096-3920.2018.02.009
刘辉. 基于感应磁场的潜艇磁异常计算模型[J]. 水下无人系统学报, 2018, 26(2): 152-160.
2018-01-05;
2018-02-01.
刘 辉(1987-), 男, 工程师, 主要研究方向为目标磁特性模拟技术

