刍议小升初数学应用问题有效衔接
闫岚子
(西藏拉萨市江苏中学 850000)
一、和、差、倍、商、积问题
1.和、差问题
(1)和
求两个或两个以上数的和,用加法.
(2)差(多少的问题)
①求两个量的差是多少
求两个数的差,用减法, 用较大的数减去较小的数.
②已知甲数,乙数比甲数多(或少)多少,求乙数
甲数是a,乙数比甲数的多(或少)b,则乙数是a+b或a-b.
2.倍数、商、乘积
(1)求一个数是另一个数的多少倍,用除法
(2)已知两个因数的积与其中一个因数,求另一个因数,用除法
(3)求一个数的几倍是多少
例1 一个数是12,另一个数是这个数的n倍,求另一个数.
解析12n.
例2 甲数是a,乙数比甲数的2倍多(或少)3,乙数是多少?
解析2a+3或2a-3.
归纳求一个数的几倍是多少,用乘法.
二、分数(百分数)、归一问题
1.分数(百分数)
(1)求一个数的几分之几(或百分之几)
例已知一个数是a,求这个数的四分之一(或25%)是多少?
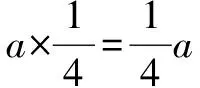
归纳求一个的几分之几(或百分之几),用乘法.
(2)求一个数是另一个数的几分之几(或百分之几).
例一个数是25,另一个数是125,求25是125的几分之几(百分之几).
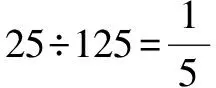
归纳求一个数是另一个数的几分之几(或百分之几),用除法.
(3)已知一个数的几分之几(或百分之几)是多少,求这个数.
例一个数的五分之一是25,求这个数.
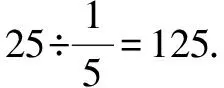
归纳已知一个数的几分之几(或百分之几)是多少,求这个数,用除法.
(4)求一个数比另一个数多(或少)百分之几
例15比12多百分之几?12比15少百分之几?
解析(15-12)÷12=0.25=25%.
(15-12)÷15=0.2=20%.
归纳求一个数比另一个数多(或少)百分之几,用两数的差除以“比”字后面的数即可.
(5)已知一个数增加了百分之几,求增加(或减少)了多少; 增加(或减少)到多少?
例1 某市城镇人口14万,农村人口28万,计划一年后城镇人口增加0.8%,农村人口增加1.1%.则:
计划一年后城镇人口增加____万;
计划一年后农村人口增加____万;
计划一年后城镇人口增加到____万;
计划一年后农村人口增加到____万.
解析计划一年后城镇人口增加了:14×0.8%=0.112万;
计划一年后农村人口增加了:28×1.1%=0.308万;
计划一年后城镇人口增加到:14+14×0.8%=14(1+0.8%)=14.112万;
计划一年后农村人口增加到:28+28×1.1%=28(1+1.1%)=28.308万.
归纳求增加了多少就是求一个数的百分之几,用乘法.
求增加到多少即增加后达到多少就是求一个数与增加的量的和= 一个数×(1+a%).
例2 一批钢材200吨,运走了80%,还剩多少吨?
解析剩余的百分数:1-80%=20%,
剩余的钢材量:200×20%=40.
综合列式:200×(1-80%)=200×20%=40吨.
归纳把开始的量看成单位“1”,给“1”加上(减去)增加(减少)的百分数算出增加(减少)后的百分数,再给结果乘以开始的量即为增加(或减少)后的量.
当开始(原来)的量为m,增加(或减少)a%,则增加(或减少)后的量为m(1+a%) 或m(1-a%).
训练学生运用单位“1”参与运算,熟练运用(1±a%),为后面初中代数式的学习做好准备.
2.归一问题
(1)单一量
例2台同样的抽水机,3小时可以浇地1.2公顷,照这样计算,一台抽水机每小时可以浇地多少公顷?
解析1.2÷2÷3=0.2(公顷).
答:一台抽水机每小时可以浇地0.2公顷.
归纳单一量(1份数量)=总数÷份数.
(2)归一问题
例3台拖拉机3天耕地90公顷,照这样计算,5台拖拉机6 天耕地多少公顷?
解析1台拖拉机1天耕地多少公顷?90÷3÷3=10(公顷).
5台拖拉机6天耕地多少公顷? 10×5×6=300(公顷)
综合算式 90÷3÷3×5×6=10×30=300(公顷).
答:5台拖拉机6 天耕地300公顷.
归纳先求单一量,以单一量为标准,求出所要求的数量.
三、行程问题
1.相遇问题
例甲乙两车从两地同时出发相向而行,甲车每小时行40千米,乙车每小时行60千米,经过3小时相遇.两地相距多少千米?
解析甲乙同时出发直到相遇所用时间相等都是3小时,
40×3+60×3=300(千米).
答:两地相距300千米.
归纳总路程=甲的速度×相遇时间+乙的速度×相遇时间.
同时出发直到相遇的时间称为相遇时间,甲乙两个运动物体所用的时间相等.
2.追及问题
例1 跑得快的马每天走240里,跑得慢的马每天走150里,慢马先走12天,慢马先走了多少里?快马20天时间可以追上慢马,快马追上慢马走了多少里,慢马被追赶过程走了多少里?(1里=0.5千米)
解析慢马先走的路程:150×12=1800(里),
快马追赶慢马走的路程:240×20=4800(里),
慢马被追赶过程走的路程:150×20=3000(里).
归纳追赶的路程 =追赶者的速度×追及时间.
被追赶的路程=被追赶者的速度×追及时间.
路程=各自的速度×追及时间.
注:追赶和被追赶过程用的时间相同,统称为追及时间.
3.水流问题、逆风顺风问题
例一艘客轮在静水中的速度是24km/h,水流的速度是3km/h,客轮顺水航行的速度是多少?逆水航行速度是多少?
解析客轮顺水航行的速度:24+3=27(km/h),
客船逆水航行的速度:24-3=21(km/h).
答:客轮顺水航行的速度是27km/h,逆水航行速度是21 km/h.
归纳轮船在顺水中的速度=轮船在静水中的速度+水流速度,
轮船在逆水中的速度=轮船在静水中的速度-水流的速度.
同理,飞机顺风速度=飞机在无风时的速度+风速,
飞机逆风速度=飞机在无风时的速度-风速.
四、工程问题
例一件工程,甲队单独完成需100天,乙队单独完成需150天.甲乙两队合作50天后,剩下工程由乙队单独完成还需要多少天?
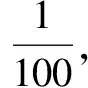


剩下的工作量=1-合作m天的工作量.
乙单独完成剩下工作量所用时间=剩余工作量÷乙的工作效率.
结束语:以上为初中数学学习必须要掌握的几类小学数学问题模型.实践证明通过在小升初初期的专项训练,尤其是对原来应用问题掌握不好的学生效果显现.
参考文献:
[1]吴渊. 关于初中数学教师对“中小衔接问题”认识的调查研究[D].沈阳:沈阳师范大学, 2013.
[2]游小云. 小升初衔接的数学教学策略[J]. 中小学数学, 2015(3): 18-19.
[3]赵志鹏. 探究小升初衔接教学中数学学困生的转化策略[J], 数理化学习: 教育理论版, 2013(10): 13-13.
[4] 许康华. 初中预备班·小升初衔接教材数学[M]. 杭州:浙江大学出版社, 2013.
[5]吴志文,试析做好“升初”衔接教学—兼谈高效数学课堂教学的构建[J], 考试周刊, 2016(10): 255.
[6]薛莉. 刍议“小升初”数学衔接[J]. 数学教学, 2017(11): 64.

