识图、标图、研图——从图形教学谈几何学习的有效性

孙金勇

(浙江省温岭市石塘镇中学 317500)

一、识图

识图既是要把图形语言转化为符号语言或文字语言，也要能够根据符号语言或文字语言精确的画出图形.而识图能力是初中阶段培训学生几何能力以及空间想象能力的的基础，需要教师在平时的几何课堂上通过不断的锻炼而达到强化.

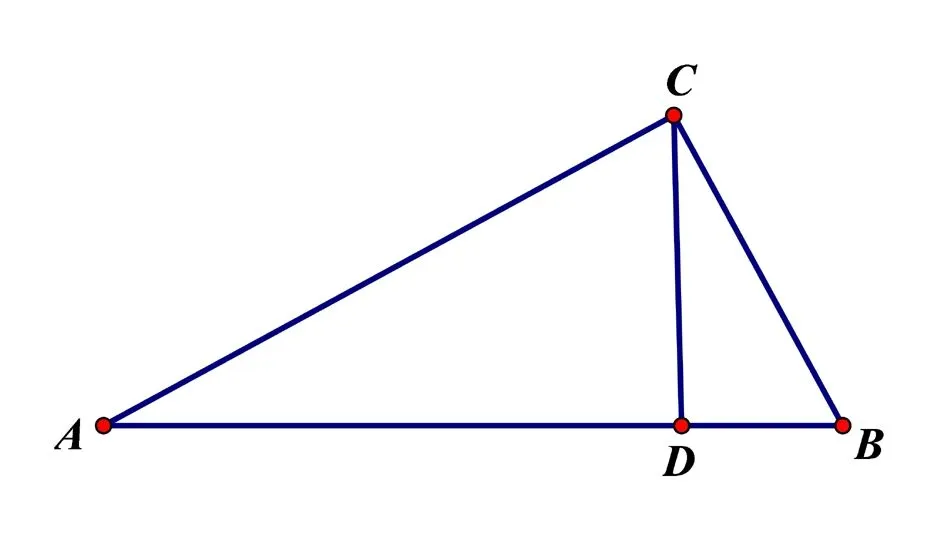
(2)求∠ACB的大小.

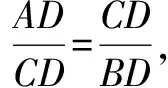
分析(2) 对于第二问，可以这样设计问题，∠ACB大家觉得这个角会是多少度？学生会回答90°，那么怎么得出这个∠ACB是直角呢？在这个图形中除了直角有哪些角是相等的，为什么？学生会回答通过刚才(1)小题两三角形相似来得出.

二、标图

标图是几何图形在审题的同时，把已知条件尽量都标在图形中，把符号语言，文字语言体现在图形中.然后在分析的时候在图形上进行统筹思考，有利于整体把握一道题目，培养学生的几何分析能力和合情推理能力.

例2 如图，△ABC中，AB+AC=6cm，BC的垂直平分线l与AC相交于点D，则△ABD的周长为____cm.

分析这道题分析时这样引导学生思考，BC的垂直平分线l与AC相交于点D，这个条件可以得出什么？学生回答垂直、平分的都有，最主要的应该得出BD=CD，同时在图中及时用短竖线标出BD=CD，这样所求的△ABD的周长就转化为AB+AD+BD即AB+AC的长度，就可以得出答案6cm.

对于题目中相等的一组线段用一个短竖表示，对于第二组相等的线段可以用两个短竖.类似的对于相等的一对角用一个短弧线表示，对于第二组相等的角可以用两个短弧线表示，以此类推.

如果平时教师重视学生画图能力的培养，对学生利用图形解决问题的能力将会得到提高.有时候画出标准的图形，清晰的图形会使解题的思路得到涌现，或者有时候就可以直接从规范的图形中得到答案.

三、研图

几何基本图形始终贯穿于整个主题或模块，几何基本图形把每节课进行衔接，往往一节课就有一个基本图形.比如角平分线、垂直平分线等，这些基本图形对系统的学习几何主题、模块起到串联作用.能把知识串点成线、织线成网、沟通知识间的联系，能突出数学知识的系统性，彰显重点难点，梳理逻辑顺序.

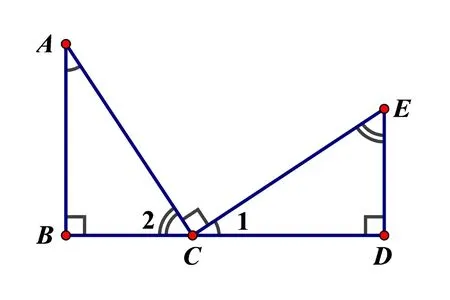
例3 在Rt△CAB和Rt△ECD中，AC=CE，点D在边BC的延长线上，且∠ACE= ∠B=∠D=90° ，你能得出哪些结论？

分析一对斜边对应相等，∠B=∠D=90°，通过∠ACE=90°可以得出∠A=∠1，∠2=∠E，两个直角三角形△CAB≌△ECD，AB=CD，BC=DE.

变式：在直线l上依次摆放着七个正方形(如图所示).已知斜放置的三个正方形的面积分别是1、2、3，正放置的四个正方形的面积依次是S1、S2、S3、S4，则S1+S2+S3+S4=____.

分析本图中包含上述的基本图形，S1、S2和斜放面积是1的正方形组成基本图形，由勾股定理结合基本图形得出S1+S2=1；S3和S4和斜放面积是3的正方形组成基本图形，得出S3+S4=3，∴答案=4.

综述，只要教师能在平时课堂上关注学生学习几何时的状态，让学生动起手来，让学生参与进来，那么这样学生在课堂上学习几何的积极性将大大加强，这样就能进一步提高几何学习的有效性，有利于学生几何能力的培养.

参考文献：

[1]王兄.基于图式的数学学习研究[D].上海：上海华东师范大学,2004.

[2]席高文，许梦日.中学几何研究与教学[M].郑州：郑州大学出版社,2007:174.

[3]李秋丽.变式教学在初中数学教学中的应用[D].武汉：华中师范大学,2013:15-20.