垂径定理牵手勾股定理

谢 勇 唐雪锋

(湖北省枣阳市兴隆一中 441218)

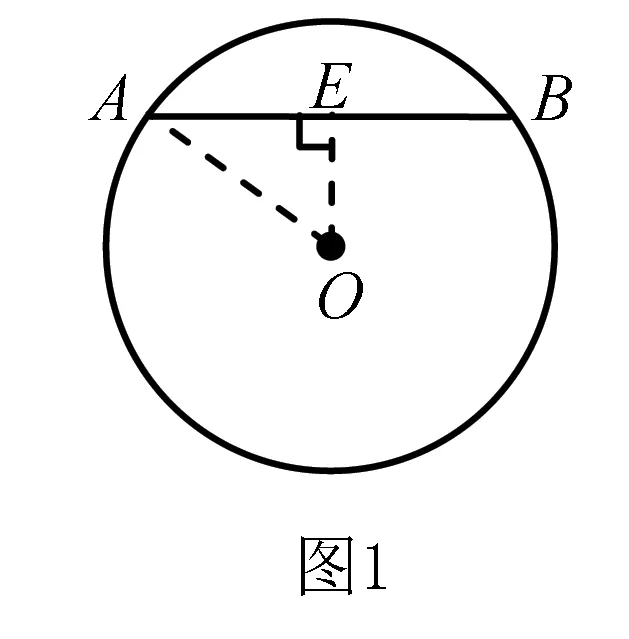
典例(人教版数学教材九年级上册第83页练习第1题)如图1，在⊙O中，弦AB的长为8 cm，圆心O到AB的距离为3 cm．求⊙O的半径．

解过点O作OE⊥AB，E为垂足，连接OA．

在Rt△AEO中，∵OE2+AE2=OA2，

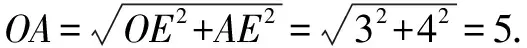
∴⊙O的半径为5 cm．

规律解题过程中涉及垂径定理和勾股定理．在图1中，OA是半径，我们把OE叫做弦心距(即圆心到弦的距离)，AE叫做半弦，求解与垂径定理相关的圆类计算问题时，通常需要把相关数量集中到由它们所组成的直角三角形中，运用勾股定理解决．

思考1 将条件与结论互换位置思考．如图2，⊙O的半径为5 cm，CD为直径，弦AB⊥CD于点E，OE=3 cm，求弦AB的长．

点评典例是已知半弦、弦心距，求圆的半径问题，而本题是已知半径、弦心距，求半弦的问题．探究几何问题的一种常用方法就是象这样，将已知条件与结论互换位置思考．另外，比较图1和图2，发现在解决有关弦的问题时，往往只需从圆心作一条与弦垂直的线段即可．

思考2 变换条件思考．如图3，在⊙O中，弦AB的长为8 cm，点C在⊙O上，且OC⊥AB，垂足为点E，若CE=2 cm，求⊙O的半径．

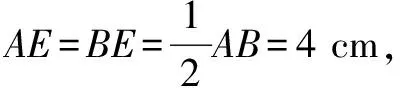
点评和典例相比，它们均是在同一个直角三角形中运用勾股定理计算求解．所不同的是，本题构建的是弦长、半径、弦心距等数量间的方程模型，这和课本第82页的例题解法是一样的．

思考3 将静止图形动态化思考．如图4，⊙O的直径为10 cm，弦AB的长为8 cm，E是弦AB上的一个动点，那么OE的长的取值范围是____．

分析求OE的长的取值范围，实际上就是找OE的最大值和最小值，弦上的点与圆心的距离的最大值就是该圆的半径，而最小值是弦心距．

点评动态化思考图形，可多取几个点E，并将它与圆心连接起来，比较后，会发现其中蕴含着垂线段最短的数学道理．

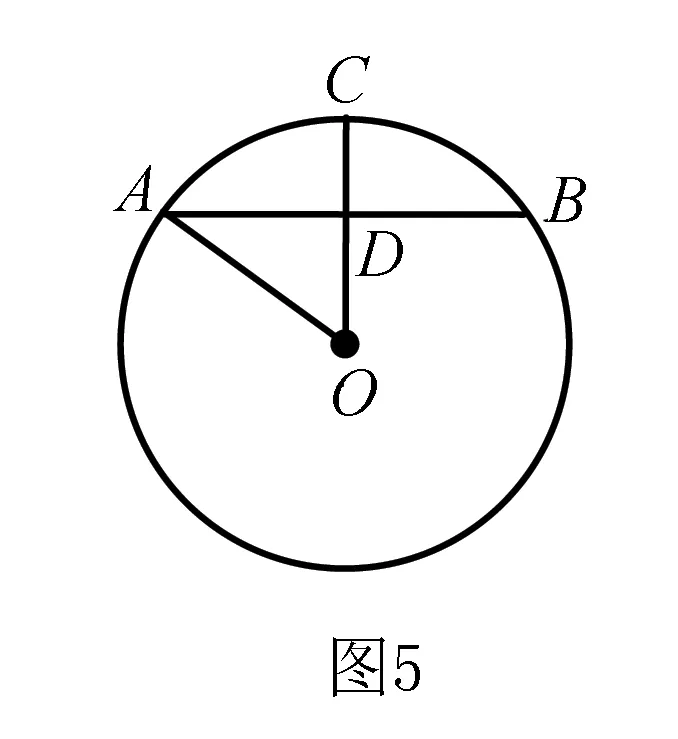
小结如图5，在⊙O中，OC⊥AB于点D，AB=l，OA=R，OD=d，CD=h，根据OA2=AD2+OD2及OC=OD+CD，当知道l、R、d、h中的任意两个量时，就可以求出剩余的两个量．

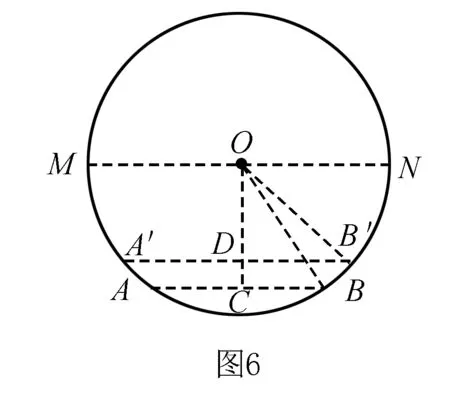
拓广探索如图6，在圆柱形油槽内装有一些油，截面如图，油面宽AB为6分米，如果再注入一些油后，油面AB上升1分米，油面宽变为8分米，圆柱形油槽直径MN为____分米．

解取油面AB上升1分米到达A′B′的位置，过点O作OC⊥AB于点C，交A′B′于点D，连接OB，OB′．

∴AB=6，A′B′=8，CD=1．

由勾股定理，得OB2=OC2+CB2，OB′2=OD2+DB′2．

而OB=OB′，OC=OD+CD=OD+1，

∴(OD+1)2+32=OD2+42，解得OD=3．

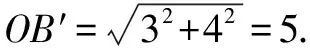
∴MN=2OB′=10(分米)．

故答案填10．

点评这是一道与圆有关的实际应用题，求解关键是从中构建如典例1那样的基本图形，综合运用垂径定理和勾股定理构建方程求解．

参考文献：

[1]姜晓翔．基于“自主变式” 引发“生本探究”[J]．中国数学教育(初中版)，2016(10)：15-17．