浅谈初中数学教学中的“变式”教学
张海能
(福建省三明市梅列区第一实验学校 365000)
过去教师在教学中,多注意概念等知识的理解和记忆,在其运用上做得不够.因此,学生解决实际问题时,往往由于概念不清而导致错误,所以教师在吃透教材的基础上,通过“变式”引导学生从多方面思考,拓宽学生的思路,提高学生的应变能力.
一、通过对定理公式的“变式”,提高学生解题的技巧性

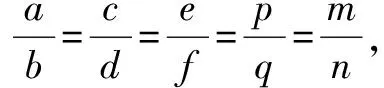
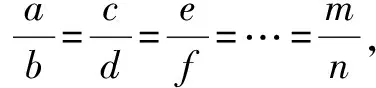

在练习和应用中,若能恰当运用“变式”,可使解题来得巧妙简捷.
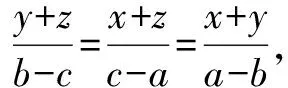
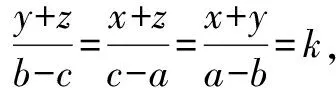
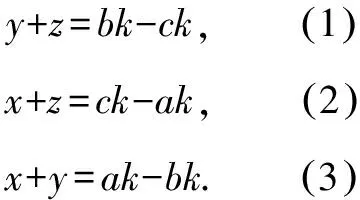
由1+2+3得2x+y+z=0,所以x+y+z=0.
二、变更条件或结论探求新结论,培养学生思维创造性
复杂的图形往往是简单图形的多次演变,复杂的问题往往是简单问题的综合,教师的教学可由简单的问题引入,多次进行“变式”,启发学生去积极探索,发现新结论,这对培养学生思维的创造性大有裨益.在平几教学中,我经常联想原命题的条件或结论的变化,引出一些新命题.

例2 如图1,AD是△ABC的高,AE是△ABC的外接圆直径,求证:AB·AC=AE·AD.
在讲解完这一例题的证明后,接着引导学生对命题的条件进行类比,指出例中的AD是△ABC的高,它是否可以是其他线段呢?若AD是∠A的平分线,AD是△ABC的边BC上的中线的情况下,结论又如何变化呢?若AE,AD分别与AB,AC的夹角相等,那么结论又怎样?经过学生的探索引出下面四个新命题:
(1)在△ABC中,∠A的平分线与边BC交于D,与它的外接圆交于E,则AB·AC=AE·AD;
(2)在△ABC中,BC边的中线AM延长后与它的外接圆交于点P,则AB·BP=AC·CP;
(3)在△ABC中,∠A的平分线与边BC交于D,与它的外接圆交于E,则AD2=AB·AC-BD·CD;
(4)在△ABC中,若∠BAE=∠CAD,则AB·AC=AE·AD.
原命题实际上是一个三角形的两边乘积定理:三角形一边上的高与外接圆直径的积等于其它两边的积.教学时指出此结论可直接应用,有关三角形的高、外接圆直径、内外角平分线与两边发生关系的某些问题,可用上述结论加以处理.
三、通过图形变换引导,培养学生思维的多向性
图形变换——即转换问题的形式内容,这是“变式”教学的一种形式.在教学中,若能利用图形的连续演变往往可以把一题推广而得到许多不同的题的特点,联系命题证法的多样性,培养学生思维的多向性.
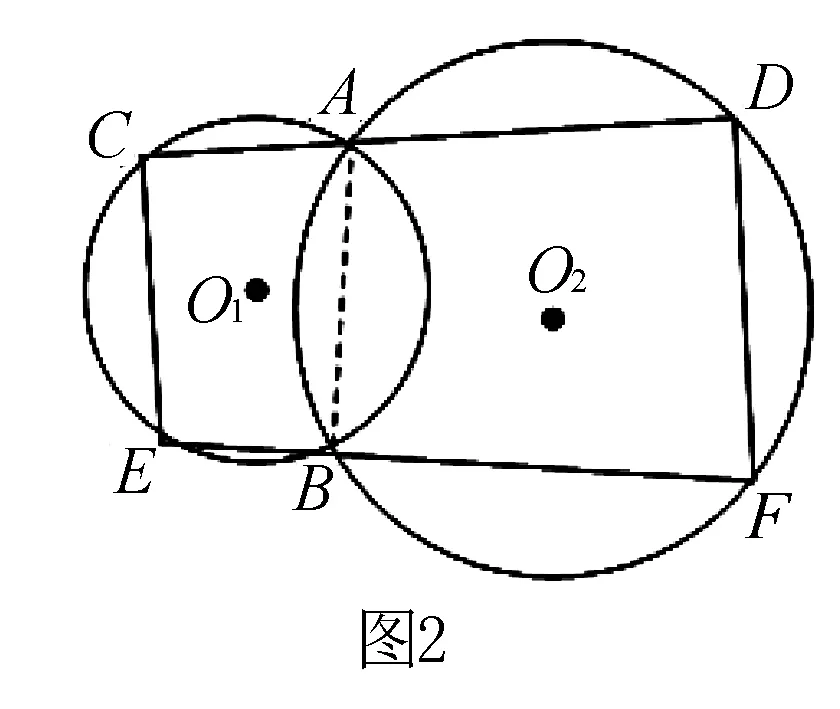
例3 如图2,圆O1和圆O2相交于A,B两点,经过点A的直线CD与圆O1交于点C,与圆O2交于点D,经过点B的直线EF与圆O1交于点E,与圆O2交于点F,求证:CE∥DF.
引导学生利用多种证法证明本例后,提出两个问题:
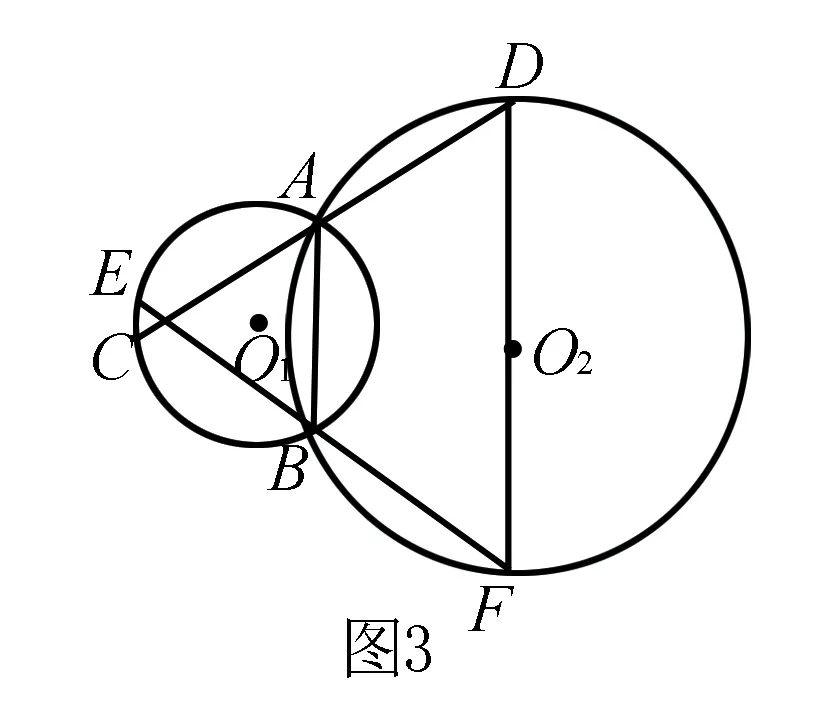
(1)若原命题条件不变,但不画图,那么按题意画图可能出现其他情况吗?学生自己动手画图,经过演变画出四种情况的图形.
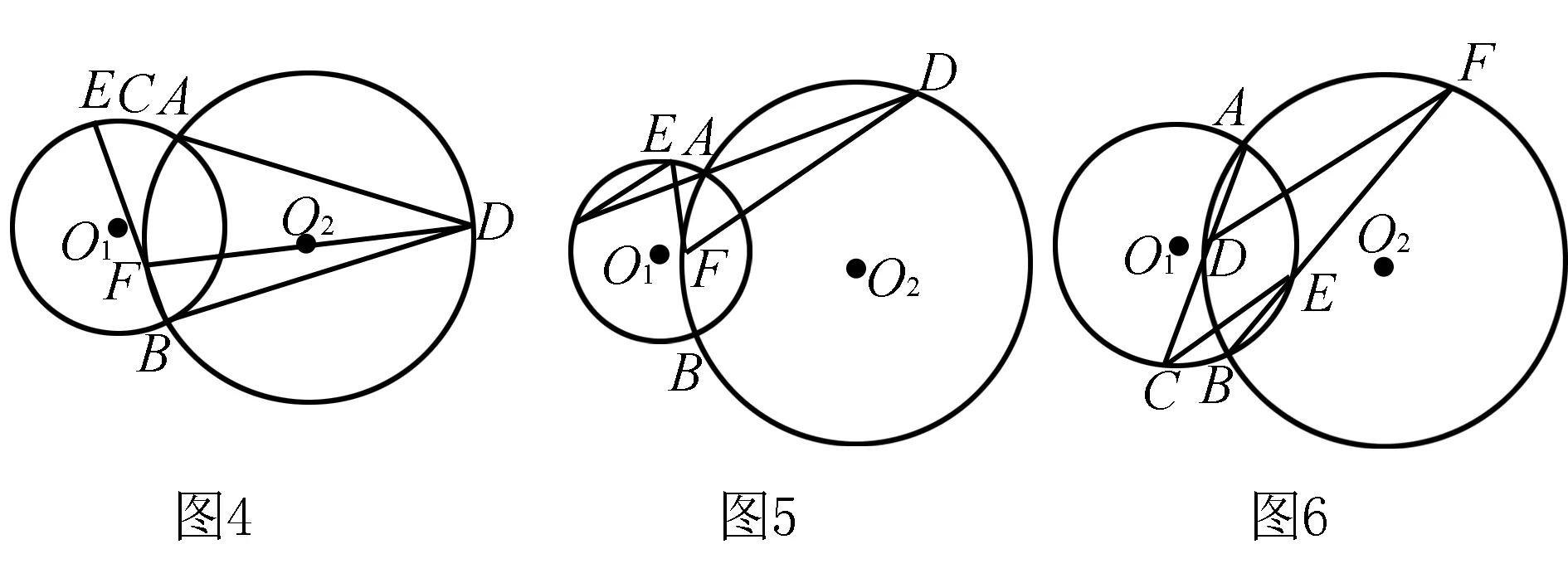
(2)结论CE∥DF是否保持不变?为什么?
估计学生答保持不变,这时因势利导,启发学生进行变形证明,这样,启迪学生思维,使学生又受到一次一题多解的训练.
四、通过条件和结论对等交换引导,培养学生思维的逆向性
心里学研究指出人的思维具有方向性,初中学生在学习数学过程中,也不可避免地会机械地套用某种固定的思维方法的顺向.例如,只习惯于“正向”的思维,不习惯于“逆向”的思维,只习惯于规定的步骤进行运算,不习惯于打破原有顺序寻求简便方法等, 这种定势思维的倾向如果得到强化,学生的思维将表现出惰性,是不利于教学的.因此,在教学中,必须加强“逆向”思维训练的培养,即加强对定义、定理、公式、法则的逆运用.通过条件和结论的对等交换,引导学生去论证、解题也是一条有效的方法.

这样“变式”,把习惯认为的条件和结论交换打破学生固有的思维定势,让学生在自己的知识结构中去寻觅求解的线索,勾画解题的思路,可逆性的思维也得到培养.
但值得注意的是有些命题将条件和结论交换后是否成立呢?须加以证明才能作出判断.平时发现有些学生对逆命题不加分析就作出判断,这种盲目的思维方法是不可取的,这里不防举一例.

把相同的个数的条件和结论完全交换后,所得如下四个命题:

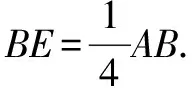


逆命题1、2、3可证明是成立的,但逆命题4是不成立的.

图7
分析连接EF,FD可证得△EBF∽△FCD,
∴∠1=∠2.
又∠2+∠3=90°,
∴∠1+∠3=90°,
∴∠EFD=90°.
∵FG2=EG·GD,这时G点也可能是ED的中点.
∴FG不一定垂直于ED,可见FG2=EG·GD成立时,G点不唯一.
∴逆命题4不成立.
显然,把结论和条件全部交换所得到的逆命题是不一定成立的,这类问题在课本中也经常出现,教学时要多注意,要全面地引导学生分析问题,可培养学生思维的深刻性.
在“变式”教学中,为了强化训练,我根据大纲、紧扣教材、循序渐进、区别阶段、针对实际、因人而异的原则,有目的地进行“变式”,如选编例题变式时,先由教师把几个形式不同,实际相同的题目,按先易后难顺序编成一组,然后引导学生分析、讨论得出结论,在课堂练习要训练变式,教师先出一题目,然后启发学生把它变形并加以训练,在安排习题时,要体现变式,即把难的变易,易的引难,使学生加深理解,也提高学习兴趣和解题速度.
实践使我深深体会到变式教学是结构教学中不可缺少的环节,是一条克服“题海战术”的有效途径,通过“变式”教学,使学生从中获得概念的认识,并提高识别、应变概括的能力,又减轻学生的负担,在教学中让学生自由去想象,去琢磨,这对发展学生思维的创造性创设了条件,在教学方法上一改过去“示范——模仿——练习”的模式.如果我们进一步明确“变式”的目的,遵循“变式”的原则,掌握“变式”的方法(即仿造、变更题型或叙述方式、引申结论等方法),教师具有娴熟的技巧,那么采用“变式”教学一定会达到“提高训练效率”的目的,教学质量无疑是会提高的.
参考文献:
[1]袁霞.浅析变式教学在初中数学教学中的应用[J]. 中学生数理化,2014(9).
[2]陈美珍.例谈初中数学变式教学[J]. 语数外学习,2015(8).
[3]顾浩.变式教学在初中数学教学中的应用[J]. 考试周刊,2015(96).
[4]张伟群.初中数学课堂教学中“变式教学”略谈[J]. 知识文库,2017(33).
[5]王兰花.论初中数学教学中的变式训练[J]. 学周刊,2017(33).

