找准关联 化繁为简
——由一道高考解析几何题引发的思考
沈文哲
(浙江省温州中学高三(1)班 325000)
解析几何以其计算繁琐著称,笔者在探索2017年高考数学浙江卷第21题得到启示,在解答解析几何求值时应尽量减少相关量之间的复杂联系,甚至切断不必要的联系,使表达式趋于简洁,达到简便计算的目的.
一、试题回放
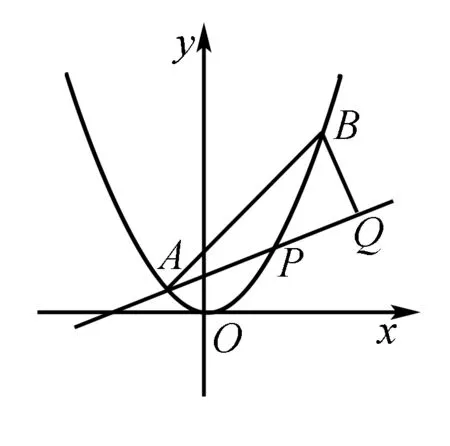

二、解法对比
1.我的解法
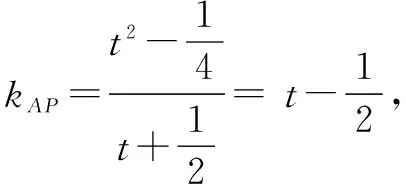
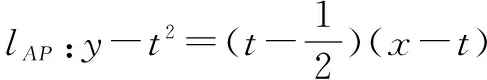
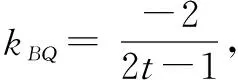

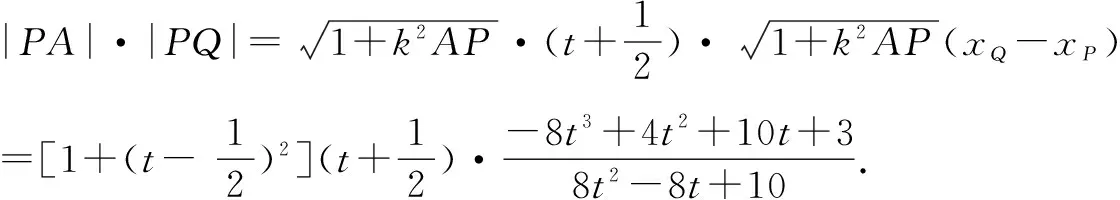
当从点P坐标入手时,|PA|·|PQ|表达式变得异常复杂,很难求得答案.
2.标准答案

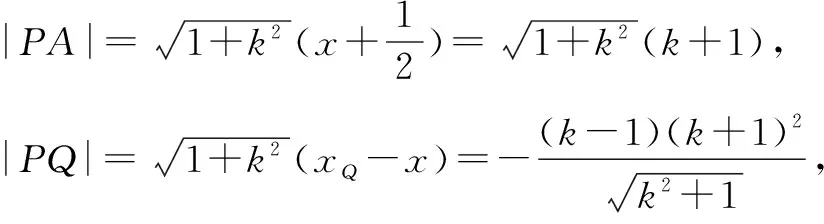
所以 |PA|·|PQ|=-(k-1)(k+1)3.
令f(k)=-(k-1)(k+1)3,
因为f′(k)=-(4k-2)(k+1)2,
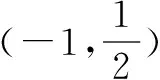
三、问题思考
笔者的解法与标准答案的切入点不同,即笔者是以点P定所有直线,而标准答案则是以直线定点的,为什么会产生如此大的差别?笔者经思考后,认为原因如下:
1.kAP、kBQ这一简单结论被笔者作为辅助条件,而标准答案则直接以此设直线.
2.以点定直线时使得kAP、kBP、点Q产生极为复杂的联系,而点Q与kAP为|PA|·|PQ|的关键,使点Q与kAP复杂化,必然不利于计算.
总的来说,对于解析几何计算求值,与表达式有关的量都应趋于简便,使其联系更加简单,甚至“切断”联系,这样才有利于解答.
四、问题应用

分析基本思路是利用y=k(x+c)与椭圆联立,利用韦达定理求解,但仔细思考后,使用y=k(x+c)会使AF1、BF1的长与F1产生联系,使得计算复杂化,因此必须切断AF1、BF1与F1的联系.
原始解法:设AB:y=k(x+c) 与椭圆联立,可得

最优解法:设AB:x=ty-c与椭圆联立,可得
(3t2+4)y2-6tcy-9c2=0.

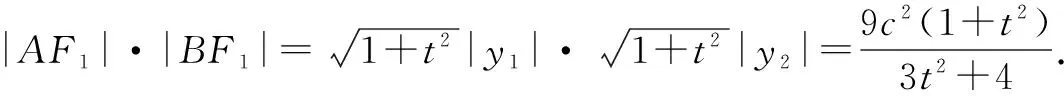

解析几何题求值时,量的关系是多样化的,我们应找准关联,选择最有利于解题的关系,做到化繁为简,使问题迎刃而解.
参考文献:
[1]蔡小雄.更高更妙的高中数学思想与方法[M].杭州:浙江大学出版社,2015(11).
[2]朱红喜.2012年高考数学江苏卷解析几何题别解[J].中学数学,2012(17).

