介绍立体几何中的一个有用结论

甘志国

(北京市丰台二中 100071)

在立体几何中有下面的一个有用结论：

图1

结论若两个相交平面内各有一条直线(均不是这两个平面的交线)互相平行，则这两条平行直线均与这两个平面的交线平行.

证明如图1所示，a⊂α,b⊂β,α∩β=l，a与l不重合，b与l也不重合，a∥b，下证a∥l.

由a⊄β，b⊂β,a∥b，得a∥β.

再由a⊂α,α∩β=l，得a∥l.

题1 证明：若一条直线与两个相交平面都平行，则这条直线与这两个相交平面的交线平行.

证明如图2所示，α∩β=l,c∥α,c∥β，下证c∥l.

图2

过直线c作平面γ,δ分别与平面α,β交于a,b.由c∥α可得c∥a，同理c∥b，所以a∥b∥c.再由上面的结论，得a∥b∥l，所以c∥l.

题2 证明：若一个平面和两个相交平面都垂直，则这个平面和这两个相交平面的交线垂直.

证明如图3所示，α⊥γ,β⊥γ,α∩β=l，下证l⊥γ.

因为α⊥γ,β⊥γ，所以可分别在α,β内作直线a⊥γ,b⊥γ，所以a∥b.再由上面的结论，得a∥b∥l，所以l⊥γ.

图4

解如图4，由AB∥CD及上面的结论，得平面VAB与平面VCD的交线l∥AB∥CD.设AB,CD的中点分别为E,F，可得∠EVF就是二面角B-l-C的平面角.可得正△VEF，所以∠EVF=60°，即所求答案为60°.

题4 如图5所示，直四棱柱ABCD-A1B1C1D1的底面是菱形，∠DAB=60°,AD=AA1,F,M分别是AA1,BD1的中点.

(1)求证：FM⊥面BDD1B1；

(2)求面BFD1与面ABCD所成锐二面角的大小.

图5 图6

解(1)如图6所示，设AC∩BD=O，连结OM，可得FM∥AO,AO⊥面BDD1B1，所以FM⊥面BDD1B1.

(2)由FM∥AO及上面的结论，得面BFD1与面ABCD的交线l∥FM∥AO，进而可得∠D1BD=45°为所求二面角的大小.

题6 (2016年高考全国卷Ⅰ文科、理科第11题)平面α过正方体ABCD-A1B1C1D1的顶点A，α∥平面CB1D1，α∩平面ABCD=m，α∩平面ABB1A1=n，则m,n所成角的正弦值为( )

解A.如图7所示，因为平面α∥平面CB1D1，所以平面α与平面ABCD的交线m平行于平面CB1D1与平面ABCD的交线l.

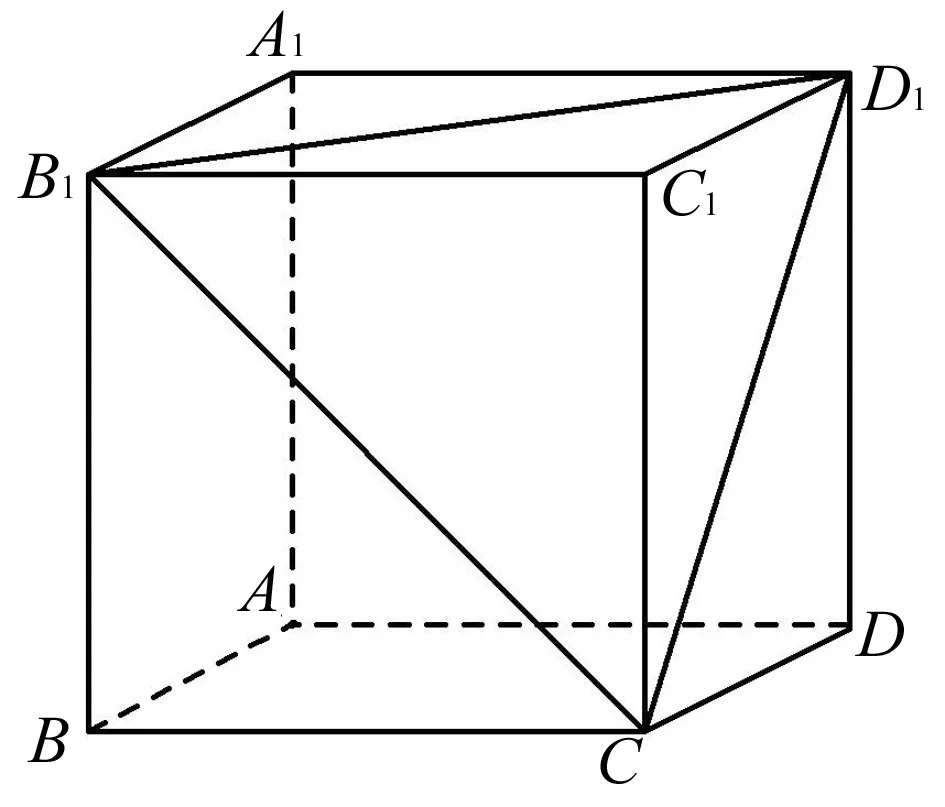
图7

因为在正方体中平面ABCD平行于平面A1B1C1D1，BD∥B1D1，所以由上面的结论可得l∥B1D1，再得m∥B1D1.

同理，n平行于平面CB1D1与平面ABB1A1的交线．

因为平面ABB1A1∥平面CDD1C1，所以平面CB1D1与平面ABB1A1的交线平行于平面CB1D1与平面CDD1C1的交线CD1，所以n∥CD1.

所以m，n所成的角即为B1D1，CD1所成的角.

图8

题7 (2013年高考湖北卷理科第19(1)题)如图8，AB是圆的直径，点C是圆O上异于A，B的点，直线PC⊥平面ABC，E，F分别是PA，PC的中点.记平面BEF与平面ABC的交线为l，试判断直线l与平面PAC的位置关系，并加以证明.

解如图8所示，由EF∥AC及上面的结论，得l∥AC，所以直线l∥平面PAC.

图9

题8 (2013年高考安徽卷理科第19(Ⅰ)题)如图9，圆锥顶点为P.底面圆心为O，其母线与底面所成的角为22.5°.AB和CD是底面圆O上的两条平行的弦，轴OP与平面PCD所成的角为60°.证明：平面PAB与平面PCD的交线平行于底面.

解由AB∥CD及上面的结论，得平面PAB与平面PCD的交线平行于AB，进而可得欲证.

参考文献：

[1]人民教育出版社，课程教材研究所，中学数学课程教材研究开发中心. 普通高中课程标准试验教科书( 必修)数学4(A版)[M]. 北京:人民教育出版社,2014.