平面几何性质在圆锥曲线中最值的应用

袁明焕

(福建省寿宁县第一中学 355500)

一、利用几何性质简化最值问题利用几何性质减少做题失误

圆锥曲线最值问题一直是高中数学的重点和难点之一.圆锥曲线是几何图形的一种，最值问题，研究的量也是几何量.所以在解决圆锥曲线的最值问题过程中，经常会用到圆锥曲线的定义方程以及几何性质.通过利用几何性质来解答圆锥曲线的最值问题，能够从一定程度上简化问题，节约做题时间，提高做题效率.椭圆是平面内两定点F1,F2的距离和等于常数2a的动点P的轨迹.而双曲线则是平面内一动点P与两个定点F1，F2的距离的差的绝对值等于常数的点的轨迹. 即│PF1│-│PF2│±2a.

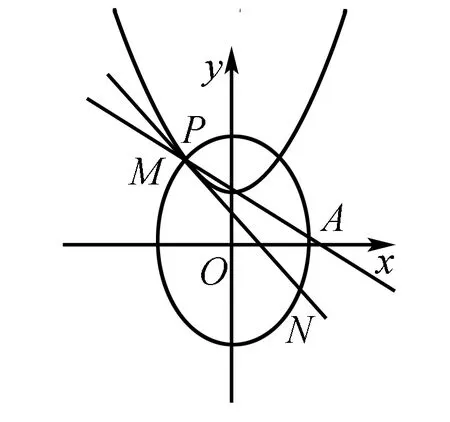
首先咱们来分析一下这一道题，这是一道比较经典的题型，第一问求椭圆的方程非常简单，但是第二问难度就比较大了，把椭圆和抛物线结合起来，光看图形就能感觉到题目很难，对学生来说比较复杂和繁琐.但是利用几何性质等知识我们就可以很容易的把题目分析清楚，并解出答案.这道题考查的是学生对于几何基本思想的掌握和一种综合的解题技能.只要我们好好分析就不难发现这道题主要用到的知识点是椭圆、抛物线的几何性质，还有直线和椭圆抛物线的位置关系等基础知识.

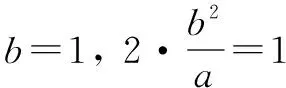
(2)如图，我们可以先把M,N,P点的坐标设出来，设M点的坐标为(x1,y1),N点的坐标为(x2,y2),P点利用点斜式来表示就是(t,t2+h),根据这个条件我们可以知道，抛物线C2在点P处的切线斜率为k=2t，直线MN的方程为y=2tx-t2+h然后如果我们再把这个式子代入到椭圆C1的方程中去，就会得到一个方程组，

4x2+(2tx-t2+h)2-4=0

整理得，

①4(1+t2)x2-4t(t2-h)x+(t2-h)2-4=0.

然后图中给出的另一个条件是直线MN与椭圆C1有两个不同的交点.我们需要用这个条件来判断Δ的正负，所以①式中Δ1=16[-t4+2(h+2)t2-h2+4]>0.

又因为从题目所给出的条件中我们可以看出来x4=x3,

∴t2+(1+h)t+1=0③,

∴Δ2=(1+h)2-4≥0.

解得h≥1或h≤-3

接下来我们来分情况进行分析，当h≤-3时，h+2<0，4-h2<0，在这种情况下不等式②不能成立，∴h≤-3不能成立，所以h≥1.很多人做到这一步就以为完成了，但是其实我们还需要把h=1代进去检验一下，看看结果是否正确，从而避免失误.当h=1时，把它代入方程③式得t=-1，然后我们再把t=-1,h=1代入不等式②中去，可以成立，所以h的最小值是1.

通过完整的解题过程来看，这道题在解答过程中充分地利用了圆锥曲线的几何性质，具有很强的技巧性，通过对于几何性质的分析，思路清晰，过程比较简单，对于简化题目非常有帮助，再加上验证过程，非常有利于降低做题失误.

二、利用几何性质简化最值问题

几何法是圆锥曲线最值问题的基本解决方法之一，它的原理是通过分析几何量之间的相互关系，利用平面几何的知识得到解决方法.例如，我们可以利用抛物线上的点到某个定点和焦点的距离之和来构建方程解决最值问题.几何的性质非常简洁明了，相对于代数法而言，它有利与我们在做题中减少失误，提高正确率.有些时候我们也可以将圆锥曲线的相关问题先转化为平面几何的相关问题，再利用平面几何的知识，像对称性、三角形的三边相互关系、平行线间距离等进行解答.

例如：已知点M(3，2)，F为抛物线y2=2x的焦点，点P在该抛物线上移动，当|PM|+|PF|取最小值时，点P的坐标为____．

分析本题若建立目标函数来求|PM|+|PF|的最小值是困难的，若巧妙地利用抛物线定义，结合图形则问题不难解决．

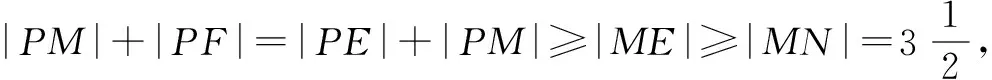
利用这种转化为几何性质的方法来解答最值问题，能够简化解题步骤，提高解题效率，我们应该多加练习和运用.

圆锥曲线问题中经常会遇到一些求极值的问题，今天给大家介绍的这两种运用平面几何性质解决圆锥曲线最值问题的方法，经过了深入的分析和大量的应用实践，事实证明这是一种独特但又并不离经叛道的好方法，希望大家可以认真思考，举一反三，有所收获和飞跃.

参考文献：

[1]程森旺. 圆锥曲线定义在解题中的应用[J].教育界,2010(25).

[2]赵雪英. 平面几何性质在圆锥曲线中的应用探究[J].教育界,2016(16) .

[3]顾洁. 圆锥曲线性质在求解圆锥曲线的最值问题中的应用[J].教育教学研究,2015(51).