围栅硅纳米线MOSFET器件的仿真研究

刘一婷，宫 兴，闫 娜

（沈阳工业大学信息科学与工程学院，沈阳110870）

1 引言

随着半导体器件尺寸的缩小，无掺杂短沟道的围栅金属-氧化物-半导体场效应晶体管（Gate-allaround MOSFET,简称GAA-MOSFET）凭借其优良的栅控特性发展为下一代半导体电子器件的重要候选之一[1]。当前MOSFET的尺寸已经下降到20nm以下领域，因此量子输运在MOSFET器件中成为非常重要的机制，用量子输运相关的参数可以更精确地描述弹道效应、量子效应、隧穿效应等器件特性[2-5]。用NEGF、S-P等数值计算方法来对复杂结构下器件模型的载流子特性进行仿真，现在已经能够实现；对于N型GAA-MOSFET的特性，也已经通过大量的仿真得以验证[6]。然而由于纳米尺度下P型半导体的能带结构复杂，而空穴的有效质量、输运特性、状态分布在很大程度上依赖于此，所以对于P型GAA-MOSFET的研究仿真此前还没有实现过。本文将利用Silvaco TCAD Atlas仿真系统的数值计算功能对P型GAA-MOSFET的特性进行仿真研究，探讨不同条件下P型GAA-MOSFET的特性。

2 模型与基本理论

2.1 GAA-MOSFET结构模型

GAA-MOSFET的整体结构如图1中的立体示意图(a)所示：外圈部分是栅极，它将沟道部分完全包裹住；柱型沟道的两端是GAA-MOSFET的源、漏两极。图1中的(b)、(c)则为沿着器件截面B、C方向的剖面图。图1(a)中的Z轴是空穴的传输方向；(b)中的R是沟道的半径，是氧化层的有效厚度；(c)中的分别是半径分量和角分量。

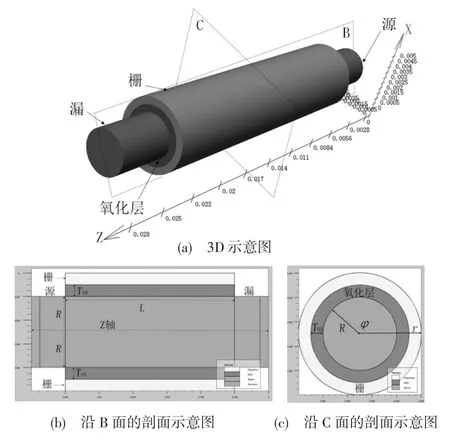
图1 GAA-MOSFET结构示意图

本文的所有数值仿真都是在Silvaco TCAD的Atlas环境下进行的，具体用到FIXED.FERMI、NEGF_MS、NPRED.NEGF、EIGEN、SP.SMOOTH等模型；仿真预设定的具体参数如表1所示。

表1 GAA-PMOSFET仿真预设参数

2.2 基本理论

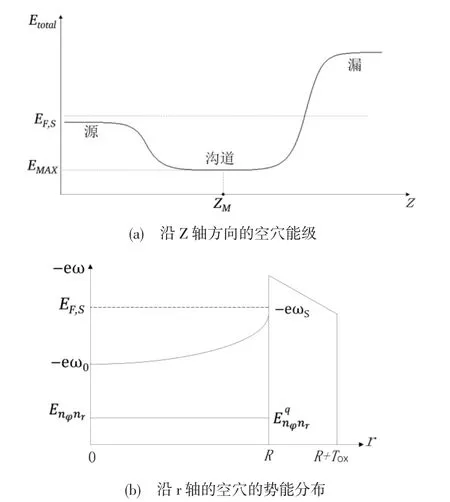
图2 空穴能级及势能分布图

沟道中的空穴的能级可以由以下公式给出：

具体计算按参考文献[7]和[8]进行。

由于氧化层价带能级高，沟道内的可移动空穴被束缚在量子阱中。根据量子力学可知，沟道处的空穴能级分布是离散的，在处空穴的束缚能级可以由薛定谔方程得出：

当沟道长度小于载流子的平均自由程时，沟道内的空穴以弹道或准弹道输运方式在沟道内传导。假设源漏是理想的储层，向沟道里注入足够的空穴，空穴的弹道电流就可以通过Landauer公式计算得出如下：

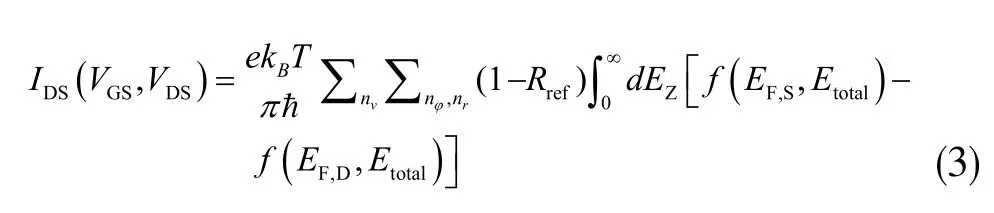
3 结果与讨论

基于上述分析，使用Silvaco ATLAS对P型GAA-MOSFET器件结构与性能进行仿真研究。图3给出了在处栅极电压与空穴能级的关系，图3(a)是不同空穴子带数情况下栅极电压与空穴能级的关系，方形点是仅有一条子带时能级随栅压的变化情况，圆点和三角点分别是考虑两条子带时重空穴和轻空穴的能级与栅极电压的关系曲线；图3(b)是不同半径R下处栅极电压与空穴能级的关系曲线。图中是轻空穴能级是重空穴能级是源极空穴的费米能级。

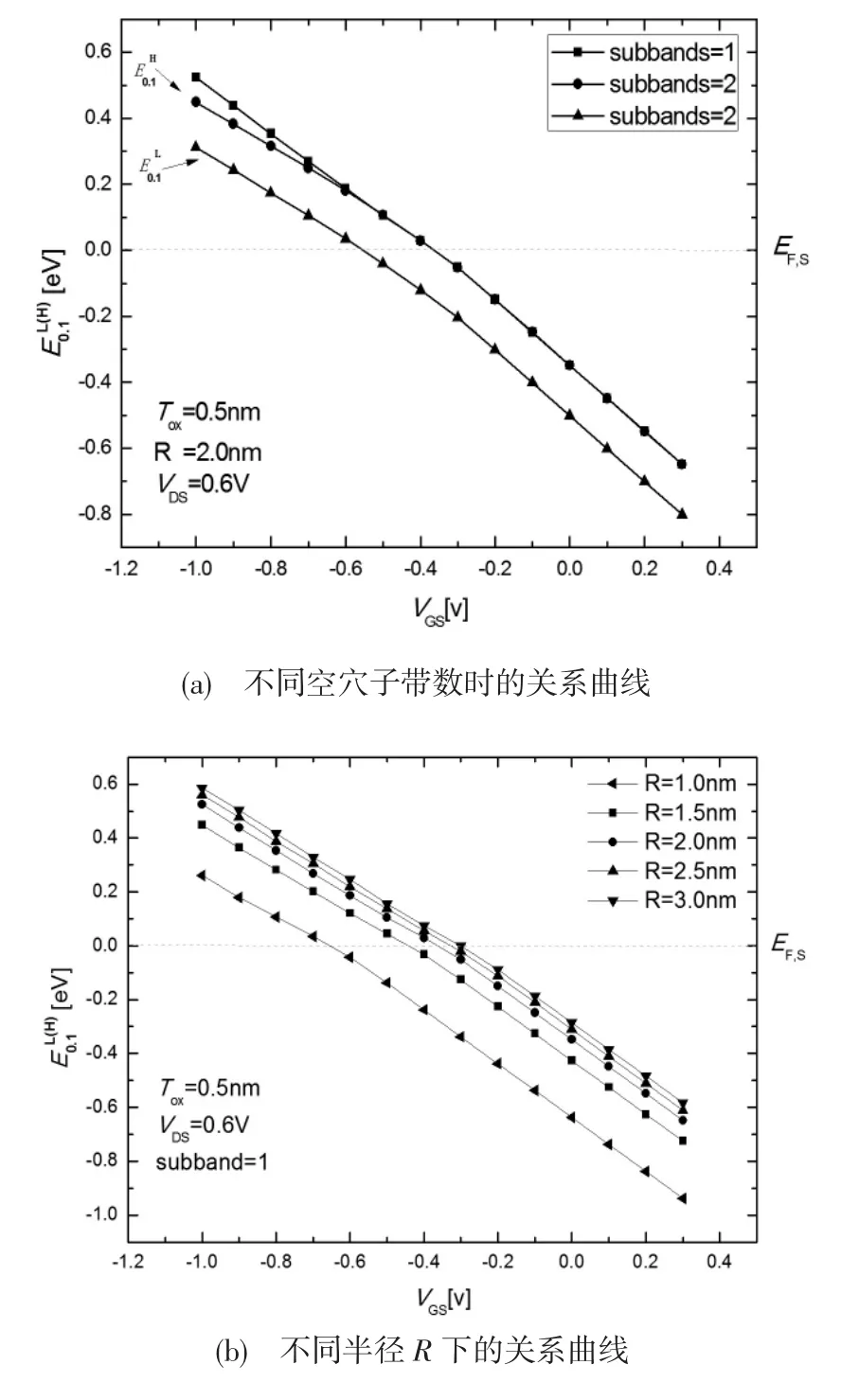
图3 处能级分布图

当沟道内的载流子被激发到能级上时会导致沟道内电荷数量上升，电荷数量的上升又会使沟道内的静电分布发生变化，从而导致空穴的能级上升，当其高于费米能级时，空穴开始被激励到能级上。从图3(a)可以看出当考虑两条子带时，载流子不仅会被激发到最低子带，还可能被激发到第二子带上。图3(b)展示了半径对能级的影响，在同等条件下半径R越大，能级越靠近价带边缘，空穴也就越容易被激励到空穴能级上。

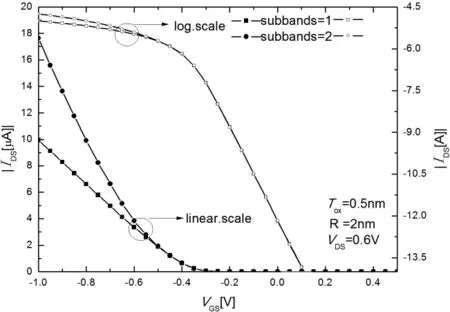
图4 考虑不同子带时GAA-MOSFET的转移特性

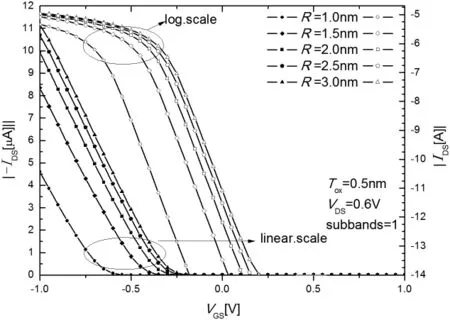
图5 不同半径时GAA-MOSFET的转移特性

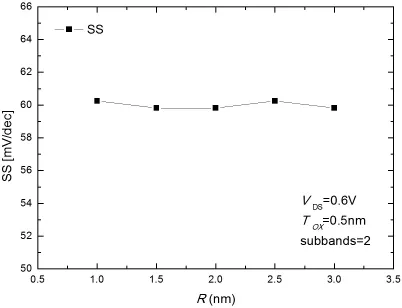
图6 不同R值的亚阈值摆幅

由图6可知，GAA-MOSFET的亚阈值摆幅（SS）大约都在60mV/dec左右。这接近室温条件下（T=300K）MOS型器件SS的理论最小值，即59.6mV/dec。同时通过图5、图6可以看出半径R的变化对GAA-MOSFET的漏电流有影响，但对亚阈值摆幅的影响很小，基本可以忽略。

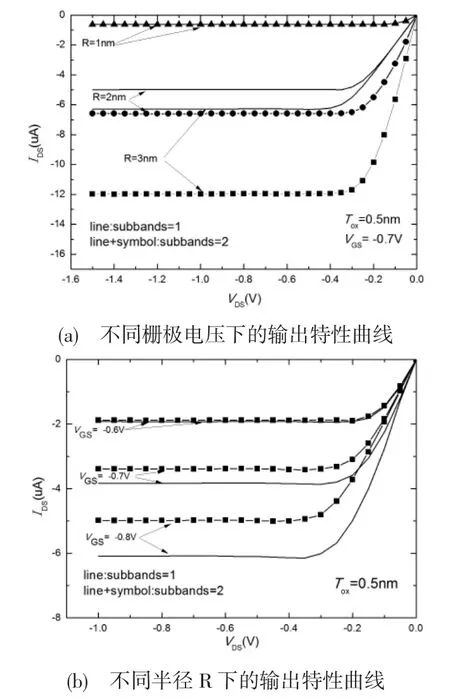
图7 GAA-MOSFET的输出特性

从图7(a)可以看出GAA-MOSFET的输出特性曲线与传统结型场效应管一样，也分为线性区、非线性区和饱和区。在相同栅极电压下，两条子带比仅考虑一条子带时的漏电流大。图7(b)中Line是考虑一条子带时的输出特性曲线，Line+symbol是考虑两条子带时的输出特性曲线，可见漏电流随着半径的减小而减小。当半径为1nm时考虑两条子带和考虑一条子带时的漏电流曲线基本相同，这主要是因为半径为1nm时载流子很难被激励到第二子带处。

4 结束语

对P型GAA-MOSFET器件的特性进行了深入的仿真研究，除了讨论半径大小对GAA-MOSFET特性的影响，还考虑了不同子带数对GAA-MOSFET的影响，结果表明对于GAA-MOSFET器件，因其量子限制效应的存在，我们不得不考虑到它的能级分裂问题；分别考虑了一个子带和考虑两个子带的情况，发现两个子带时GAA-MOSFET的性能更优良。但对现实情况中的空穴来说能级不止两个，所以对于GAA-MOSFET能级分裂问题，还有待后续的进一步研究。

[1]MOORE G E.Progress in digital integrated electronics[C]//Electron Devices Meeting,1975 International.IEEE Xplore,2006:11-13.

[2]艾罗拉.用于VLSI模拟的小尺寸MOS器件模型[M].张兴，李映雪，译.北京：科学出版社,1999.AIROLA N.Small size MOS device model for VLSI simulation[M].ZHANG Xing,LI Yingxue,transl.Beijing:Science Press,1999.

[3]ZHANG L,WANG S,MA C,et al.Gate underlap design for short channel effects control in cylindrical gate-allaround MOSFETs based on an analytical model[J].Iete Technical Review,2012,29(1):29-35.

[4]SARKAR A,DE S,DEY A,et al.Analog and RF performance investigation of cylindrical surrounding-gate MOSFET with an analytical pseudo-2D model[J].Journal of Computational Electronics,2012,11(2):182-195.

[5]柯导明陈军宁.数学物理方法[M].北京：机械工业出版社,2008:206-211.KE Daoming CHEN Junning.Mathematical and physical methods[M].Beijing:China Machine Press,2008:206-211.

[6]COLINGE J P.Multiple-gate SOI MOSFETs[J].Solid State Electronics,2004,48(6):897-905.

[7]CHENG H,UNO S,NUMATA T,et al.Analytic compact model of ballistic and quas-ballistic cylindrical gate-allaround metal-oxide-semiconductor field effect transistors including two subbands[J].Japanese Journal of Applied Physics,2013,52(4S):71-132.

[8]HE C,UNO S,NAKAZATO K.Analytic compact model of ballistic and quasi-ballistic transport for cylindrical gate-all-around MOSFET including drain-induced barrier lowering effect[M].Springer-Verlag New York,Inc.2015.