一种改进的SAD目标跟踪算法
赵柏山,刘佳琪,王禹衡
(沈阳工业大学信息科学与工程学院,沈阳110870)
1 引言
目标跟踪作为机器视觉研究领域的热门话题之一,在军事、医学、工业等领域得到广泛应用,具有广阔的应用前景。基于模板匹配的目标跟踪算法,由于其计算量低,局部抗干扰能力强,在信噪比较低的情况下依然可以有效跟踪目标,更是被广为采用[1]。
模板匹配主要针对目标的外观进行跟踪。由于受外界因素的影响,目标往往会由于受到遮挡等干扰而跟踪失败。传统的模板匹配算法是单纯依据模板的灰度值,用待搜图像与模板等大图像进行灰度匹配,但是当遮挡、干扰、形变等情况发生时,图像的灰度值会随之变化,致使目标跟踪失败。针对这一情况,国内外学者通过研究提出了一些解决方法,例如:基于小波变换的图像预测[2]、利用meanshift算法的迭代[3]、基于粒子滤波进行多目标跟踪[4]、SSD与MCD融合算法[5]、基于核相关滤波器的TLD算法[6]、利用前后向光流法对目标跟踪失败进行补救[7]等。
针对模板匹配跟踪算法抗遮挡能力差的缺点,对SAD算法进行了改进。以SAD矩阵为基础,通过对目标区域和与目标区域有交集的背景区域设定不同权重的系数,增加目标区域权重,减小背景区域的影响,判断目标跟踪有效性,在判定目标跟踪失败时进行模板更新,来保证目标持续有效跟踪,提高了目标跟踪的有效性与准确性。
2 目标跟踪算法
2.1 SAD算法
绝对误差和SAD(Sum of Absolute Difference)算法是基于灰度的模板匹配算法[8]。其原理是,通过模板图像与待搜索图像进行相似性度量来作判断,获得目标图像的准确位置,从而实现目标的跟踪效果。如图1所示,T是模板图像,尺寸为m×n;S是待搜索图像,尺寸是M×N;将模板图像在待搜索图像上进行遍历。逐次令模板图像与待搜图中的大小与模板图像相同的图像进行相似性度量计算,相似度最相近的位置,即目标图像的位置。SAD算法的计算公式为

其中i,j为子图的左上角坐标。由图1可知在模板图像遍历的过程中,SAD形成一个矩阵,大小为M-m+1,N-n+1。其中,每一个数值分别代表模板图像与待搜索图像对应子图的绝对误差和。

图1 SAD算法原理图
由公式1可知,SAD矩阵中的每个值对应的是模板图像与搜索子图对应位置的像素差的绝对值求和,所以SAD矩阵中数值越小,表明两个图像越相似。当数值为0时,代表两个矩阵完全重合。
正常情况下,SAD矩阵内的最小值即为目标图像的位置。但是当干扰出现时,目标图像可能会受到遮挡等影响,造成最后的SAD矩阵内最小值位置并不是实际目标的位置,从而发生目标跟踪失败。由图2可知,模板在待搜索图的遍历过程中,SAD矩阵最小值对应目标位置,但是在SAD矩阵周围的图像也会与目标图像存在一定程度的交集,交集越多,SAD值越小。SAD矩阵最小值周围数值的灰度与目标图像存在一定的相似性,当外界干扰出现时,这种相似性会不断减弱,基于这一点,对SAD算法进行改进,以SAD矩阵最小值为中心,通过矩阵分块设计,选取不同大小矩阵并设置不同权重系数,能提高目标跟踪的准确性和有效性。

图2 模板遍历过程
矩阵大小的选取如图3所示。正常情况下模板在待搜索图中遍历的过程会有一部分与目标图像存在交集,这些交集在SAD矩阵中反映出来的就是目标坐标(i,j)周围的数值。模板图像大小为m×n,目标的中心往往也是处于模板图像的中心位置。由此,以目标位置(i,j)为中心,构建不同大小矩阵,可使背景图像所占比例减少。

图3 矩阵分块区域选择
以(i,j)为中心,其中实线矩形边框表示矩阵I1,长和宽分别选取m和n,四个坐标点分别为(i-m/2,j-n/2)、(i-m/2,j+n/2)、(i+m/2,j-n/2)、(i+m/2,j+n/2),虚线矩形表示矩阵I2,同样为以(i,j)为中心,大小为2(m-1),2(n-1)并且剥除I1矩阵位置的像素。
I1和I2矩阵所占的权重设为w1和w2,取值为w1=1和w2=0.5,这样新构成矩阵包含了所有与目标图像有交集的搜索矩阵。降低遍历范围,提高搜索有效性。矩阵分块具体计算公式如下:

2.2 SSD算法与MCD模板更新
以SAD矩阵为模板,通过SSD算法对矩阵进行目标跟踪匹配。SSD(Sum of Squared Difference)即误差平方和算法,与SAD算法类似,它利用模板图像与待搜索图像进行遍历,通过计算对应位置像素进行做差求平方和。模板T由第一帧获得,S(i,j)为待搜索图像,与之后每帧图像获取的目标进行SSD匹配,公式如下:

为了判定目标跟踪效果,采用MCD(Maximum Close Distance)算法来作判断[9],MCD即最大邻近距离,又叫相关置信度,如下式:

MCD反映的是模板图像之间的相似数目的多少,MCD值越大,两个模板越相似,反之两个模板不匹配。设定阈值T_MCD(本设计T_MCD选取为40),通过比较第一帧模板图像与当前帧获取的目标图像,进行对应点的灰度绝对差值运算。当差值小于T_MCD时,那么认为两点相似。MCD值计数为1,否则MCD值为0。最后MCD会形成一个相关曲面,峰值点即为最相似点,也就是我们要找的目标位置。
由于目标遮挡、干扰、甚至目标本身发生微小的形变等情况的存在,采取MCD的值作为判断是否需要模版更新的依据,由于本设计以SAD矩阵为模版核心,取SAD内包含全部目标和部分背景区域的图像为跟踪基础,所以MCD模版为第一帧获取的SAD跟踪图像,大小为2(m-1)×2(n-1)。MCD最大值即为2(m-1)×2(n-1),代表完全匹配。判定模版更新条件如下式:

如果单纯依靠初始模版进行匹配跟踪,很容易造成目标的错跟和漏跟。所以就需要在跟踪失败时能及时、准确地更新目标模版。在文献[9]中采用的方法是,将前一帧模版和当前帧进行融合,通过匹配不同的权值,按照其权重的大小进行有效融合。此法虽在一定程度上提高了匹配的鲁棒性,但单纯的两帧仍然会受到外界因素的很大影响。鉴于此,本设计的模版更新采用多帧更新的方法。由于初始模版包含图像的基本信息,前一帧图像和当前帧图像反映了目标图像的变化,所以可将初始模版图像、前一帧图像、当前帧图像分别赋予一定权值,分别为ɑ0、ɑ1、ɑ2,如式(6)所示,最终权重系数和为 1,合成一个新的模版继续进行目标的匹配跟踪。
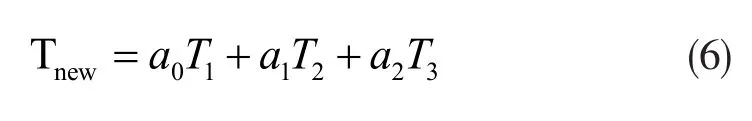
式(6)中,Tnew为合成后的新模版图像,T1、T2、T3分别为初始模版、前一帧模版和当前帧模版图像;权重的取值则为 ɑ0=0.4,ɑ1=0.3,ɑ2=0.3。
3 仿真实验结果
3.1 目标发生遮挡的情况
本次测试共150帧,图4是单独使用SAD算法进行匹配的跟踪效果,目标是路上行走的行人。在行人行进的过程中会被前面的人遮挡。

图4 目标被遮挡情况下的SAD算法跟踪效果
图4(a)是目标模版,在第一帧图像中目标无遮挡,目标能被准确找到、获取位置并用边框标记出来;图4(b)所示为第15帧图像,目标行人在行走过程中被前面行人部分遮挡,遮挡面积小于20%,目标仍被正确跟踪并标记边框;图4(c)所示为第41帧图像,目标被遮挡面积超过90%,目标跟踪失败,没有准确捕获到目标的正确坐标;图4(d)为第45帧图像,目标重新出现,正确捕获目标并标记目标位置。
图5为使用本算法对相同场景下的遮挡目标进行跟踪的效果。

图5 本算法在目标遮挡时的跟踪效果
图5(a)是目标模板图像;图5(b)是目标被少部分遮挡的情况,本算法可以准确追踪目标;图5(c)是目标被遮挡面积超过90%的情况,通常的SAD算法已无法找到目标,但本算法依然可以准确找到目标位置并进行准确标记;在图5(d)中,目标摆脱遮挡重新出现,目标被准确地找到并进行标记。可见,算法实现了在不利情况下对目标的准确有效的跟踪。目标跟踪判断统计结果如表1。

表1 目标被遮挡时的判定结果统计
3.2 目标发生形变的情况
本视频共100帧,如图6所示,图中的目标本身会发生形变。图6(a)所示为目标模板图像;图6(b)为第30帧图像,SAD算法跟踪的结果,由于目标人物的走动及脸部的变化,算法无法捕获正确目标;图6(c)为相同的图像,应用改进后的算法,能够正确找到目标位置并标记边框。发生形变情况下的目标跟踪判断统计结果如表2。

图6 SAD与本算法对发生形变的目标跟踪效果对比

表2 目标发生形变时的判定结果统计
4 结束语
通过改进的SAD模板匹配目标跟踪算法,并利用SSD算法,进行模板的相似性匹配。利用多帧MCD算法判断模板更新需求,实时准确地更新目标模板,保证目标跟踪的准确性。实验表明,在目标受到遮挡或者目标本身发生形变的情况下,改进后的算法仍能够准确搜索到目标位置并进行标记。相比于原SAD算法,改进算法在目标抗遮挡和抗形变的能力上得到了显著的提高,具有十分可观的实用价值和推广潜力。
[1]高文,朱明,贺柏根,等.目标跟踪技术综述[J].中国光学,2014,7(3):365-375.GAO Wen,ZHU Ming,HE Baigen,et al.Overview of object tracking technology[J].Chinese Optics,2014,7(3):365-375.
[2]GHASEMBAGLOU M,Toroghihaghighat A Haar wavelet based distributed predictive target tracking algorithm for wireless sensor networks[M]//Advances in Computational Science,Engineering and Information Technology.Springer International Publishing,2013:207-219.
[3]郭晓冉,崔少辉,曹欢,等.跟踪窗自适应的捷联导引系统目标跟踪算法[J].兵工学报,2014,35(10):1604-1611.GUO Xiaoran,CUI Shaohui,CAO Huan,et al.Object tracking algorithm for strapdown guidance system with adaptive tracking window[J].Acta Armamentarii,2014,35(10):1604-1611.
[4]李天成,范红旗,孙树栋.粒子滤波理论、方法及其在多目标跟踪中的应用[J].自动化学报,2015,41(12):1981-2002.LI Tiancheng,FAN Hongqi,SUN Shutong.Theory and method of particle filtering and its application in multiobject tracking[J].Acta Automatica Sinica,2015,41(12):1981-2002.
[5]胡铟,杨静宇.适用于遮挡情况的SSD和MCD融合跟踪算法[J].系统仿真学报,2010,22(4):908-911.HU Yin,YANG Jingyu.SSD and MCD fusion tracking algorithm for occlusion[J].Journal of System Simulation,2010,22(4):908-911.
[6]诸小熊,江加和.基于核相关滤波器的目标跟踪算法[J].应用科技,2017,44(3):48-53.ZHU Xiaoxiong,JIANG Jiahe.Object tracking algorithm based on kernel correlation filter[J].Applied Science and Technology,2017,44(3):48-53.
[7]KALAL Z,MIKOLAJCZYK K,MATAS J.Forwardbackward error:Automatic detection of tracking failures[C]//International Conference on Pattern Recognition.IEEE Computer Society,2010:2756-2759.
[8]冯俊惠,肖阳辉,王恩德,等.一种基于SAD的相关跟踪有效性判断方法[J].微电子学与计算机,2015,32(11):101-104.FENG Junhui,XIAO Yanghui,WANG Ende,et al.A correlation tracking validity judgment method based on SAD[J].Microelectronics&Computer,2015,32(11):101-104.
[9]赵清华.基于FPGA的目标跟踪算法的设计与实现[D].北京:中国科学院大学,2014.ZHAO Qinghua.Design and implementation of object tracking algorithm based on FPGA[D].BeiJing:University of Chinese Academy of Sciences,2014.

