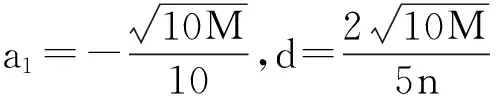数形齐管 多元推进*
——高考平面向量复习策略研究
● ●
(元济高级中学,浙江 海盐 314300) (海盐高级中学,浙江 海盐 314300)
平面向量是高中数学的重要内容,也是高考的热点之一,是浙江省数学高考命题的亮点之一.平面向量兼顾“数”与“形”的两重性,形成了其独特的知识体系与思想方法体系,但平面向量又与代数、几何、三角、不等式与数列有着紧密的联系.大部分学生对于平面向量知识掌握不好的原因在于不能灵活地在“数”与“形”之间进行转换或转换的方向不正确.而所有的数学学科能力与素养必然扎根于概念,由此内化为知识网络的节点,构建自己的结构化知识网络系统,进而深度挖掘问题的数学本质,基于本质优化策略——提出问题的本质解法、发展优化解法,整合知识、方法与思想实现提升数学核心素养[1].下面笔者结合平时的教学与高考试题解答后的思考,在深化学生对平面向量核心概念的理解与掌握、提高学生处理平面向量综合能力、形成数学核心素养等方面进行探究.
1 代数背景
1.1 线性运算基底化
平面向量的线性运算及其几何意义,尤其突出了对平面向量基本定理和向量三点共线定理的理解.所谓基底化,是指根据题设与目标选择适当的“基底”,并用“基底”表示有关向量,以实现化归的一种思维方式.基底是平面向量基本定理的“灵魂”,技术核心是“如何选择基底,简化运算”.
例1如图1,在ABCD中,点E是边BC(靠近点B)的三等分点,F是AB(靠近点A)的三等分点,P是AE与DF的交点,若则λ+μ=______.

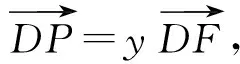

故
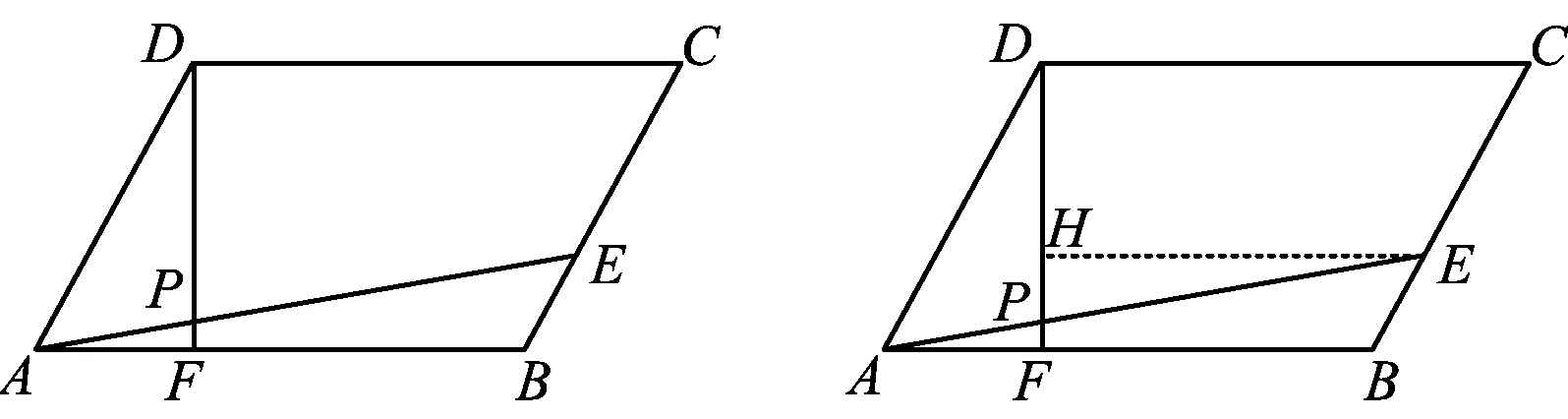
图1 图2
解法2如图2,过点E作EH∥AB交DF于点H,易知
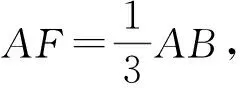
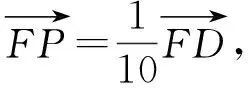
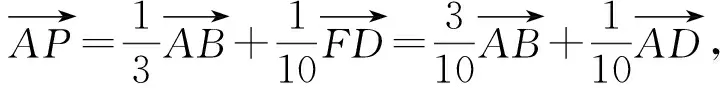
故


推广1基底前的系数λ1,λ2的范围与点P位置的关系:分别记过点A且与BC平行的直线为l1,直线BC,AB,AC为l2,l3,l4,则
1)当点P与点A在直线l2的异侧⟺λ1+λ2>1.
2)当点P在直线l2与l1之间⟺0<λ1+λ2<1.
3)当点P与l2在直线l1的异侧⟺λ1+λ2<0.
4)当点P与点C在直线l3的异侧⟺λ1∈R,λ2<0;当点P与点C在直线l3的同侧⟺λ1∈R,λ2>0.
5)当点P与点B在直线l4的异侧⟺λ1<0,λ2∈R;当点P与点B在直线l4的同侧⟺λ1>0,λ2∈R.
1.2 几何背景坐标化
坐标化是通过构建直角坐标系,将向量改用坐标来表示,使向量问题转化为代数问题来处理的一种思维方式,是解决向量问题的一条重要且有效的途径.其优点是思维方式比较“固定”,学生容易掌握,突出学生平面几何的综合能力以及数学运算的素养.
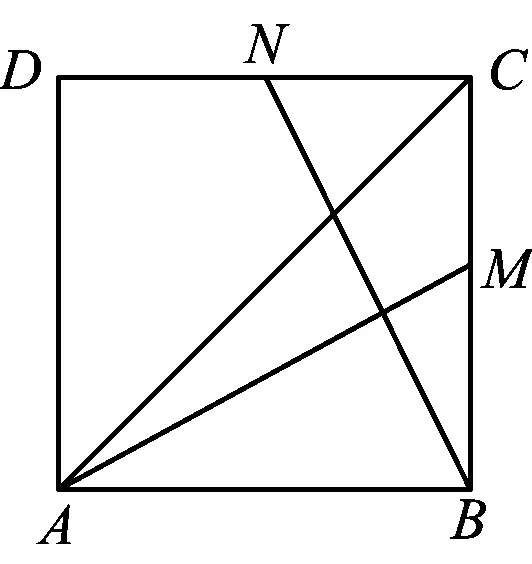
图3
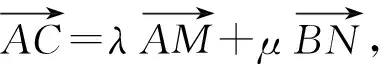
( )


分析以AB,AD为坐标轴建立平面直角坐标系,设正方形ABCD的边长为1,则
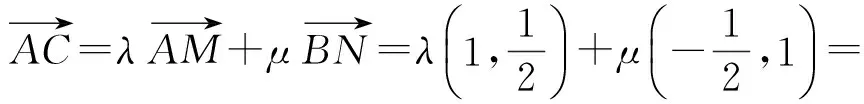
所以
解得
故
点评建系不一定基于标准状态,选择的标准都是为了构造熟悉的问题情境,从而方便后面的计算,实现解题策略的优化.
1.3 乘积运算概念化
核心概念在整个高中数学的学习中具有统领、主导的作用.学生抓住核心概念就等于抓住了高中学习的命脉;学生掌握核心概念就等于掌握了高中数学的根本.由此可见,学生解决问题的关键在于对概念的理解和掌握[2].
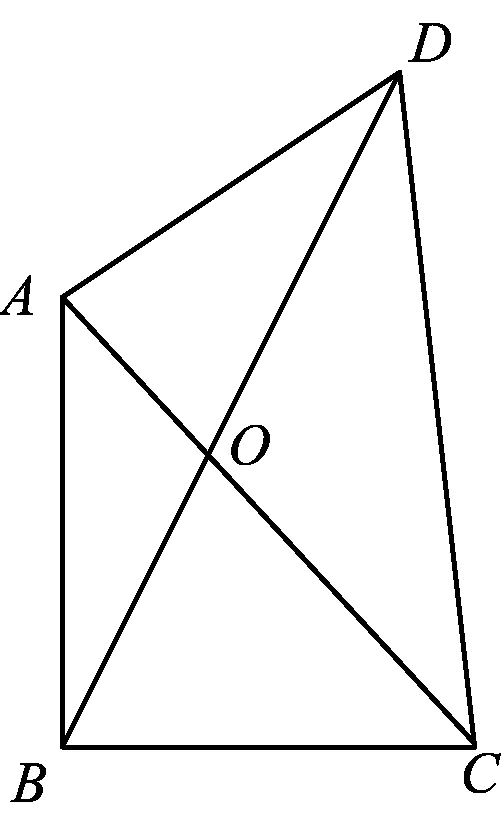
图4
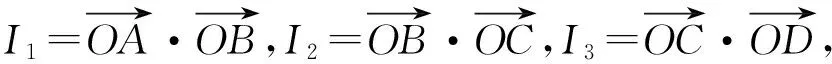
( )
A.I1 B.I1 C.I3 D.I2 (2017年浙江省数学高考试题第10题) 分析向量数量积的概念定义是 a·b=|a|·|b|cos 根据题意可判断: ∠AOB是钝角,∠BOC是锐角,从而 I1>I3, 故 I2>I1>I3. 向量的几何本质,将外在的代数关系,通过模型构造转化为熟悉的几何图形,进而将代数问题转化为相应的几何图形面积、角度、距离等的最值问题.题型简单扼要,向量的身份体现得淋漓尽致,是向量命题的常用背景. 平面向量数量积概念的两种表征体现了数量积“数”与“形”的双重身份:向量数量积的概念定义是:a·b=|a|·|b|cos 图5 通过挖掘向量的几何背景,利用数形结合的方法,对一些几何元素进行分析,避免了复杂的运算过程,既直观又形象,达到了事半功倍的效果.在构造几何图形的过程中,充分发挥了学生的空间想象力,促进了数学思想的形成. 由于向量融形、数于一体,具有几何形式与代数形式的“双重身份”,使它成为中学数学知识的一个重要的交汇点,是联系众多知识内容的媒介.因此向量成为 “在知识网络交汇处设计试题”的很好载体,从历年的高考题看,在考查平面向量的同时还将向量与函数、数列、不等式、三角和解析几何等内容相结合. 解析几何的核心思想就是利用代数方法解决几何问题.向量条件的几何形式转化为坐标形式,从而与解析几何题的常规思路接轨. 得 (a2+b2)x2-2a2cx+a2c2-a2b2=0, 即 从而 于是 a2=3b2. 点评本题虽然是解析几何中常规问题的探究,但突出了向量的数乘运算与定比分点、向量共线的关系.不难发现运用向量共线的充要条件来处理解析几何中的有关平行、共线等问题,思路清晰,且易于操作,比用斜率或定比分点来研究此类问题要简洁得多. 2017年浙江省数学高考受文理合卷的影响,解析几何大题与之前几年的考查角度变化较大,首先曲线载体选择了抛物线,更便于坐标运算,结合图像发现具有强烈的向量背景. 三角形的边角很好地展现了一个量的大小与方向,正好将平面向量与解三角形紧密联系在一起,这是考查学生问题转化能力和数形结合能力的理想平台. 图6 例6已知平面向量α,β(其中α≠0,β≠0)满足|β|=1,且α与β-α的夹角为120°,则|α|的取值范围是______. 即 向量部分最核心的是向量的加、减运算及其几何意义,也就是三角形法则、平行四边形法则以及向量的数量积定义及其几何意义.抓住这些核心,问题迎刃而解. 且 |a+b|2+|a-b|2=10, 点评此题为不等式恒成立问题和最值问题.由 |a·e|+|b·e|=|(a±b)·e|=|a±b|·|cosα|, 本题是数列和不等式的综合题,可以从数列的基本量入手,但运算会比较繁琐.若直接寻找已知和未知的关系,构造向量利用数量积的性质|a·b|≤|a|·|b|,则将大大地简化求解过程,从而体现了向量在处理综合性问题时的工具性作用. 分析由题意知 构造向量a=(3,-1),b=(an+1,a1),由|a·b|≤|a|·|b|,可知 拓展2对于任意向量a=(x1,x2),b=(y1,y2),则 |a·b|≤|a|·|b|, 即 当且仅当a∥b时,等号成立. 推广21)对于n维向量a=(x1,x2,…,xn),b=(y1,y2,…,yn),有 (x1y1+x2y2+…+xnyn)2≤ 2)对于n个向量a1,a2,…,an,有 |a1·a2·…·an|≤|a1|·|a2|·…·|an|. 平面向量是一个数学工具,更是一个数学问题的有效载体,在解决实际问题时需要合理、有效、快速地将问题进行化归转化,迅速找到问题的突破口与切入点,形成平面向量特有的数学思维方式和问题处理技巧、机制.不同的转化方式都有其优势与不足,因此在一题多解的过程中梳理不同的方法,同时更要明确最本质的解法是什么、最优的解法是什么.另外,只让学生掌握一些模式化处理问题的技巧是远远不够的,还需要伴随丰富的学习经历和经验的积累,让学生在具体问题的解决中亲历过程、直观感知、感悟策略、挖掘本质、形成思维导向,进而提升学生的数学核心素养[3]. [1] 卢明,姜巍.关注核心概念 培养核心素养[J].数学教学研究,2016,35(7):7-12. [2] 卢明.平面向量复习要强化的“5种意识”的培养[J].中学教研(数学),2014(4):1-5. [3] 华志远.透视数学核心素养,漫话课堂转型抓手——从《函数与方程》的教学实录谈起[J].数学通讯,2016(14):27-30.
2 几何背景

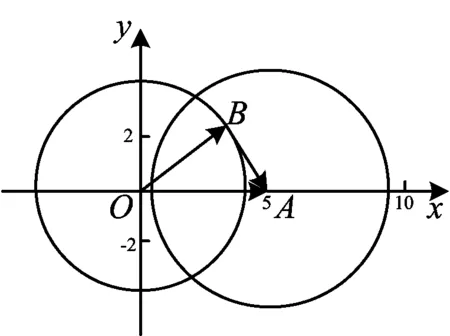

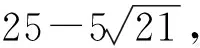
3 知识衔接多元化
3.1 平面向量与解析几何
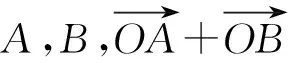
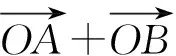
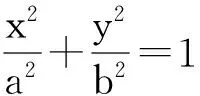
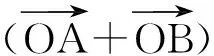


3.2 平面向量与三角函数
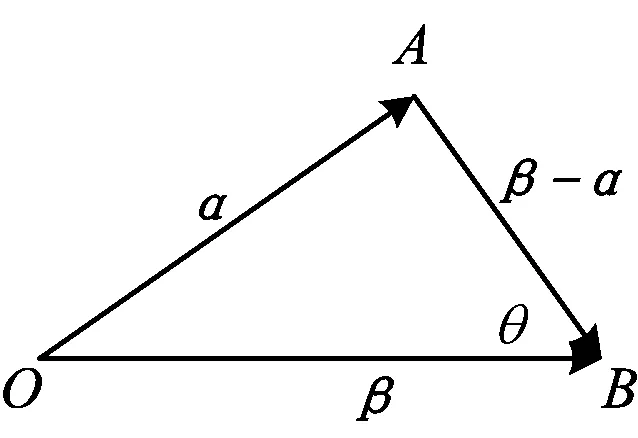
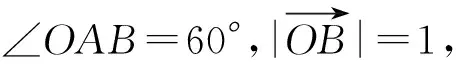
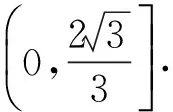
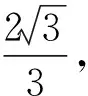
3.3 平面向量与不等式
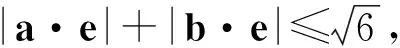
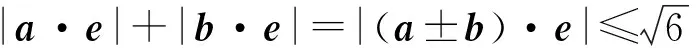
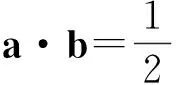
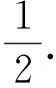
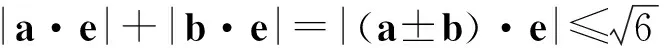

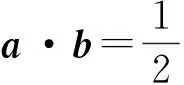
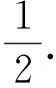
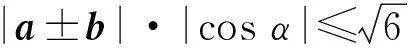
3.4 平面向量与数列