问题驱动教学实录*
——以一个不等式恒成立问题为例
●
(内江师范学院数学与信息科学学院,四川 内江 641112)
问题驱动是推进教学的重要方式,承载教师预设的教学目标,以直接的对话形式解决问题.数学问题解决是解题者在自己的长时记忆中提取解题图式用于新的问题情境的过程[1].数学教学,不仅要把“题”作为研究的对象,把“解”作为研究的目标,而且也要把“解题活动”作为对象,把学会“数学地思维”、促进“人的发展”作为目标[2].
笔者以一道不等式恒成立问题的驱动式教学为例,直观展示教师与学生的“思维对话”,暴露学生思维误区,使学生建构起知识网络,完善知识结构,细化知识组块,从而达到举一反三、触类旁通的目的.
1 问题呈现

(1987年全国数学高考试题第5题)
该高考题满分12分,以不等式恒成立为背景,涉及参数、对数、一元二次不等式,知识背景较熟悉,但是问题形式结构较复杂,从信息加工的角度来看,组块高达37个,严重超过大脑加工容量“7±2”[3]的上限,使学生望而却步.之所以选择此题进行研究:一方面,该问题是不等式经典例题中的代表,有研究价值;另一方面,当年学生的得分普遍较低,但研究发现该试题蕴含丰富的思想方法,具有较高的教学研究价值,也值得学生学习和借鉴.因此,笔者尝试采用问题驱动的形式,引导学生研究、探讨该内容.
2 实录编译
2.1 问题驱动,引发思考
师:请同学们思考,这个问题可以从哪些角度考虑?
生1:这是不等式恒成立问题,可以用判别式法,即

生(全体):没有问题.因为二次函数开口向上,Δ<0就与x轴没有交点.
(学生开始小声发表意见.)
师:这样做严谨吗?有无逻辑问题?
(学生小声讨论.)
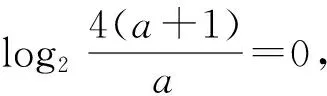

2.2 反例验证,巩固理解
师:此题对于二次项系数为0的情况无解,不影响最终答案,但是为了加深大家对讨论二次项系数的认识,我们不妨构造这样的反例进行说明:
设关于x的不等式mx2+mx+1>0恒成立,求实数m的取值范围.
生3:当m=0时,原不等式即为1>0,不等式恒成立,因此m=0是其解;当m≠0时,……
师:从这个例题看来,如果不讨论二次项系数为0的情况,这个解就容易被遗漏,也就造成逻辑的错误.因此,在处理类似的问题时,一定要注意分类讨论的标准,慎独慎思,不重不漏.
2.3 驱动探究,优化问题
师:同学们,题干中的对数形式复杂吗?可以简化吗?
生4:可以.
师:怎样简化,生4你来讲讲?

(2+log2t)x2+2(1-log2t)x+2log2t-2>0.
师:很好!形式是简单了一些,那还能再简化吗?
(全体学生开始跃跃欲试.)
生5:可以,每项都还有log2t,可以令log2t=m,原不等式进一步转化为
(2+m)x2+2x(1-m)+2(m-1)>0.
师:现在的不等式看起来简单多了.老师还想问,还能更简单吗?
生6:我知道,还可以令m-1=u,则不等式变为
(3+u)x2-2ux+2u>0.
师:同学们太棒了,把那么复杂的不等式利用换元的方法变得如此简单.这是一个关于x的一元二次不等式恒成立问题(其中3+u≠0).对于这个不等式恒成立问题,同学们可以用哪些方法解决?
(学生思考,做题.)
师:请同学们来展示一下自己的方法.
生7:用判别式法:若3+u=0,则无解;若3+u≠0,则原不等式为关于x的一元二次不等式,只需满足
解得u>0,于是得到0 生8:可以用分离参数法.不等式左边可以看作u的一次函数,不等式可以变为 u(x2-2x+2)+3x2>0, 即 师:分离参数的方法非常好,那么什么时候能用分离参数法? 生8:是关于u的一次数函数时. 师:关于u的二次函数呢? 生8:可以,只要u的次数一样. 师:对于这个问题,我们发现其问题实质就是 (3+u)x2-2ux+2u>0, 师:生9直接把x的范围限定了,那么使用判别式法就要谨慎,分离参数法同样奏效.非常好! 师:生10不仅将x的范围限定了,还将一个对数结构改变了,其本质改变了吗? 生11:没有,只是要借用换底公式. 师:对,这也是一个非常好的变式. 师:这是一个有难度的变式,又增加了一个参数k,请同学们寻找答案. 波利亚曾指出,回顾已经完成的解答是解题工作中的一个重要且有启发性的阶段[4].回顾本堂课,教师采用不断追问的方式,一步步引领学生优化解题方法,逐层深入解决问题,并以此为跳板,进一步激发学生对一类问题的认识,开拓学生的思维宽度,这不仅培养了学生的逻辑推理能力,还挖掘了学生的数学应用意识与创新意识.这堂问题驱动式教学课是师生共同参与的教学活动,学生经历了发现问题、分析问题、解决问题的过程,进一步对问题进行改编、延伸甚至推广.回顾问题解决的过程,有以下3点值得思考. 从这个不等式恒成立问题来看,通过分析找到了命题根源(3+u)x2-2ux+2u>0.教师引导学生对问题抽丝剥茧,经历了3次换元过程,引进了t,m,u这3个参数,充分体现了学生整体化、数学化、符号化的意识,进一步让学生认识到换元有简化问题的作用.其中对本原问题的参数u进行替换还可以衍生出不同类型复杂的问题,包括对数、三角、数列等等,但问题的实质始终如一. 当x的范围改变时,判别式法的使用也受限制,更一般的是分离参数法.而分离参数的使用条件必须满足参数齐次性,即参数的次数保持一致,否则该方法也难以奏效. 受罗增儒信息论观点[2]下的证明框架的启示,本节课教师引导学生对问题解决的整体过程可用如图1表示. 图1 此框图有利于学生形成解题分析的思路框架,有利于学生从整体上把握解题概况.一方面数学是一门逻辑科学,需要学生一步步建立思路流程图;另一方面,数学知识之间相互交叉,需要学生进一步从整体把握知识信息网. [1] 王凯.数学解题认知模式下的数学解题教学[J].中学数学月刊,2014(5):11-13,30. [2] 罗增儒,罗新兵.作为数学教育任务的数学解题[J].数学教育学报,2005,14(1):12-15. [3] George A M .The Magical Number Seven,Plus or Minus Two:Some Limits on Our Capacity for Processing Information[J].Psychological Review,1956(63):81-97. [4] 波利亚.数学的发现——对解题的理解、研究和讲授(第一卷)[M].欧阳绛,译.北京:科学出版社,1982.
2.4 横向迁移,引导思考

2.5 问题推广,发散思维
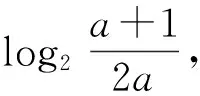
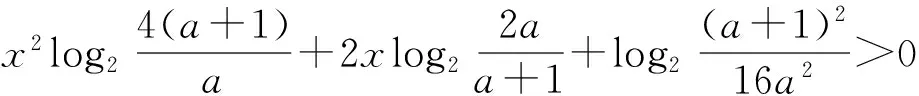
3 回顾与反思
3.1 问题本质认识
3.2 方法使用条件
3.3 思路分析框图