基于正则渐进迭代逼近的自适应B样条曲线拟合

刘明增，郭庆杰，王思奇



基于正则渐进迭代逼近的自适应B样条曲线拟合

刘明增，郭庆杰，王思奇

(大连理工大学盘锦校区基础教学部，辽宁 盘锦 124221)

基于渐进迭代逼近(PIA)的数据拟合方法以其简单和灵活的特性获得了广泛的关注。为了获得高保真度的拟合曲线，提出了一种基于主导点选取和正则渐进迭代逼近(RPIA)的自适应B样条曲线拟合算法。首先根据数据点的曲率估计选取初始主导点并生成初始PIA曲线。然后，借助于拟合误差和数据点集的曲率分布选取加细的主导点及实现PIA曲线的更新。得益于基于曲率分布的主导点选取，使得拟合曲线在复杂区域分布较多的控制顶点，而在平坦区域则较少。通过正则参数的引入构造了一种RPIA格式，提升了渐进迭代控制的灵活性。最后，数值算例表明相比于传统最小二乘曲线拟合该算法在使用较少数量的控制顶点时可实现较高的拟合精度。

B样条曲线拟合；正则渐进迭代逼近；自适应加细；曲率估计

给定数据点的B样条曲线拟合在计算机图形学、CAD/CAM和计算机视觉等许多领域是经常遇到的一个问题[1-4]。标准的B样条曲线拟合通常要进行数据点的参数化，然后建立以B样条曲线控制顶点为未知量的一个优化问题，继而转化为求解相应的线性方程组[1,4]。

最近，一种不需要求解线性方程组且具有明显几何意义的渐进迭代逼近(progressive iterative approximation，PIA)方法获得了大量的关注[5]。其主要利用混合基函数的PIA性质：构造一条初始拟合曲线，通过逐次迭代调整其控制顶点使得该拟合曲线插值或逼近给定的数据点集。齐东旭等[6]提出了均匀3次B样条具有上述的PIA性质。LIN等[7-8]进一步推广上述结果到非均匀3次B样条曲线，并首次提出了英文术语progressive iterative approximation。文献[9]指出有理非均匀B样条(non-uniform rational B-Splines，NURBS)曲线曲面也具有上述的PIA性质。此外，LIN和ZHANG[10]提出一种用于拟合大规模数据点的EPIA(extended PIA)算法，该算法允许控制顶点数目少于数据点数。LIN[11]提出一种在每次迭代中可部分调整控制顶点的局部PIA算法。文献[12-13]通过在迭代步中引入权重因子进而提升了PIA算法的效率。针对在PIA方法中每次迭代中数据点的参数值固定不变问题，MAEKAWA等[14]提出将数据点的参数值更新为每次迭代曲线上最近点的参数值并称之为几何插值法。近来，DENG和LIN[15]提出一种新的PIA算法，该算法的极限曲线或曲面等价于给定数据点的最小二乘拟合结果。

得益于B样条曲线的局部支集性质，可认为每个控制顶点都支配着待表示物体的部分几何信息。显然，事先无法知道需要多少控制顶点在满足指定精度的前提下来表达物体。在本文中，将考虑如何在保持拟合精度的前提下，减少B样条曲线的控制顶点数目以期减少冗余控制顶点的信息。YANG等[2]基于SDM(squared distance minimization)优化提出了一种自动调整控制定点数据的算法，但该算法对初始B样条曲线过于敏感。在拟合问题中，一些点会对拟合曲线的精度产生决定性的影响。基于这种观察，PARK[4]提出了一种基于主导点(dominant point)选取的自适应B样条曲线拟合算法，但在该算法每次迭代中需要求解一个线性方程组，且随着迭代的进行方程组的规模也逐步增长。文献[16]提出一种约束曲线在曲面上的基于主导点选取的自适应保形曲线拟合算法。本文拟基于数据点的几何信息(如曲率)获取初始曲线的控制顶点。而后，采用渐进迭代近似实现数据点集的拟合，继而避免了求解线性方程组。鉴于此，提出一种基于正则渐进迭代逼近(regularized progressive iterative approximation, RPIA)的自适应B样条曲线拟合算法，该算法采用基于主导点选取的曲线加细技术来保证拟合曲线的精度。

1 基于正则渐进迭代的自适应拟合算法

PIA方法是一种具有明显几何意义的几何迭代方法，通过迭代调整曲线的控制顶点得到最后拟合给定点集的逼近曲线[7-13,15]。尽管PIA方法的初始控制顶点可以任意指定，合理选取初始曲线的控制顶点对极限曲线的生成质量有极其重要的影响[15]。

综上，为避免求解线性方程组，本文采用PIA方法拟合给定的数据点集。同时，考虑结合数据点集曲率信息来进行初始控制顶点的选取，且在迭代格式中引入一个正则自由度来增加PIA的灵活性。本文算法流程概括如下：首先通过估计数据点的曲率信息获取初始的主导点集，继而生成首次RPIA曲线；然后，结合迭代曲线的拟合误差和数据点曲率信息增选相应的主导点；最后，更新RPIA曲线直到满足指定的拟合精度。本文算法由4部分组成：数据点的参数化、主导点的初始选取和更新、节点向量的配置及更新和RPIA曲线的生成。图1展示了人脸轮廓数据的自适应B样条拟合示例。

1.1 数据点的参数化

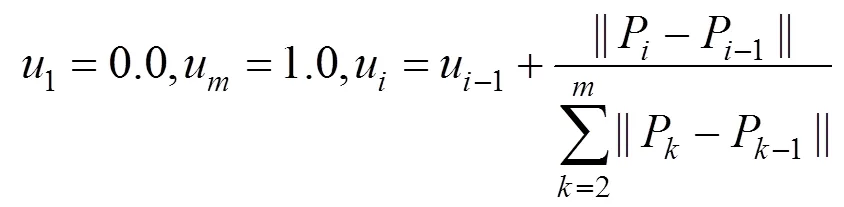
1.2 主导点的初始选取及节点向量的配置

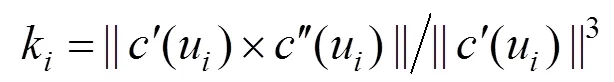
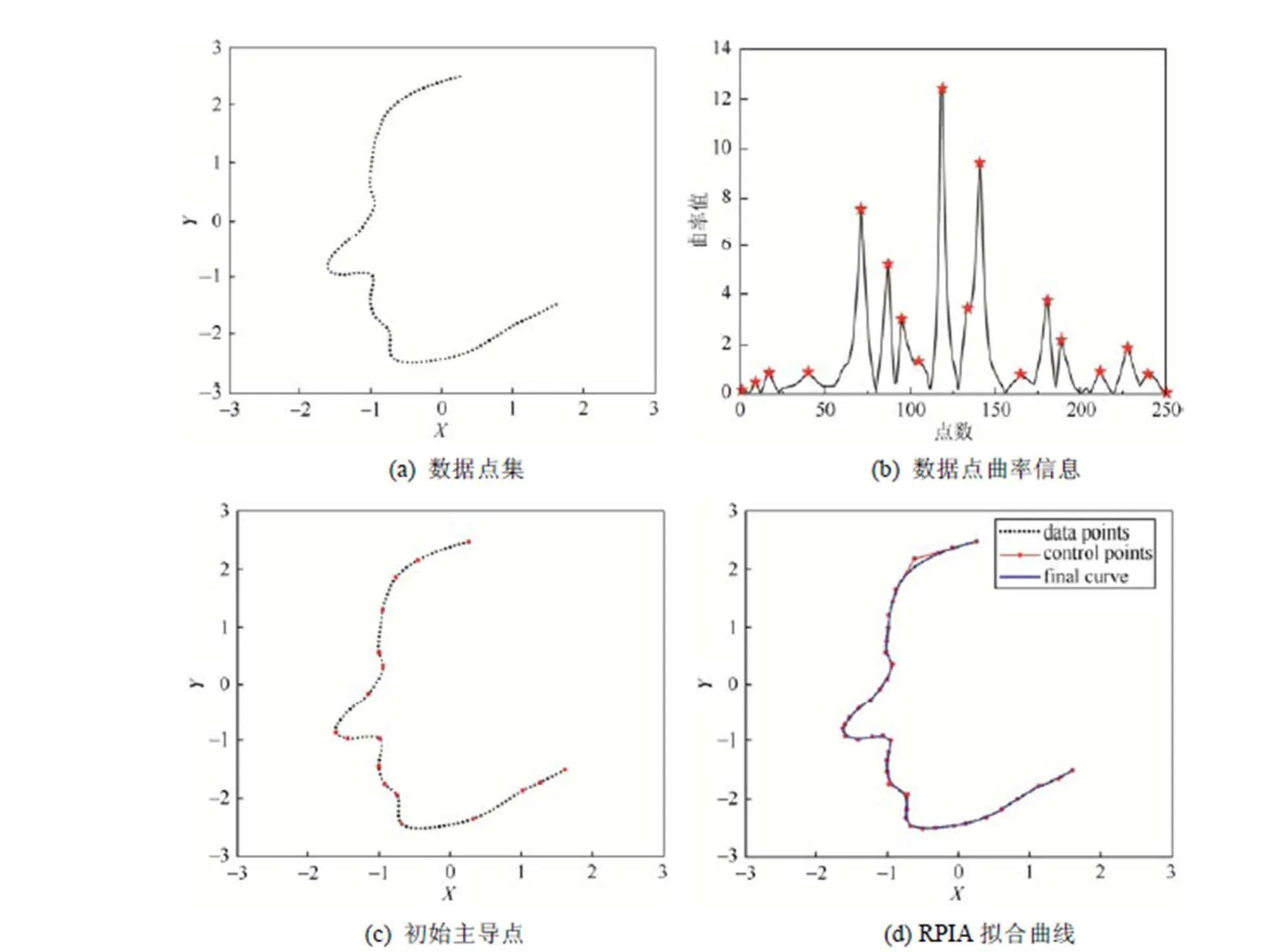
图1 人脸轮廓数据的B样条曲线拟合示例

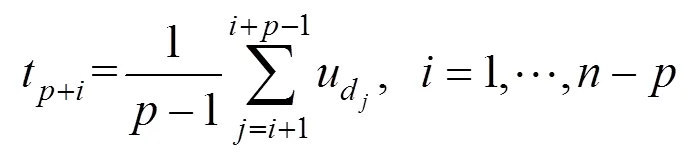
1.3 主导点及节点向量的更新

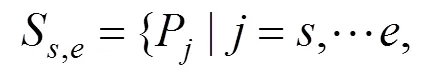
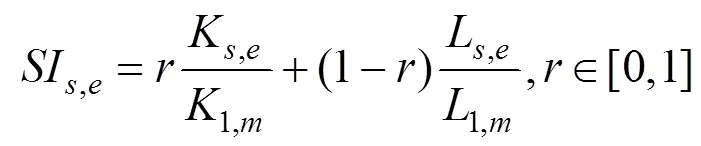
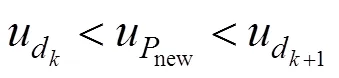
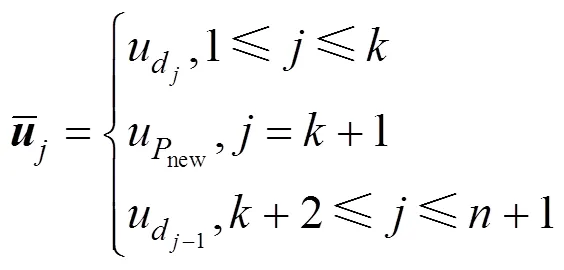
于是，更新后主导点集形成的内部节点向 量为

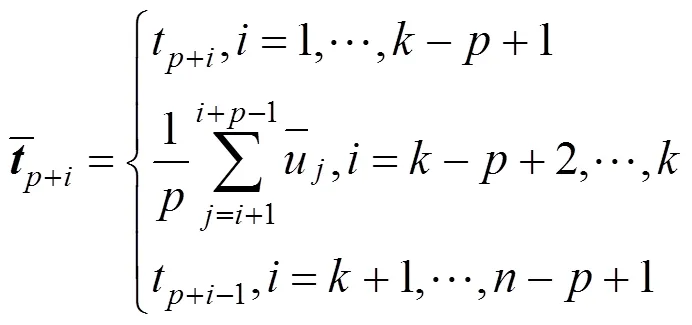
从式(4)易知，只需对式(2)中的节点向量进行部分更新即可。

1.4 正则渐进迭代逼近曲线的生成

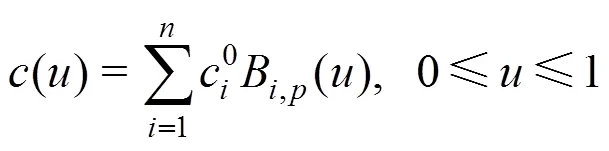
记相应基函数的配置矩阵为

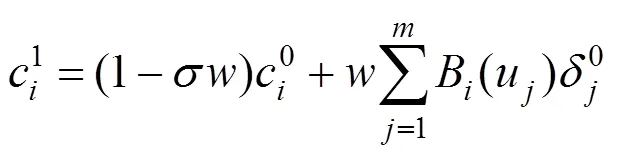
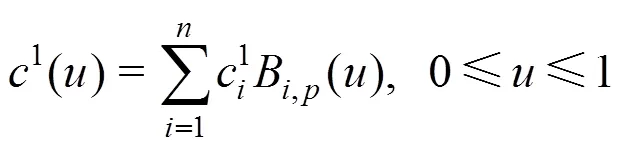
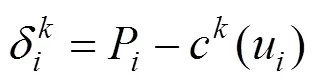
则第+1次迭代曲线为

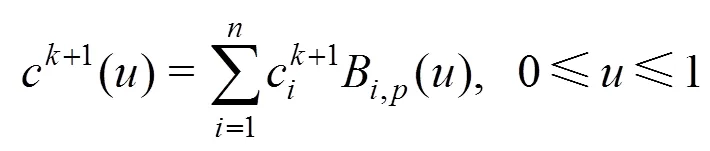
整理式(8)可得

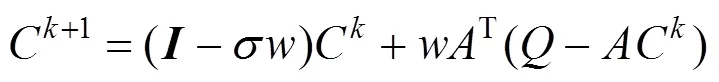
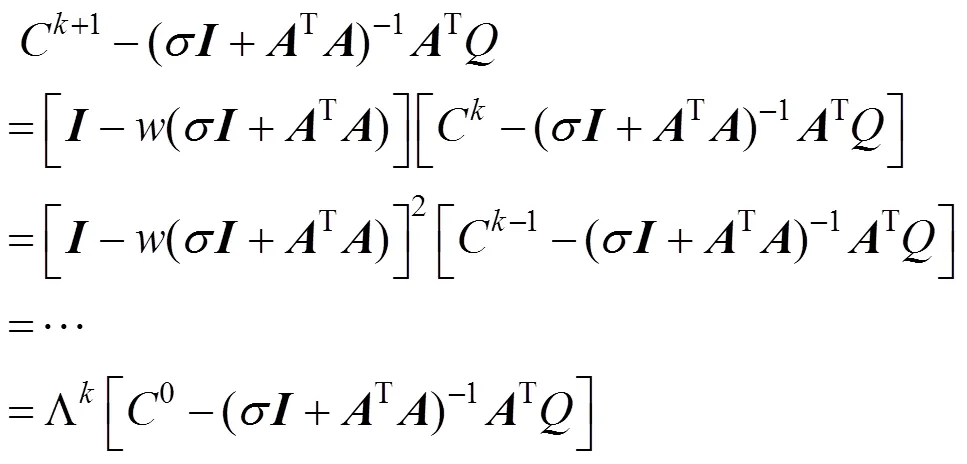
根据式(11)可得

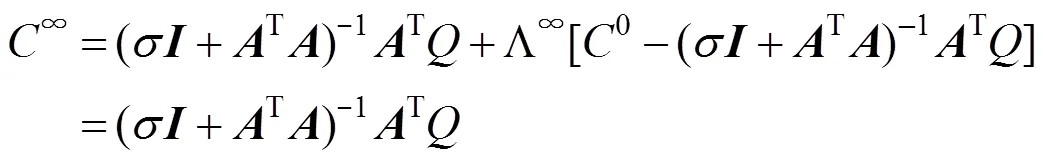
1.5 算法流程

本文算法流程如下：

（4）德城区建成区的扩展主要受人口、经济、交通和政策4个因素综合影响．其中，政策因素成为主导城市发展的最重要驱动力．

步骤4.1. RPIA拟合曲线c()。

步骤4.2.选取加细区S,e和新的主导点new=new。

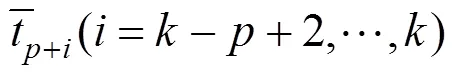
步骤4.4.如果满足指定拟合误差结束循环。

2 数值算例

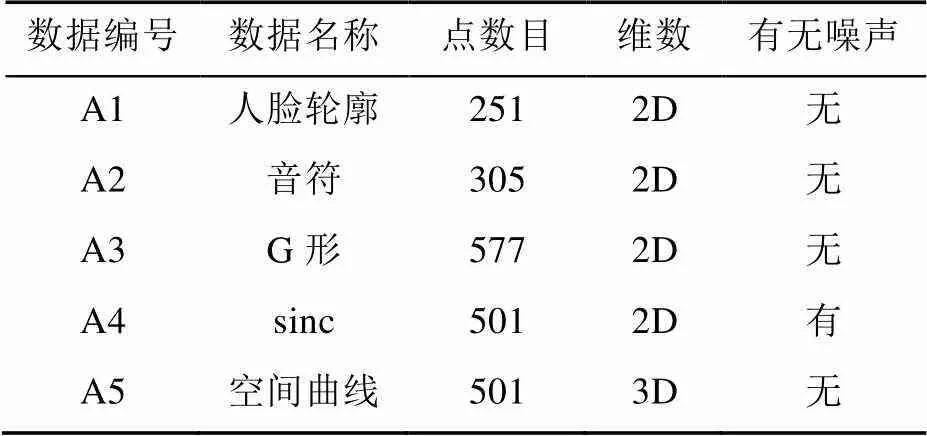
表1 数据点集统计信息

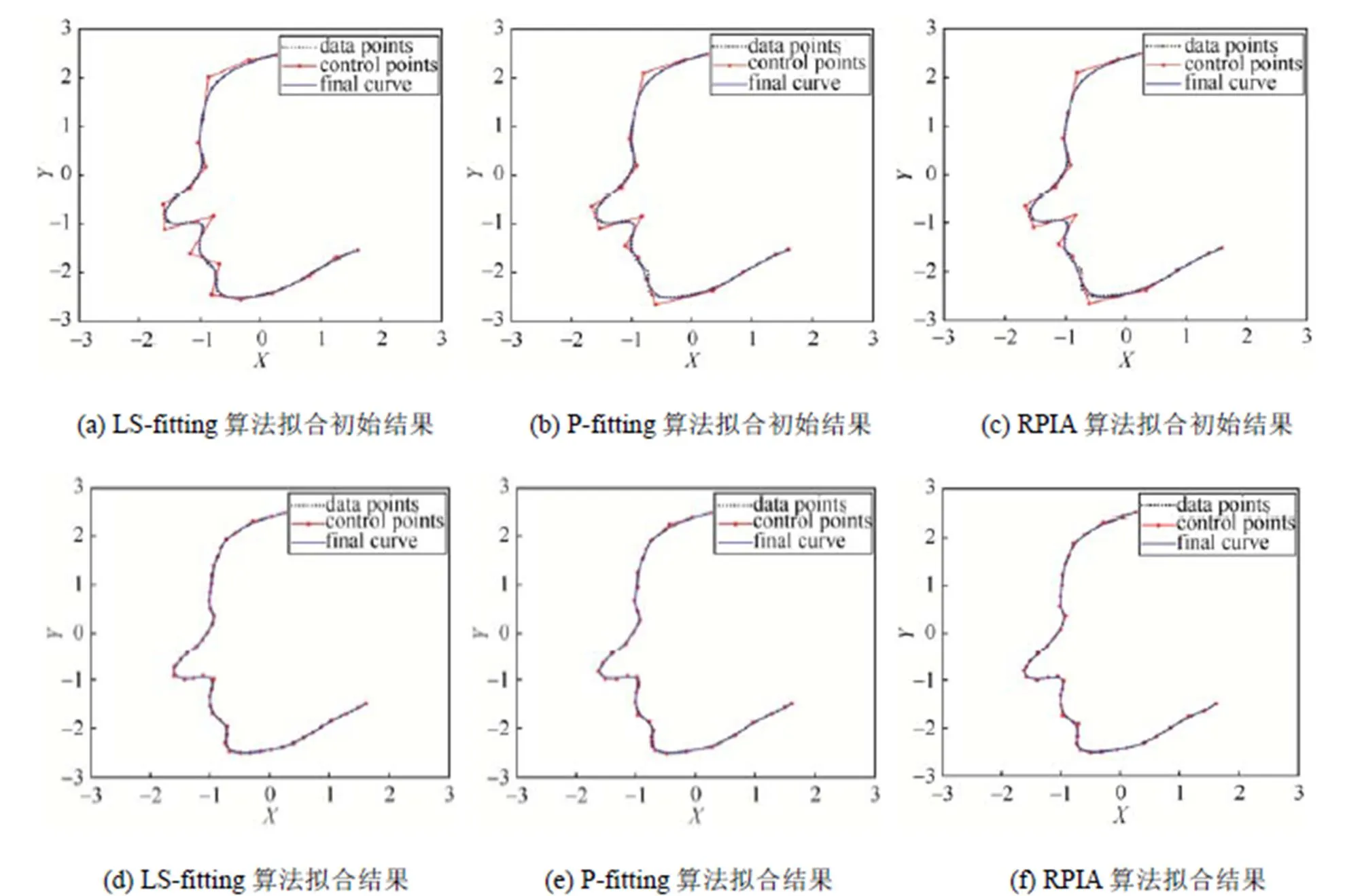
图2 A1数据的曲线拟合结果

表2 图2最大误差信息

图3对比分析了A1人脸轮廓数据在本文RPIA方法、LS-Fitting算法和P-fitting算法的拟合效率信息。由图3(a)可知，在指定相同的拟合误差标准时，RPIA方法需要较少的控制顶点数目，即一定程度上是减少了冗余控制顶点信息。由图3(b)可知，在控制顶点数目相同时，RPIA拟合可以达到较小的拟合误差。

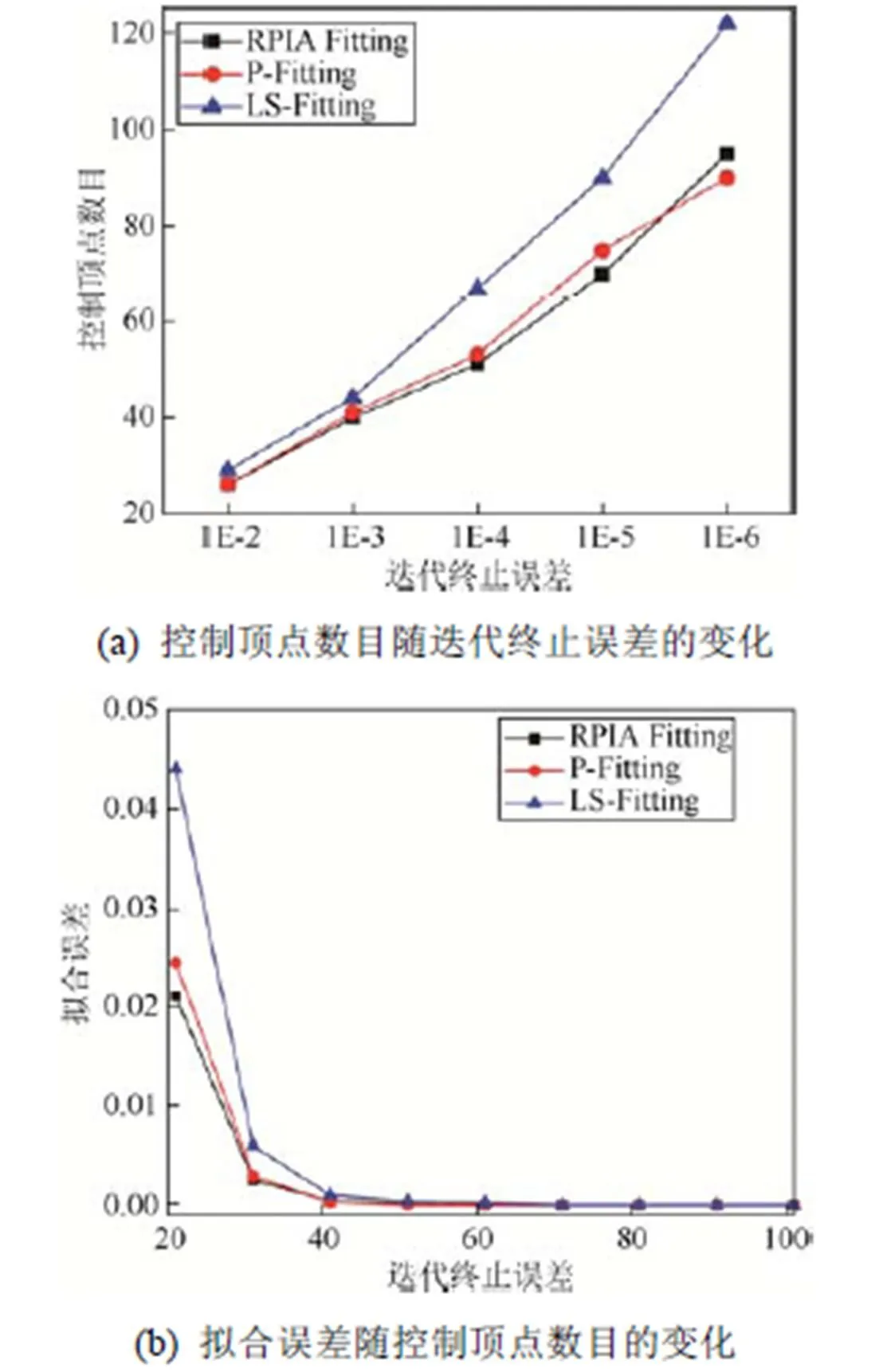
图3 A1人脸轮廓数据的拟合效率分析

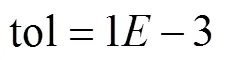
图4 A2音符数据RPIA拟合曲线及拟合效率分析

图6为带噪声平面曲线拟合结果(A4数据集)和3D空间曲线(A5数据集)拟合结果。表4列出了图5中数据点集的误差信息。

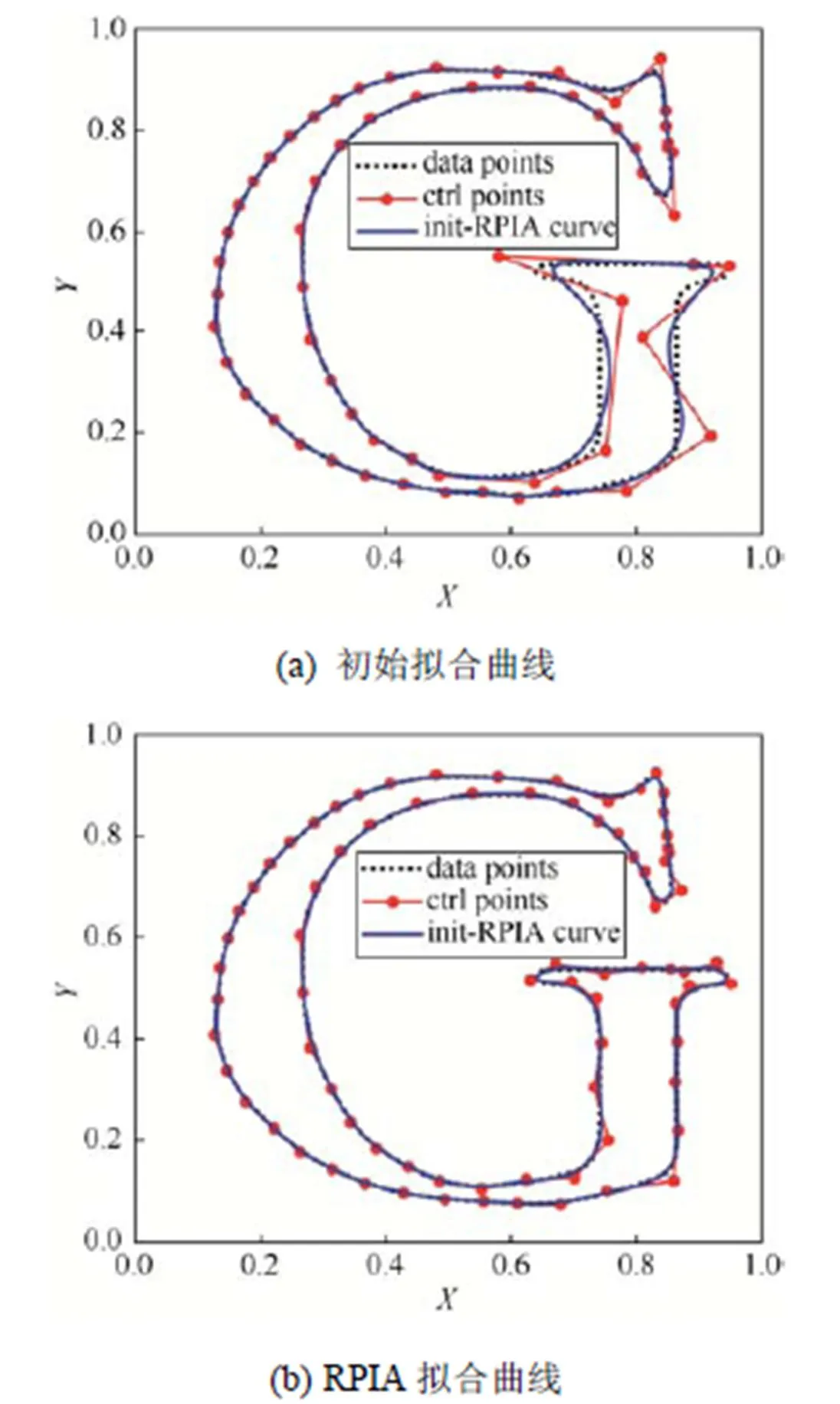
表3 不同控制顶点数目(21,31,41,51,61,71)时的最大误差

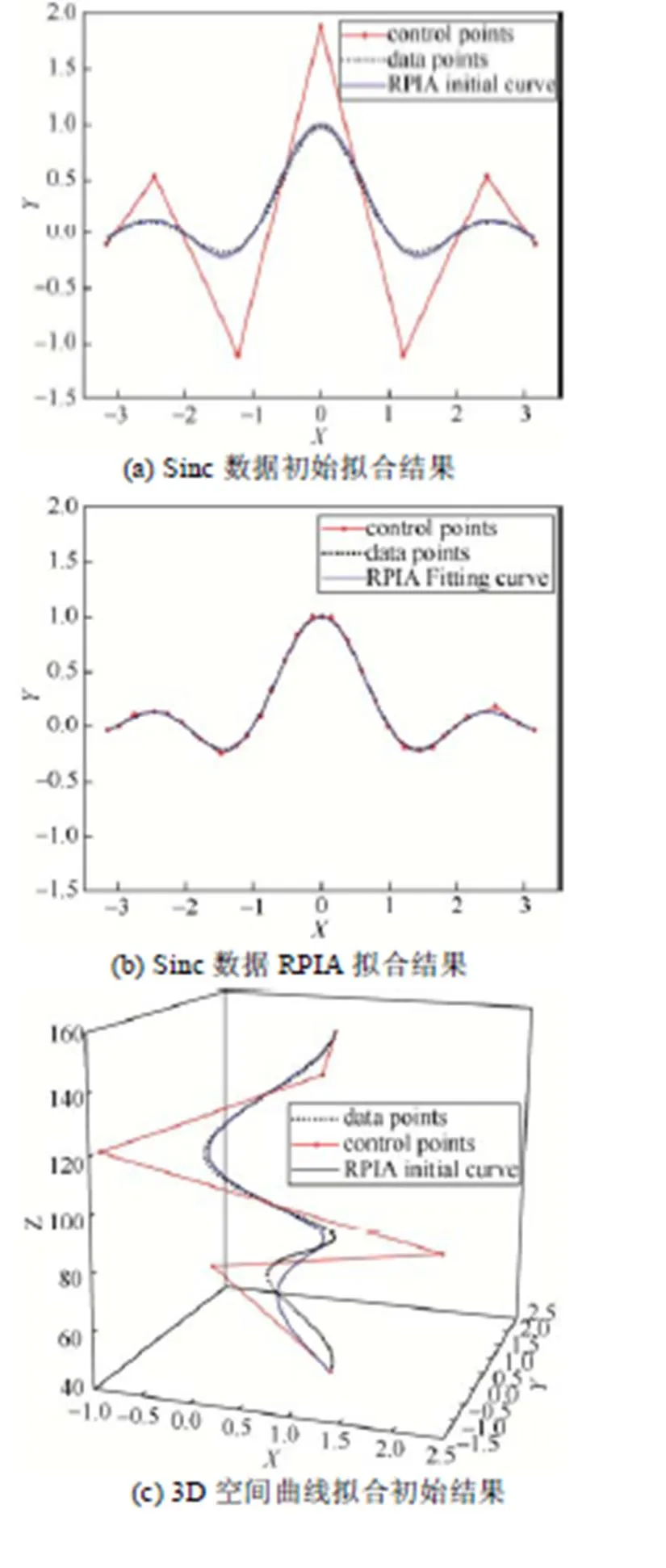
表4 图6最大误差信息

3 结束语

本文提出了一种基于RPIA的曲线拟合方法，结合主导点的选取实现了拟合的自适应。通过数值算例验证可知，与传统的最小二乘拟合方法相比，在指定拟合误差时，本文方法只需较少的控制顶点，而在指定相同控制顶点数目时，具有更小拟合误差。由于PIA格式的引入避免了传统拟合方法中求解线性方程组的问题，提高了求解效率。但本文中也有一些不足之处，本文算法中涉及到B样条曲线的节点删除操作，会导致删除后B样条曲线的误差增大，继而增大迭代步数。

[1] PIEGL L, TILLER W. The NURBS book [M]. 2th ed. New York: Springer, 1997: 410-419.

[2] YANG H P, WANG W P, SUN J G. Control point adjustment for B-spline approximation [J]. Comuter-Aided Design, 2004, 36(7): 639-652.

[3] WANG W P, POTTMANN H, LIU Y. Fitting B-spline curves to point clouds by curvature-based squared distance minimization [J]. ACM Transactions Graphics, 2006, 25(2): 214-238.

[4] PARK H. An error-bound approximation method for representing planar curves in B-splines [J]. Computer-Aided Design, 2004, 21(5): 479-497.

[5] 蔺宏伟. 几何迭代法及其应用综述[J]. 计算机辅助设计与图形学学报, 2015, 27(4): 582-589.

[6] 齐东旭, 田自贤, 张玉心, 等. 曲线拟合的数值磨光方法[J]. 数学学报, 1975, 18(3): 173-184.

[7] LIN H W, WANG G J, DONG C S. Constructing iterative non-uniform B-spline curve and surface to fit data points [J]. Science in China, Series F, 2004, 47(3): 315-331.

[8] LIN H W, BAO H J, WANG G J. Totally positive bases and progressive iteration [J]. Computers and Mathematics with Applications, 2005, 50(3/4): 575-586.

[9] 史利民, 王仁宏. NURBS曲线曲面拟合数据点的迭代算法[J]. 数学研究及应用, 2016, 26(4): 735-743.

[10] LIN H W, ZHANG Z Y. An extended iterative format for the progressive-iterative approximation [J]. Computer & Graphics, 2011, 35(5): 967-975.

[11] LIN H W. Local progressive-iterative approximation format for blending curves and patches [J]. Computer Aided Geometric Design, 2010, 27(4): 322-339.

[12] LU L Z. Weighted progressive iteration approximation and convergence analysis [J]. Computer Aided Geometric Design, 2010, 27(2): 129-137.

[13] ZHANG L, GE X Y, TAN J Q. Least square geometric iterative fitting method for generalized B-spline curves with two different kinds of weights [J]. Visual Computer, 2016, 32(9): 1109-1120.

[14] MAEKAWA T, MATSUMOTO Y, NAMIJI K. Interpolation by geometric algorithm [J]. Computer-Aided Design, 2007, 39(4): 313-323.

[15] DENG C Y, LIN H W. Progressive and iterative approximation for least squares B-spline curve and surface fitting [J]. Computer-Aided Design, 2014, 47: 32-44.

[16] HU P, LIU M Z, LI B J, et al. Adaptive shape-preserving curve fitting on surfaces [J]. Journal of Information & Computational Science, 2012, 9(1): 15-23.

[17] PARK H, LEE J. B-spline curve fitting based on adaptive curve refinement using dominant points [J]. Computer-Aided Design, 2007, 39(6): 439-451.

Adaptive B-spline Curve Fitting Based on Regularized Progressive Iterative Approximation

LIU Mingzeng, GUO Qingjie, WANG Siqi

(School of Mathematics and Physics Science, Dalian University of Technology, Panjin Liaoning 124221, China)

The use of progressive iterative approximation (PIA) to fit data points has received a deal of attention benefitting from its simplicity and flexibility.To obtain a fitting curve satisfying the shape high fidelity, we present an adaptive B-spline curve fitting algorithm based on regularized progressive iterative approximation (RPIA) and the selection of dominant points. Firstly, the initial dominant points are selected from the given points in terms of curvature estimates and an initial progressive iterative approximation curve is constructed. Then the fitting curve based on RPIA is updated by means of the fitting error and the selection of refinement dominant points according to the curvature distribution of given points. The fitting curve possesses fewer control points at flat regions but more at complex regions. By the use of a regular parameter, progressive iterative approximation is generalized and the flexibility of PIA is promoted. Finally, numerical examples are provided to demonstrate that compared with the conventional least square approaches the proposed method can achieve a higher fitting precision with far fewer control points.

B-spline curve fitting; regularized progressive iterative approximation; adaptive refinement; curvature estimation

TP 391

10.11996/JG.j.2095-302X.2018020287

A

2095-302X(2018)02-0287-08

2017-07-13；

2017-08-28

国家自然科学基金项目(11601064)；中央高校基本科研业务专项资金项目(DUT14RC(3)024，DUT16RC(4)67，DUT17LK09)

刘明增(1984–)，男，河南淮阳人，讲师，博士。主要研究方向为计算几何、计算机图形学。E-mail：mzliu@dlut.edu.cn