一种新的图像去模糊清晰化方法

王文豪，严云洋，姜明新，于永涛，赵文东



一种新的图像去模糊清晰化方法

王文豪，严云洋，姜明新，于永涛，赵文东

(淮阴工学院计算机与软件工程学院，江苏 淮安 223003)

针对在实际环境中很难得到图像去模糊所需要的大量先验知识，诸如退化模式、点扩散函数等，提出了一种新的图像去模糊清晰化方法。首先利用高斯差分算子获得图像轮廓信息，然后根据轮廓信息预测清晰图像过渡区，再利用清晰图像过渡区、退化图像和点扩散函数之间的关系建立目标函数，为了克服噪声的影响，在目标函数中加入了非负性惩罚项和空间相关性约束项，并使用滞后迭代的极小化方法来求解点扩散函数；最后通过已有的非盲目图像复原算法复原图像。实验结果表明，该方法无需知道图像退化模式，对各种因素引起的退化图像都能有效地复原。

图像去模糊；清晰化；过渡区；点扩散函数

图像在获取、传输和保存过程中，由于目标运动、大气扰动、对焦不准、散射等各种因素的影响，会导致图像退化，出现模糊、细节丢失的情况，使得目标无法识别[1-2]。图像复原技术是解决此类问题非常有效的手段。图像复原技术按照是否需要点扩散函数可分为非盲目图像复原和盲目图像复原，非盲目图像复原需要在点扩散函数已知的情况下对图像复原，而盲目图像复原是在点扩散函数未知的情况下直接对图像复原。

在非盲目图像复原方法中主要有维纳滤波算法[3-4]、最大熵复原算法[5]和Richardson- Lucy(R-L)复原方法[6]，其中R-L方法应用较广泛，其是一种基于泊松分布的最大似然图像复原算法，通过迭代求解原始清晰图像，但该方法对噪声具有放大的缺陷。针对此问题，很多学者对R-L算法进行了改进，李勇等[7]提出了阻尼R-L算法，通过修正似然函数，以减少噪声的影响。YUAN等[8]提出一种基于双边R-L的多尺度细化方法。这些方法在实际应用中虽然取得一定的效果，但需要事先知道点扩散函数，由于引起图像退化因素很多，且在实际环境中点扩散函数往往是未知的，因而这类方法的使用受到很大限制。于是人们开始转向盲目图像复原[9]。AYERS和DAINTY[10]提出迭代盲目去卷积方法(iterative blind deconvolution, IBD)，该方法利用点扩散函数的非负性和真实图像估计的约束，使用快速傅立叶变换，在时域和频域上交替迭代来还原图像，该方法运算时间复杂度较高，对初始值较敏感，不够稳定。TV复原算法引入了正则化思想，通过抑制图像的梯度变化的总和来复原图像[11-12]。该方法能在一定程度上保护图像细节，主要适用于分片光滑的图像，对于不满足此要求的图像，复原结果不够好。NAS-RIF复原算法[13]将估计图像投影到支撑域，通过计算投影图像和估计图像之间的误差大小来评判点扩散函数，该方法对散焦模糊的退化图像复原较好，对运动模糊及其他复杂退化图像复原不够好。FERGUS等[14]复原算法利用图像梯度的“拖尾分布”作为先验知识，并通过混合高斯模型拟合此分布，该方法对相机抖动这类运动模糊图像可以取得较好的效果，对其他类型的退化图像复原结果较差。上述各种盲目复原方法仅对特定图像退化模式有效，对不同退化模式的图像需使用不同的复原方法。在实际应用中图像退化通常是由多种因素综合造成的，含有多种退化模式，各种退化模式对目标图像的退化影响程度也是各不相同的，如果只考虑单一因素，忽略其他因素的影响，势必会影响图像的复原结果。

基于以上分析，本文提出了一种新的图像去模糊清晰化方法，该方法利用模糊图像的轮廓来预测清晰图像过渡区，再根据清晰图像过渡区、退化图像和点扩散函数之间的关系建立目标函数，在目标函数中加入了非负性约束项和空间相关性约束项以抑制噪声的影响，最后通过已有的非盲目图像复原算法来复原图像。该方法优点是不需要知道图像退化模式，对任何因素造成的模糊图像都可以复原。

1 图像退化数学模型

图像退化原因多种多样，主要包括空间退化和点退化两种类型。空间退化主要是由于电子元件的失常、图像传感器与目标之间的相对运动、对焦不准、大气湍流等原因造成的。点退化通常指噪声，产生于电子元件和图像数字化过程中。图像的退化过程如图1所示。其中，(,)为未退化的清晰图像；(,)为模糊核(即点扩散函数)；(,)为各种类型噪声(主要包括高斯噪声和椒盐噪声)；(,)为退化图像。

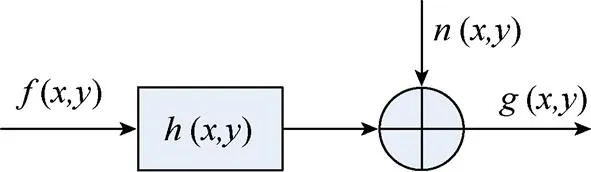
图1 图像退化模型

用数学式描述为

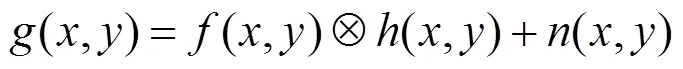
2 图像去模糊清晰化算法

退化图像可以分成背景区、目标区和两者之间的过渡区(轮廓周围区域)，背景区和目标区比较平坦，包含的退化信息比较少，图像退化信息主要隐藏在过渡区中。不同的退化模式，过渡区的变化是不一样的，同一退化模式，退化越严重，过渡区变化也越大，清晰图像被模糊后，其过渡区域的位置没有发生改变[15]。因此，可以利用过渡区主要信息空间分布的变化来复原图像。基于此本文提出了一种图像去模糊清晰化的方法，具体流程如图2所示。首先利用高斯差分算子获得模糊图像轮廓信息，然后利用模糊图像轮廓信息预测清晰图像过渡区，再利用清晰图像过渡区、退化图像和点扩散函数之间的关系建立目标函数，并求解点扩散函数，最后通过非盲目图像复原算法来复原图像。

图2 图像去模糊清晰化流程

2.1 模糊图像轮廓检测

图像中轮廓属于高频区域，本文利用高斯差分算子(difference of Gaussian, DoG)检测模糊图像轮廓，其数学式为

其中，和是高斯滤波器方差。DoG算子与图像做卷积运算，结果会得到一条波峰到波谷的曲线，如图3所示，过零点处为图像的轮廓位置，利用这一特性来提取模糊图像轮廓。为了保证过渡区信息的有效性，本文不提取所有的过渡区，只提取明显的主要过渡区，因此，需要有一个指标来度量过渡区。为此本文提出轮廓测度的概念，利用轮廓测度来选择主要的过渡区。本文将轮廓测度定义为图3中从波峰到波谷的距离p，因此可以利用p值控制轮廓强度，提取出所需的主要轮廓。

2.2 清晰图像过渡区预测

图像被模糊后，图像轮廓的位置并没有改变，改变的只是轮廓区域像素灰度值的空间分布。因此可以通过定位模糊图像轮廓位置来预测清晰图像过渡区。具体方法如下：

(1) 沿着轮廓，在轮廓垂直方向上寻找像素灰度值的上限值和下限值，将所有搜索过的区域作为模糊图像过渡区。因为只有轮廓附近的值是可靠的，所以只使用轮廓两侧附近区域(即过渡区)作为有效区域，如图4所示。

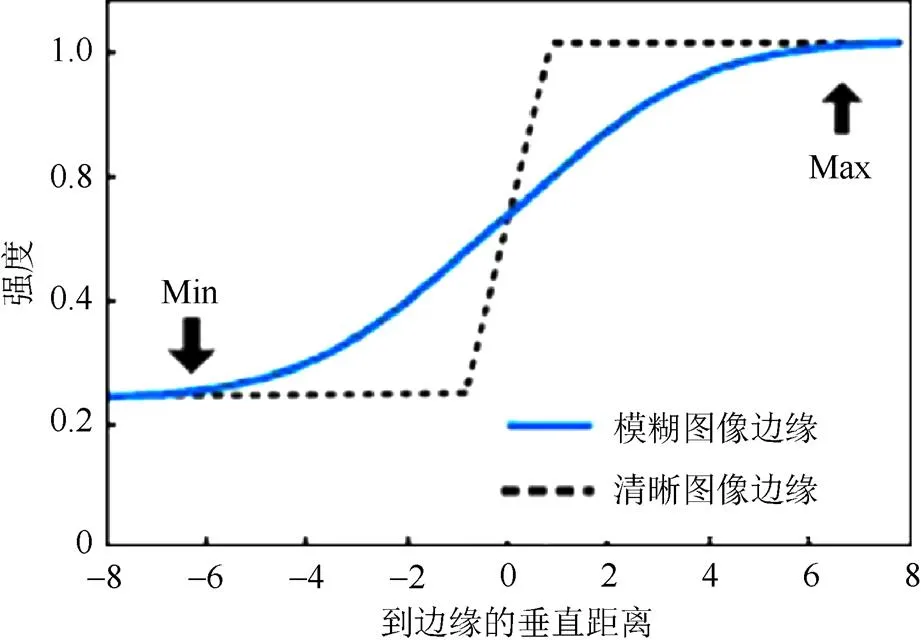
图4 过渡区预测

(2) 搜索到模糊图像过渡区域后，向此区域填充特定的值以达到预测清晰图像过渡区的目的。具体方法如下：

①对处于轮廓上的像素用最大值和最小值的平均加权来填充，加权值依据像素所在位置到中心像素的距离来确定。

②对最大值区域用对应的最大值填充，最小值区域用对应的最小值填充。

③若出现填充不完全的现象，进行插值以保证轮廓线两侧区域填充完全。

2.3 点扩散函数——求解模型

由式(1)可知，在预测到清晰图像过渡区后，根据退化图像可以求解出点扩散函数，一旦得到点扩散函数，就可用现有的非盲目复原方法来复原图像。因此如何从三者关系模型中求解出较准确的点扩散函数是关键。

无噪声时，预测的清晰图像过渡区、原退化图像、点扩散函数三者的关系可以表示为

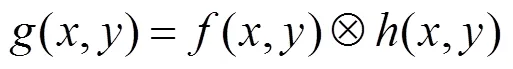
其离散形式如下

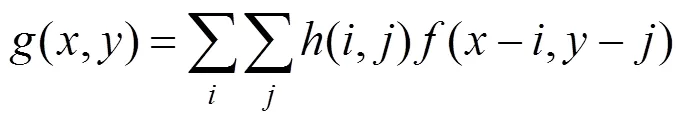
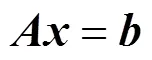
在实际环境中，噪声的影响是不可避免的，其对实际图像的估计会造成很大的影响，为了削弱噪声的影响，提高复原算法的稳定性，可加入非负性约束条件；同时为了保证点扩散函数相邻点之间的光滑性，加入空间相关性约束，其目标函数如下

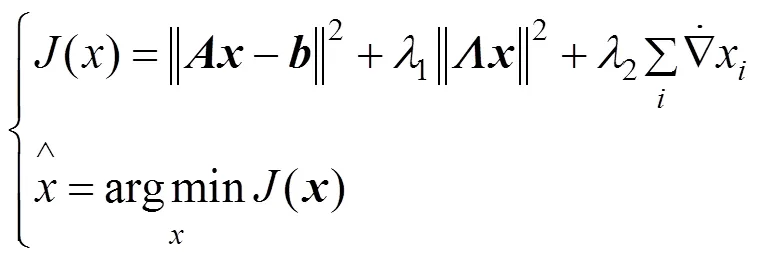
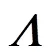
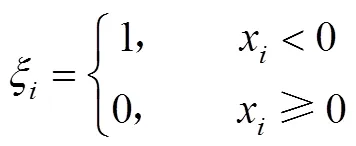
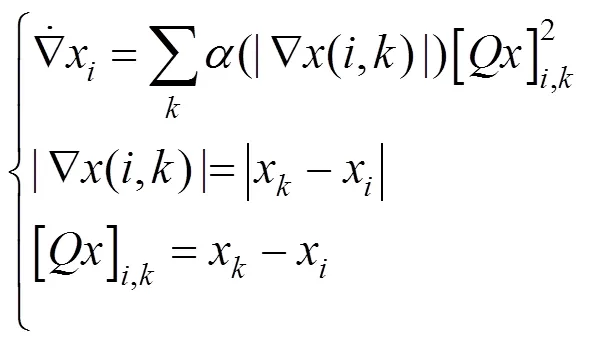
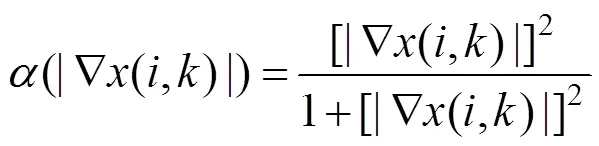
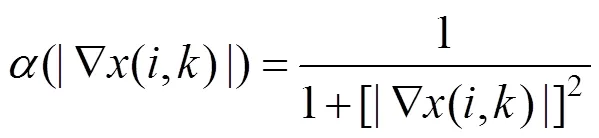
采用基于松弛滞后迭代极小化方法来求解式(6)，即

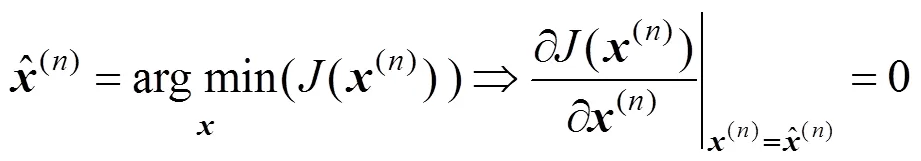
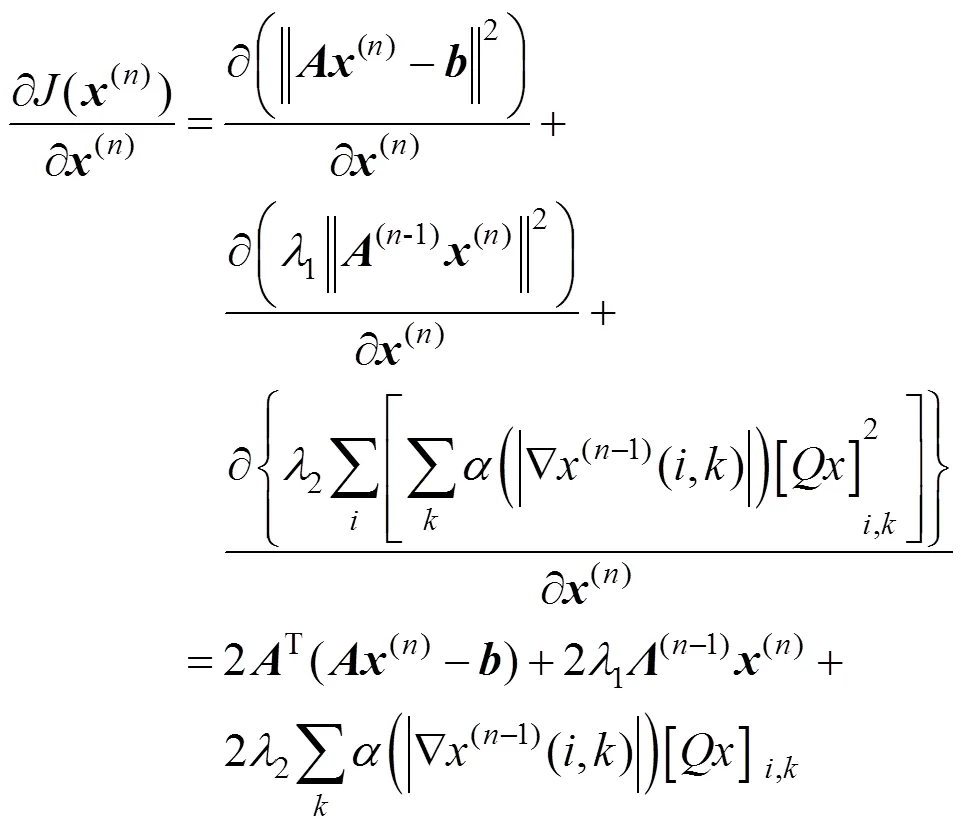
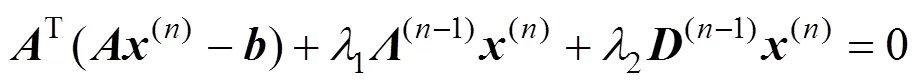
根据式(12)可得到的迭代求解关系为

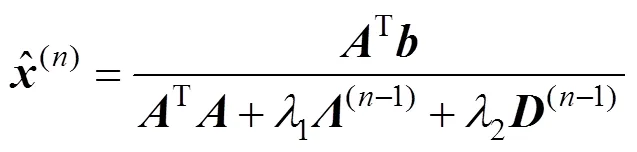
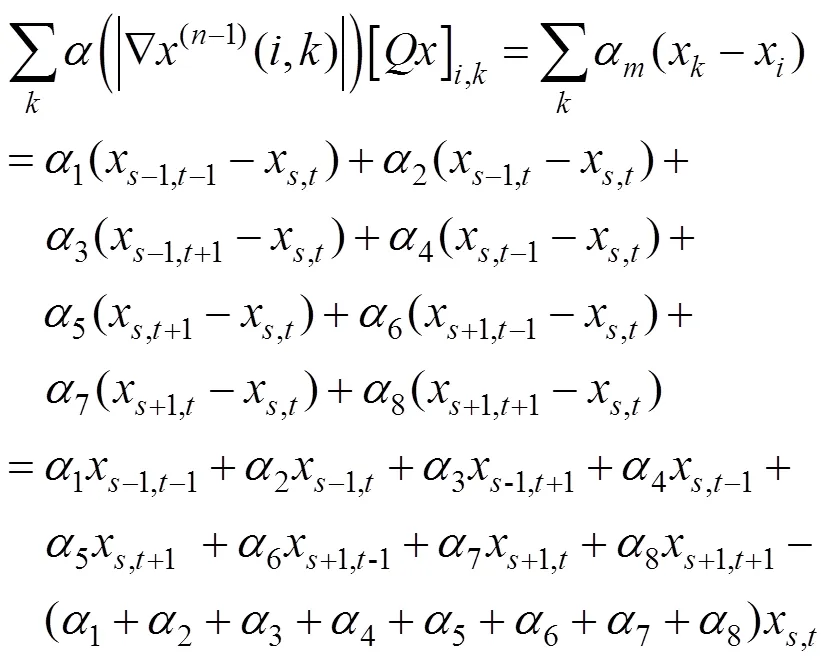
2.4 复原图像

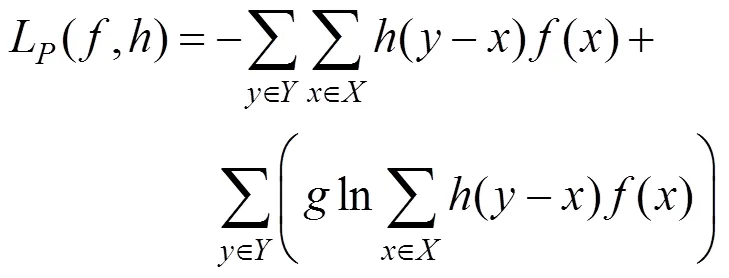
为了避免出现各向同性正则化得到过光滑的图像边缘现象，使用各向异性正则化方法，对大梯度使用小平滑系数，而对小梯度使用大的平滑系数。其代价函数如式(16)

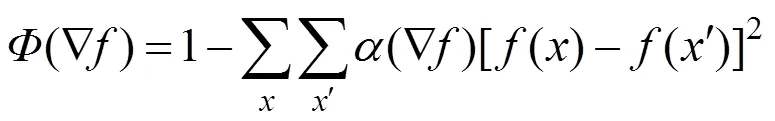
将其加入对数似然函数式(15)中，即可得到带有保边缘正则化项的似然函数，即

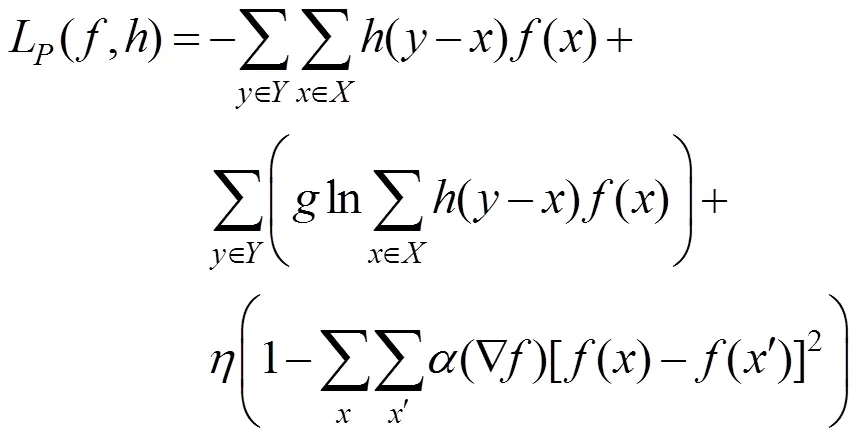
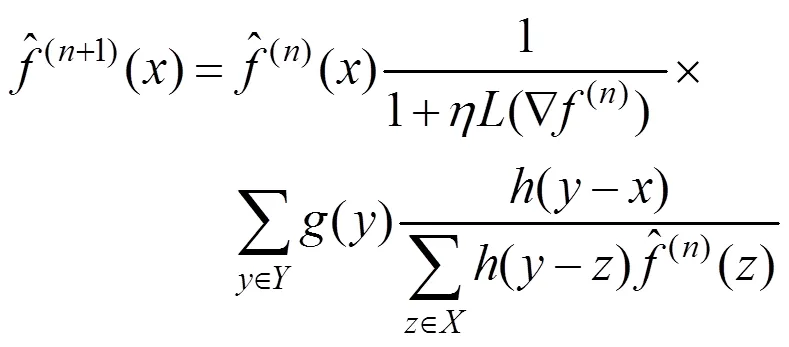
3 实验与分析

为了验证本文提出的图像去模糊高清晰化算法的有效性，在Intel M460 I5双核处理器、主频为2.53 GHz，内存为4 GB的硬件环境进行测试，编程软件为VC++6.0。

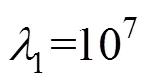
图5 同退化模式的仿真图像

图6 实际点扩散函数(PSF)

图7 本文方法求解得到的点扩散函数(PSF)

实验2.仿真图像复原实验及分析。图8~10分别是运动模糊仿真图像的复原、散焦模糊仿真图像的复原和气动模糊仿真图像的复原。从图8~10可发现NAS-RIF复原方法对散焦模糊退化图像复原有效果，对运动模糊和气动模糊退化图像恢复效果较差，没有复原出真实的图像；TV复原方法虽然有复原效果，但不够清晰；本文复原方法不论对那种模糊退化图像都能够较好地复原，且复原出的图像轮廓比较清晰。这主要原因是本文的点扩散函数求解是通过主要轮廓的边缘区域信息获得的，避免了图像平坦区冗余的信息对点扩散函数的求解带来不利的影响。同时在目标函数中融入了非负性约束和空间相关性约束，并在迭代过程中采用各项异性正则化方法保留图像的边缘，对大梯度使用小平滑系数，对小梯度使用大的平滑系数，使得恢复出来的图像较清晰。

图8 运动模糊仿真图像的复原比较

图9 散焦模糊仿真图像的复原比较

图10 气动模糊仿真图像的复原比较

表1列出了本文算法和TV算法对图8~10中的模糊图像估算的点扩散函数归一化均方误差，从表中可发现本文算法估算的点扩散函数归一化均方误差较小。表2列出了3种算法分别对图8~10中模糊图像复原的PSNR值，通过比较可以发现本文的PSNR值最大，进一步说明了本文算法优越性。

实验3.实际图像复原实验及分析。为了验证本文算法对实际图像复原效果，本文进行了大量的测试，图11是其中的几幅图像，其中图11(a)从上到下依次是运动模糊，大气湍流和退化原因未知的模糊图像。从复原结果可以看出，图片上的字符，道路两旁的交通护栏、路灯、树木，钢板圆孔等都变得较清晰，从而证明了本文提出的复原算法具有一定的通用性，可以获得比较好的复原效果。

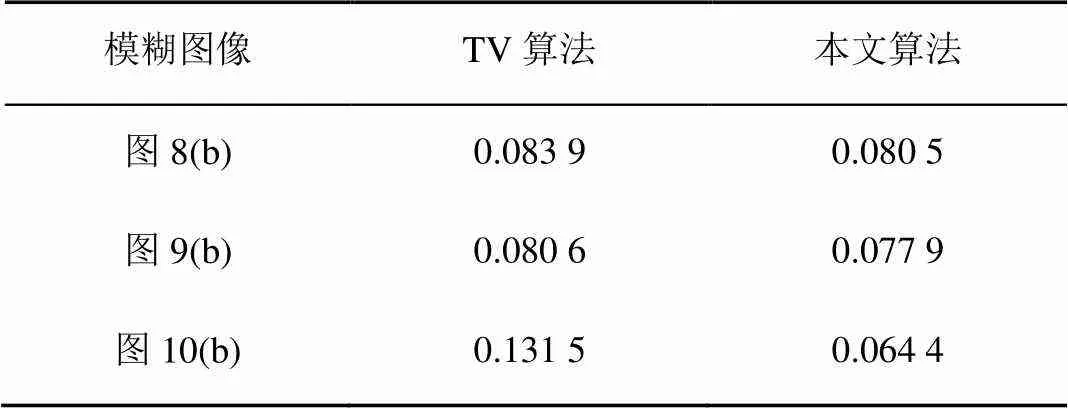
表1 PSF估算的归一化均方误差

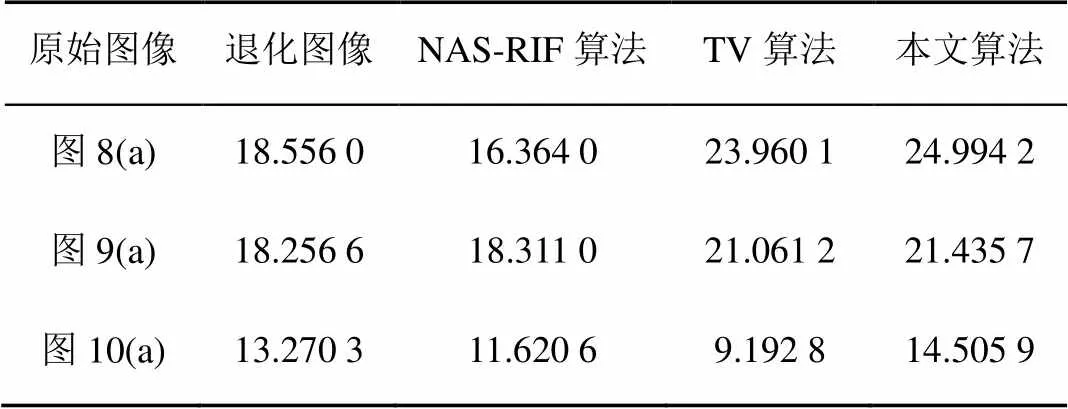
表2 不同复原结果的PSNR比较(dB)

图11 实际图像复原

4 结束语

针对目前的图像复原技术受到各种条件的限制，需要知道大量的先验知识，比如点扩散函数、退化模式、点扩散函数支持域大小等。本文在目前国内外图像复原技术的研究基础上，提出了一种在无需知道退化模式的情况下的实际图像去模糊清晰化方法。利用图像过渡区包含较多退化信息，建立关于点扩散函数的方程，同时，加入了非负惩罚项和空间相关性约束项以降低噪声的影响，并给出点扩散函数的迭代求解方程。最后对各种退化模式的图像进行了复原实验，并与现有的复原算法进行了比较。实验结果表明本文复原算法具有通用型，恢复效果较好。但是本文算法仍有很多之处值得研究和改进，即如何获得更加准确的模糊图像轮廓，在预测清晰图像过渡区时，如何更为有效的对细节进行控制，排除噪声的干扰等。

[1] 李旭超, 宋博. 改进的正则化模型在图像恢复中的应用[J]. 中国图象图形学报, 2014, 19(12): 1730-1742.

[2] 黄超, 刘传毅, 刘伟. 基于PSF参数估计与后处理的图像去模糊算法[J]. 计算机工程与设计, 2016, 37(9): 2485-2489.

[3] 杨东. 模糊降质图像恢复技术研究进展[J]. 计算机应用研究, 2016, 33(10): 2881-2888.

[4] SHI J P, XU L, JIA J Y. Discriminative blur detection features [C]//Proceedings of the Computer Vision and Pattern Recognition. New York: IEEE Press, 2014: 2965-2972.

[5] 陈春涛, 黄步根, 高万荣, 等. 最大熵图像复原及其新进展[J]. 光学技术, 2004, 30(1): 36-43.

[6] RICHARDSON W H. Bayesian-based iterative method of image restoration [J]. Journal of the Optical Society of America, 1972, 62(1): 55-59.

[7] 李勇, 范承玉, 时东封, 等. 基于加速正则化RL算法的大气湍流退化图像盲复原方法[J]. 大气与环境光学学报, 2011, 6(5): 342-350.

[8] YUAN L, SUN J, LONG Q, et al. Image deblurring with blurred/noisy image pairs [J]. ACM Transactions on Graphics, 2007, 26(3): 1-10.

[9] 吴晓旭, 刘秀平, 刘宇, 等. 局部加权全变差下的盲去模糊[J]. 计算机辅助设计与图形学学报, 2014, 26(12): 2173-2181.

[10] AYERS G R, DAINTY J C. Iterative blind deconvolution method and its applications [J]. Optics Letters, 1988, 13(7): 547-549.

[11] HE C, HU C H, ZHANG W, et al. Box-constrained total-variation image restoration with automatic parameter estimation [J]. Acta Automatica Sinica, 2014, 40(8): 1804-1811.

[12] 任福全, 邱天爽. 基于二阶广义全变差正则项的模糊图像恢复算法[J]. 自动化学报, 2015, 41(6): 1166-1172.

[13] KUNDUR D, HATZINAKOS D. A novel blind deconvolution scheme for image restoration using recursive filtering [J]. IEEE Transactions on Image Process, 1998, 46(2): 375-390.

[14] FERGUS R, SINGH B, HERTZMANN A, et al. Removing camera shake from a single photograph [J]. ACM Transactions on Graphics, 2006, 25(25): 787-794.

[15] HONG H Y, LI L C, ZHANG T X, et al. Universal deblurring method for real images using transition region [J]. Optical Engineering, 2012, 51(4): 1-9.

A New Method for Image Deblurring and Clearness

WANG Wenhao, YAN Yunyang, JIANG Mingxin, YU Yongtao, ZHAO Wendong

(Faculty of Computer & Software Engineering, Huaiyin Institute of Technology, Huaian Jiangsu 223003, China)

Due to the various limitations in real restoration process, it is difficult to get the image blur mode or point spread function (PSF). A new method for image deblurring is proposed in this paper. At first, the proposed deblurring method uses the different of Gaussian operator (DoG) to detect the counters of blur image. Then the information of transition region of original image can be predicted according to the contours of blur image. Then the objective function is established according to the original image, transition region, and point spread function. In order to overcome the influence of noise, the nonnegative penalty term and space correlation penalty term with anisotropic features are added in objective function, and the PSF is solved using the minimization method of hysteresis iteration. Finally, the clear image can be gained by the existing the non-blind image restoration methods. Experimental results show that the proposed method can effectively restore the blur images caused by various factors. It does not need to know the image blur model.

image deblurring; clearness; transition region; point spread function

TP 391

10.11996/JG.j.2095-302X.2018020193

A

2095-302X(2018)02-0193-08

2017-06-20；

2017-07-18

国家自然科学基金项目(61403060，61603146)；江苏省六大人才高峰项目(XYDXXJS-012)

王文豪(1973-)，男，江苏淮安人，副教授，硕士。主要研究方向为图形图像处理、模式识别。E-mail：wangwenhao1407@163.com