基于协方差矩阵修正的主瓣干扰抑制优化方法

，

(1.新疆财经大学计算机科学与工程学院，新疆 乌鲁木齐 830012；2.装甲兵工程学院，北京 100072)

0 引言

拖线阵声纳在探测水下未知目标时，水下常会存在大量并非我们所想探测的“假目标干扰”，如果不能对其进行有效抑制或滤除，空间存在的其他“弱真目标”将不能被有效检测，更不能为后续参数估计提供有效信息[1]。针对干扰下的“弱真目标”检测和方位估计问题，目前主要方法为阵元域预处理法，当存在强干扰时，首先采用阵元域预处理法将其滤除，然后再通过波束形成将“弱真目标”在波束图中显示出来。现有阵元域预处理方法主要有干扰阻塞法[2-5]、零陷波束形成法[6]、逆波束形成法[7]、空域滤波法[8-9]、子空间法[10-15]等方法。

由于干扰阻塞算法(Jamming Jam Method，JJM)简单方便，常被作为主瓣干扰抑制方法应用于工程实践中，但该方法在采用阻塞矩阵(Blocking Matrix，BM)对拖线阵接收信号进行阻塞预处理时，虽然不会改变“弱真目标”辐射信号波达方向，但会导致其辐射信号复包络发生改变，致使阻塞预处理后的协方差矩阵失配，存在干扰抑制后主波束指向偏移、波束变形以及探测盲区等问题。本文针对基于阻塞矩阵实现主瓣干扰抑制而导致的波束畸变和探测盲区问题，提出了基于协方差矩阵修正的主瓣干扰抑制优化方法，从本质上改善了阻塞预处理后的协方差矩阵失配问题，减小了干扰抑制后主波束指向偏移、波束变形以及探测盲区。

1 基于阻塞矩阵预处理的主瓣干扰抑制方法

1.1 理论分析

以频域数据处理为例，对于间距为d的N元等间隔水平拖线阵，有一个强干扰从θ0入射，有P个目标从θp入射，在第n阵元接收数据中，角频率wl对应数据Xn(wl)可表示为：

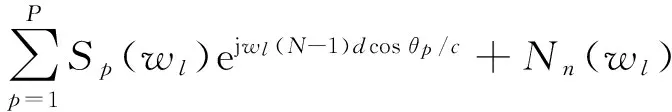
(1)

式(1)中，S0(wl)为强干扰频域表示形式，Sp(wl)为第p目标辐射信号的频域表示形式，Nn(wl)为第n阵元接收加性高斯白噪声数据的频域表示形式，c为声速。

则拖线阵各阵元接收数据的向量形式为：

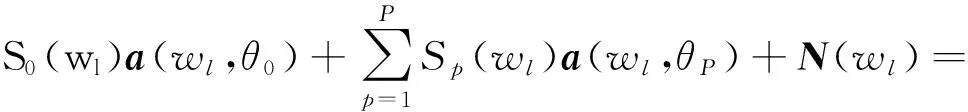
(2)

式(2)中，a(wl,θ0)=[1,ejwldcosθ0/c,…,ejwl(N-1)dcosθ0/c]T为强干扰对应N×1维阵列流形矢量，a(wl,θP)=1,ejwldcosθp/c,…,ejwl(N-1)dcosθp/cT为第p个目标辐射信号对应N×1维阵列流形矢量，A=[a(wl,θ0),a(wl,θ1),…,a(wl,θP)]为N×(P+1)维阵列流形矩阵，S(wl)=[S0(wl),S1(wl),…,SP(wl)]为(P+1)×1维频域数据向量，[·]T为矩阵转置。N(wl)=N1(wl),N2(wl),…,NN(wl)T为背景噪声频域向量。

基于阻塞矩阵预处理的主瓣干扰抑制方法(干扰阻塞算法)是利用强干扰入射角θ0构造阻塞矩阵，对各阵元接收数据X(wl)进行主瓣干扰相消预处理，将干扰阻塞掉。阻塞矩阵构造如下所示：

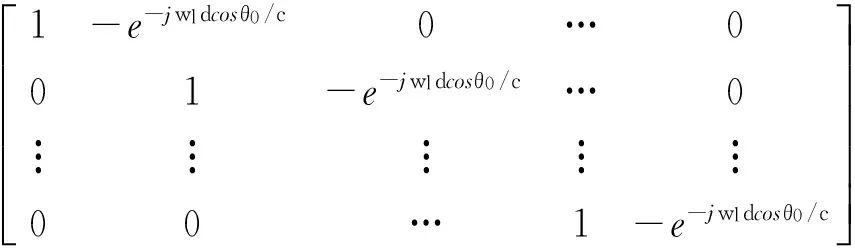
(3)

利用阻塞矩阵对各阵元接收数据X(wl)进行阻塞处理，可得：

WX(wl)=WAS(wl)+WN(wl)=
A′S(wl)+WN(wl)=
A″S′(wl)+WN(wl)

(4)

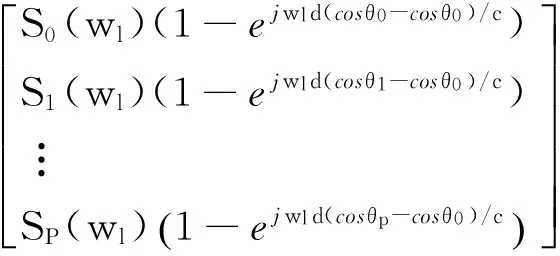
由S′(wl)可知，阻塞矩阵可以阻塞掉强干扰。但在阻塞强干扰时，目标辐射信号也受到了影响。阻塞矩阵阻塞强干扰后，拖线阵接收信号为：

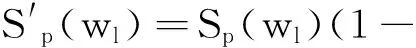
(5)

由1-ejwld(cosθp-cosθ0)/c可知，在阵间距d、目标辐射频率wl、干扰方位角θ0一定时，当目标位于空间某些方位区间，即1-ejwld(cosθp-cosθ0)/c<1时，目标辐射信号的复包络被减弱，当目标位于空间某些方位区间时，即1-ejwld(cosθp-cosθ0)/c>1时，目标辐射信号的复包络被增强，该变化将对波束形成结果造成不同程度影响，导致预处理后的波束形成发生畸变，在某些方位区间形成探测盲区，影响最终探测效果。

1.2 仿真分析

为了详细说明，在不同方位区间，阻塞矩阵预处理会对拖线阵接收目标辐射信号造成不同程度增减。接下来依据阻塞矩阵预处理后的目标辐射信号复包络变化量(1-ejwld(cosθp-cosθ0)/c)，进行如下数值仿真分析。

1)目标辐射信号频率为fl=60 Hz，则角频率wl=2πfl，声速为c=1 500 m/s，波长为λ=c/fl，阵元间距d=λ/2。图 1为不同强干扰方位角θ0情况下，阻塞矩阵对拖线阵接收信号在不同方位下的仿真结果。

2)目标辐射信号频率为fl=60 Hz，则角频率wl=2πfl，声速为c=1 500 m/s，波长为λ=c/fl，强干扰方位角为θ0=30°。图 2为一定强干扰方位角和不同阵元间距d情况下，阻塞矩阵对拖线阵接收数据在不同方位下的仿真结果。

由图1和图2可知，由于阻塞矩阵预处理改变了目标辐射信号的复包络，在信号频率一定时，影响衰减区间相关因子主要为阵元间距d、强干扰方位角θ0。在阵间距d、干扰方位角θ0设定后，阻塞矩阵预处理对拖线阵接收信号影响最大的因素为目标相对拖线阵方位，阻塞矩阵预处理会增大位于空间某些方位区间目标信号复包络幅度，同样也会减小位于空间另外一些方位区间目标信号复包络幅度，数值仿真结果与理论分析相一致。

2 基于协方差矩阵修正的主瓣干扰抑制优化方法

由式(4)知，经过阻塞矩阵预处理，会损失一个阵元的自由度，即预处理后信号阵列流形矢量相对于未预处理的阵列流形矢量少了一维，同时经阻塞矩阵预处理后的协方差矩阵为

R′(wl)=EWX(wl)(WX(wl))H=
EW(AS(wl)+N(wl))(WAS(wl)+WN(wl))H=
W·E(AS(wl)+N(wl))(AS(wl)+N(wl))H·WH=
WR(wl)WH

(6)

令各阵元接收信号与背景噪声、背景噪声与背景噪声之间互不相关。由式(6)可知，阻塞矩阵预处理后协方差矩阵可具体表示为：

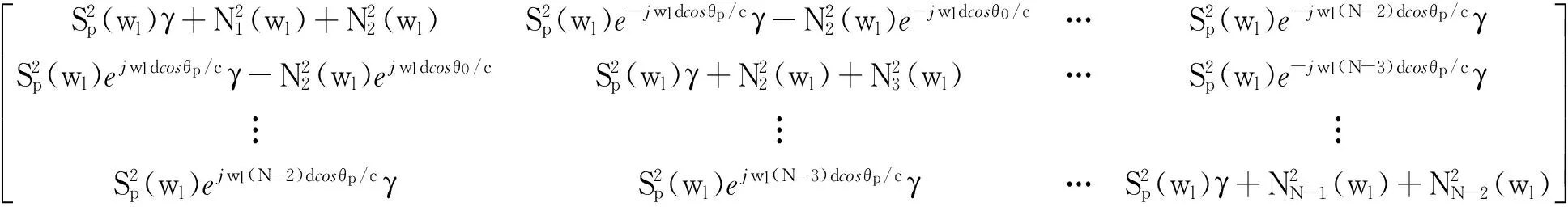
(7)

式(7)中，γ=(2-ejwld(cosθp-cosθ0)/c-ejwld(cosθp-cosθ0)/c)。

对式(6)所示协方差矩阵进行常规波束形成，可得到经阻塞矩阵预处理后的空间谱为：

(8)

由于阻塞矩阵预处理前后协方差矩阵在信号和噪声项都具有一定差别，而阻塞矩阵预处理前后波束形成过程中所用导向向量一致，因此，除在干扰方位之外，阻塞矩阵预处理前后波束形成在其他方位的处理结果存在一定差别。相比于利用理想协方差矩阵，JJM在波束形成过程中存在协方差矩阵失配，或称为误差，因而也就出现了波束畸变和探测盲区问题。

由上节理论分析和式(6)所示可知，阻塞矩阵预处理前后拖线阵接收信号变化了(1-ejwld(cosθ-cosθ0)/c)，在信号频率一定时，影响拖线阵接收信号变化相关因子主要为阵元间距d、强干扰方位角θ0。针对该情况，本文采用修正因子WWH+αI对阻塞矩阵预处理后的协方差进行修正，以实现JJM进行优化，优化公式如下：

(9)

(10)

由式(10)可知，WWH+αI为埃尔米特矩阵(自共轭矩阵)，式中增加角加载为了根据实际需要调节干扰抑制后衰减区间补偿量，α越接近0，补偿后的衰减区间越小，本文在数值仿真分析和实测数据处理分析中均将α置为0，以便得到最小衰减区间。

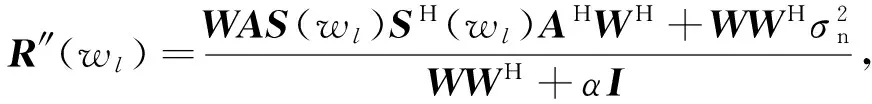
3 验证分析

3.1 数值仿真分析

为了进一步验证本文方法可以有效优化干扰阻塞算法，实现波束校正，减小探测盲区，实现原衰减区间内目标的有效检测，提高干扰阻塞算法抗干扰性能和检测性能，接下来进行如下仿真分析。

仿真条件如下：强干扰、弱目标1与弱目标2信号频率均为fs=80 Hz，强干扰、弱目标1与弱目标2方位角分别为θ0=30°、θ1=33°和θ2=160°，背景噪声为带宽fn=60～100 Hz的高斯白噪声，声速为c=1 500m/s，阵元间距为d=λ/2，λ=c/fs，阵元数为fn=64。弱目标1与弱目标2谱级比为0 dB，弱目标1与强干扰谱级比为-25 dB，弱真目标1与背景噪声信噪比为-30 dB。图 3至图 6由不同方法在fs频率单元处所得。

由图3至图6可知，在抑制θ0=30°方位处强干扰时，由于JJM中阻塞矩阵预处理会造成拖线阵接收信号协方差矩阵失配，对波束形成结果造成不同程度影响，导致阻塞矩阵预处理后的波束形成发生畸变，致使干扰抑制后波束形成在0～180°内输出能量呈现如图 4和图 6中JJM所示的“凸”字形，对应中间方位区域输出能量较大，两侧方位区域输出能量较小，在两侧方位区间形成探测盲区(如图 1中θ0=30°对应曲线，输出信号能量在100°最大，然后向两侧衰减)，影响最终探测效果，导致θ1=33°和θ2=160°处弱目标不能被协方差矩阵失配后的波束形成实现有效检测；而本文方法对阻塞矩阵预处理协方差矩阵进行了修正，优化JJM，降低了阻塞矩阵预处理对拖线阵接收信号协方差矩阵造成的影响，在抑制θ0=30°处强干扰时，θ1=33°和θ2=160°处弱目标被有效检测出。数值仿真结果验证了，本文方法通过对阻塞矩阵预处理后协方差矩阵进行修正，优化了干扰阻塞算法，实现了波束校正，减小了探测盲区，对强干扰相邻3°的弱目标实现了有效检测。

3.2 实测数据处理分析

本次试验中采用40元水平拖线阵拾取水中数据，相邻阵元间隔为Xm，水平线阵首端方向设为0°。

本次处理数据长度为300 s，所用采样率为fs=5 kHz。滤波器频带为f=60～120 Hz，图 7至图 10由不同方法所得结果。

由图7至图10可知，在抑制θ0=71°附近强干扰时，由于JJM中阻塞矩阵预处理会造成拖线阵接收信号协方差矩阵失配，导致阻塞矩阵预处理后的波束形成发生畸变，致使干扰抑制后波束形成在0～180°内输出能量呈现如图 8和图 10中JJM所示的“宽凹”字形，对应中间71°方位区域输出能量最小，两侧方位区域输出能量较大，在中间71°方位区间形成较宽的探测盲区(如图 1中θ0=60°对应曲线)，影响最终探测效果，协方差矩阵失配后的波束形成不能对强干扰相邻的弱目标实现有效检测；而本文方法对阻塞矩阵预处理协方差矩阵进行了修正，优化JJM，降低了阻塞矩阵预处理对拖线阵接收信号协方差矩阵造成的影响，在抑制θ0=71°附近强干扰时，强干扰相邻弱目标被较好地检测到，即两个交叉运动目标在强干扰被抑制时能够被较好地检测到。试验数据处理结果同样验证了，本文方法通过对阻塞矩阵预处理后协方差矩阵进行修正，优化了干扰阻塞算法，实现了波束校正，减小了探测盲区，对强干扰相邻3°的弱目标实现了有效检测。

4 结论

本文提出了基于协方差矩阵修正的主瓣干扰抑制优化方法。该方法首先通过阻塞矩阵构造协方差修正因子；然后利用修正因子对阻塞矩阵预处理后协方差进行修正，减小协方差矩阵失配引起的波束畸变和探测盲区；最后采用修正后的协方差实现对干扰阻塞算法优化，达到预期的干扰抑制效果和检测效果。

数值仿真和数据处理验证表明，本文方法通过对阻塞矩阵预处理后协方差矩阵进行修正，优化了基于阻塞矩阵预处理的主瓣干扰抑制方法(干扰阻塞算法)，能够对强干扰相邻3°的弱目标实现有效检测，有效降低了干扰阻塞算法形成的“宽凹”或“凸”字形波束对不同方位区间目标检测结果的影响，实现了波束校正，减小了探测盲区，提高了干扰阻塞算法抗干扰性能和检测性能。

参考文献:

[1]高阳,许稼,贾鑫,等.自适应阵列抗干扰性能的解析定量分析[J]. 电波科学学报, 2015, 30 (4)： 729-735.

[2]李荣峰,王永良,万山虎.主瓣干扰下自适应方向图保形方法的研究[J]. 现代雷达, 2002, 24 (3)： 50-53.

[3]苏保伟,王永良,李荣峰,等.阻塞矩阵方法对消主瓣干扰[J]. 系统工程与电子技术, 2005, 27(11) ： 1830-1832.

[4]刘聪锋,杨洁,甘昶.加载与约束结合的主瓣干扰抑制方向图保形[J]. 电波科学学报, 2012, 27(2)： 344-349.

[5]高阳,许稼,龙腾.阻塞矩阵抗干扰方法性能分析[J]. 信号处理, 2015, 31(10)： 1361-1365.

[6]李文兴,毛晓军,孙亚秀.一种新的波束形成零陷展宽算法[J]. 电子与信息学报,2014,36(12)： 2882-2888.

[7]葛士斌,陈新华,孙长瑜.具有良好宽容性的逆波束形成干扰抑制算法研究[J]. 电子与信息学报, 2015, 37(2)： 380-385.

[8]韩东,张海勇,黄海宁,等.基于远近场声传播特性的拖线列阵声纳平台辐射噪声空域矩阵滤波技术[J].电子学报,2014,42(3)：432-438.

[9]韩东,李建,康春玉,等.拖曳线列阵声呐平台噪声的空域矩阵滤波抑制技术[J]. 声学学报, 2014, 39(1)： 27-34.

[10]方庆园,韩勇,金铭,等.基于噪声子空间特征值重构的 DOA 估计算法[J].电子与信息学报, 2014, 36(12)： 2876-2881.

[11]OLFAT Ali, NADER-ESFAHARI Said. A new signal subspace processing for DOA estimation[J]. Signal Processing, 2004, 84(4)： 721-728.

[12]RANGARAO Kaluri V, VENKATANA- RASIMHAN Shridhar. a variation on MUSIC to accurately determine peaks of the spectrum[J]. IEEE TRANS ANTENNA & PROPAGATION, 2013, 61(4)： 2263-2268.

[13]GU Yujie, LESHEM Amir. Robust adaptive beamforming based on interference covariance matrix reconstruction and steering vector estimation[J]. IEEE Transactions on Signal Processing, 2012, 60(7)： 3881-3885.

[14]HARRISON Brian F. The eigencomponent association method for adaptive interference suppression[J]. Journal of the Acoustical Society of America.2004, 115(5)： 2122-2128.

[15]郭鑫,葛凤翔,任岁玲, 等. 一种最差情况下性能最优化的特征分析自适应波束形成方法[J]. 声学学报, 2015, 40(2)： 187-197.