基于FRFT的雷达辐射源信号特征分析及提取

，，

(海军航空工程学院，山东 烟台 264001)

0 引言

随着现代雷达技术的快速发展，各式新体制的雷达应用不同的战场空间，同一时间同一地点的辐射源信号密集交错，调制形式灵活多样，由基本参数所描述的特征空间边界严重交错，这使得基于传统基本参数分选的性能大大下降。一种有效减少特征空间交错的方法就是引入新的雷达辐射源信号分选的特征向量。

近些年来，诸如模糊函数[1]，双谱特征[2-3]以及时频原子分解[4-6]的方法都广泛应用于雷达辐射源信号特征向量的提取中。鉴于分数阶傅里叶变换较传统傅里叶变化具有更好的时频分布特性，为解决特征空间交错的问题，本文基于FRFT的理论，提出新的雷达辐射源信号特征定义，通过分析计算不同阶FRFT中的聚散度和相像系数得到相应的变化曲线，提取曲线峰值对应的阶数值和峰度，并进一步提取信号做k次方谱的相像系数。

1 分数阶傅里叶变换

1.1 基本原理

分数阶傅里叶变换(FRFT)是近年来引起广泛关注的一种信号处理工具，作为传统傅里叶变换的广义形式，FRFT可以看作是信号在时域-频域平面上表示后坐标轴围绕原点逆时针旋转任意角度后形成的表示方法。

FRFT的基本定义为：定义在t域上的函数x(t)的p阶分数阶傅里叶变换是一个线性积分运算，即

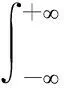
(1)

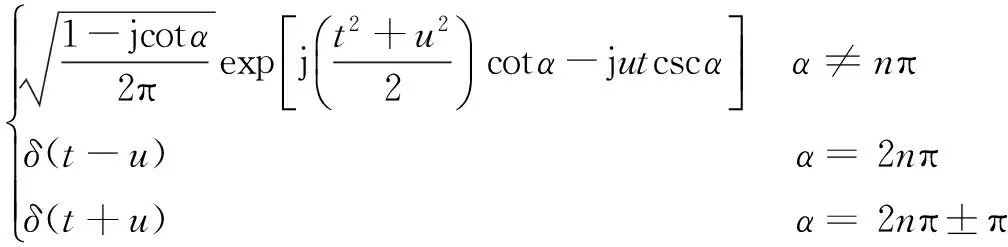
(2)

FRFT与传统傅里叶变换有着相当紧密的联系，同时又具有传统傅里叶变换不具备的优势，对信号的处理更灵活。传统傅里叶变换即是时频平面旋转π/2后的表示，得到的仅仅是信号整体的频谱特征，没有对信号频率随时间的变化进行细致描绘，因此仅适用于处理平稳的随机信号；而信号在FRFT域上表示，同时包含了信号的时域信息和频域信息，应用范围更广，前景更好。

1.2 快速计算

关于FRFT的计算方法，最经典的当属Ozaktas提出的分解型算法[9]，该算法的基本思想是把连续复杂的FRFT积分变换逐步分解成几个简单的计算过程，然后再通过离散化达到离散的卷积表达式，最后通过FFT计算最终的FRFT。

α≠nπ时，FRFT定义式可以改写为如下形式：

(3)

FRFT可分解为如下四个步骤，如图1所示。

其中，每个分解计算步骤都需要进行相应的离散化操作，最终通过FFT计算即可得到FRFT变换的结果。

2 信号特征分析及提取方法

以CW、LFM、QPSK信号为例，分别画出其阶数为0.6，0.8，1，1.2，1.4时的FRFT图，如图2所示。

从图2中可以看出，同一信号的不同阶FRFT是不同的，直观体现在其聚散程度上，因此，本文通过自定义的信号聚散度来描绘这种特征，同时利用相像系数来表征体现不同信号频谱的差异程度。

2.1 参数定义

定义一：信号聚散度

从统计学中对偏度以及峰度的定义得到启发，本文定义新的特征量——信号聚散度如下：

(4)

式中，Pvc(i)为雷达辐射源信号归一化的幅值，其具体定义为：

(5)

式中，P(i)为实际幅值。

以上述的CW，QPSK信号为例，阶数不同时其聚散度(数据均归一化)如表1所示。

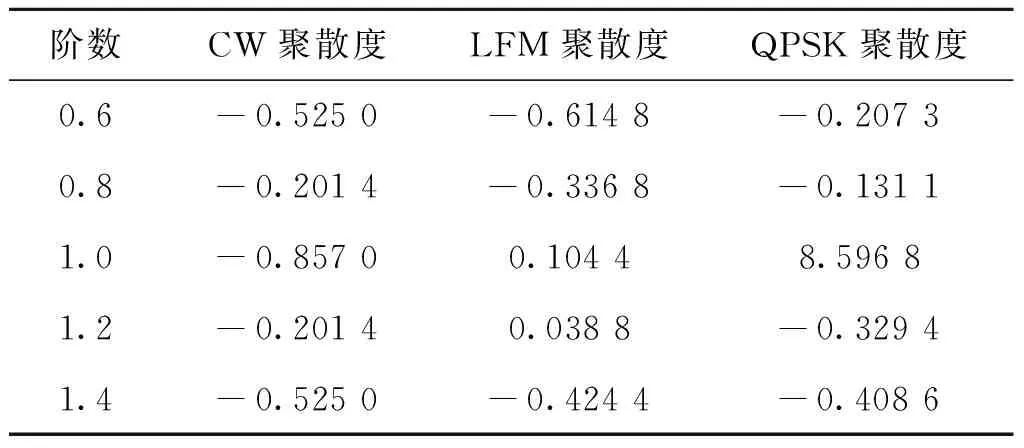
表1 不同信号的聚散度Tab.1 Different signals’ vergence

从图3中可以看出，三种不同的信号的聚散度随着FRFT的阶数变化其变化的趋势程度上是有所不同的，因此可以将基于同一信号的聚散度随着FRFT的阶数变化的特征可以作为一个稳定的特征向量。

定义二：信号k次方谱的相像系数

信号的k次方谱即信号k次方后的频谱，k次方谱可以进一步反映调制信号在频谱上的细微分布特性。

相像系数是对不同信号之间相似程度的一种度量，定义如下：

两个一维离散序列S1(i)和S2(i),定义系数：

(6)

为序列S1(i)和S2(i)的相像系数。

雷达辐射源信号脉冲序列包含许多脉冲，若逐一计算所有脉冲频谱相互之间的相像系数，计算量非常大，因此应该选取几个自身特征明显的信号作为参照信号，分别计算脉冲序列和它们之间的相像系数，这样可以大大减少计算量。

本文仅选取了矩形信号作为参照信号。

矩形信号：

(7)

所谓信号k次方谱的相像系数即对信号k次方谱在不同阶FRFT下，与矩形信号计算相像系数，反映其与矩形信号的相像程度。

2.2 参数分析过程

步骤1：提取雷达辐射源信号脉冲序列的脉冲，进行相应的预处理，包括带宽和能量的归一化；

步骤2：对接收的信号进行不同阶数的傅里叶变换；

步骤3：计算信号在不同阶傅里叶变换下的聚散度；

步骤4：比较确定聚散度的最终提取参数；

步骤5：计算信号不同阶分数阶傅里叶变换下的1次相像系数；

步骤6：进一步计算信号不同阶分数阶傅里叶变换下的k次相像系数；

步骤7：比较确定相像系数的最终提取参数；

步骤8：综合确定最终提取的参数及参数提取步骤。

具体流程图如图4所示。

3 仿真验证分析

3.1 仿真条件

硬件：计算机，内存4G。

软件：Windows操作系统Matlab2016。

3.2 仿真实验

为全面体现雷达辐射源信号的脉内特征情况，本文选取以下七种常见的典型雷达辐射源信号作为分析对象进行仿真分析：

1)连续波信号(CW)；

2)线性调频信号(LFM)和非线性调频信号(NLFM)；

3)频率编码信号(FSK)，采用巴克编码方式；

4)相位编码信号，包括二相编码信号(BPSK)，四相编码信号(QPSK)以及八相编码信号(8PSK)，均采用弗兰克编码方式。

文献[12]中通过FRFT搜索得到包络曲线函数，提取该函数峰值对应的阶数值、峰值大小以及包络曲线的峰度作为雷达辐射源信号新的特征向量。

基于上述七种典型雷达辐射源信号，本文对文献[12]中的特征提取方法进行仿真实验，得到结果如图4所示。

从图5中可以看出，不同类型的信号α域包络曲线出现峰值的FRFT的阶数是有所差别的，但图中也表明，这种差别并不是很大，例如，不同类型的相位编码信号，峰值基本都出现在阶数等于1上，尽管峰值的大小不一样，但峰值的大小与辐射源信号的脉宽有一定的联系，因此峰值的大小并不能作为一个稳定准确的分选特征向量。

按照文献[12]特征提取自动分类，提取峰值对应阶数可以轻易分选出LFM、NLFM，同时再对峰度进行计算提取，即可以对BPSK以及FSK信号进行分类，但根据图6中显示，CW、QPSK和8PSK信号曲线几乎完全重合，无法根据峰度以及峰值对应分数阶数将之分离。

现对本文信号聚散度和相像系数仿真分析。

1)聚散度

对七种不同信号进行不同阶FRFT的变换，计算其在每一个分数阶中的聚散度，这些聚散度随着分数阶次的变换得到曲线如图7所示。

观察图7，不同信号聚散度曲线的尖峰出现在不同位置，其中LFM和NLFM信号峰值出现在分数阶数p=1.04和p=1.08处而不是在p=1.0处，而CW信号在p=1.0却出现与其他信号完全相反的情况——出现谷值，因此从图中可以清楚地分离CW、LFM、NLFM信号，去除上述三个信号得到图8。

观察图8，四种信号的峰值虽然都出现在分数阶数p=1.0处，然而其变化趋势却是截然不同的，图中可以看出FSK信号和BPSK信号的曲线是近似关于p=1.0对称的，而QPSK和8PSK信号则不然；同时，尽管QPSK和8PSK信号的变化趋势基本相同，但从p<1和p>1的变换趋势中可以看出，p<1时8PSK信号曲线上升变化比QPSK明显，而p>1时，QPSK信号曲线下降变化比8PSK明显。

因此利用文献[12]中对曲线峰度的提取方法对聚散度变化曲线进行峰度的提取，可以对四种信号进行区分。

2)相像系数

对七种不同信号进行不同阶FRFT变换，计算其在每一个分数阶域中与矩形信号的相像系数，这些相像系数随着分数阶变换得到曲线如图8所示。

根据相像系数的定义，相像系数的模值不会随信号幅度的变换而发生巨大的变化，根据信号的不同，相像系数的模值作为特征向量是相对比较稳定的。

观察图9，不同信号相像系数曲线的尖峰出现在不同位置，其中LFM和NLFM信号峰值出现在分数阶数p=1.04和p=1.08处而不是在p=1.0处，而FSK信号的变化趋势与其他信号完全相反，同时CW信号p=1.0处的幅值明显异于相位编码信号，因此从图中可以清楚地分离CW、FSK、LFM、NLFM信号，去除上述四个信号得到图10。

从图10中可以看出，三种相位编码信号相像系数随分数阶变换的趋势大致相同，但在p=0.5和p=1.5处可以看出BPSK信号和另外两种信号模值上的差异。

据此，基于p=0.5的FRFT，本文再对信号的k次方谱下的相像系数继续仿真实验，对三种信号进一步分析，细化差异。

对三种相位编码信号进行0.5～8次方处理，同时进行p=0.5阶的FRFT的变换，分别计算其与矩形信号的相像系数，这些相像系数随着信号k次方的变换得到曲线如图11所示。

从图11中可以看出，三种相位编码信号通过信号4，4.5和5次方处理后，通过相像系数模值可以进行有效的区分，其中以4.5次方的相像系数模值区分最优，实际情况中为了便于计算，选取信号5次方后FRFT的相像系数作为分选特征向量。

综上所述，结合两种基于FRFT的聚散度和相像系数，具体特征提取及自动分类步骤如下：

1)提取雷达辐射源信号脉冲序列的脉冲，进行相应的预处理，包括带宽和能量的归一化；

2)对接收到的信号进行阶数p∈[0.5,1.5]上分数阶傅里叶变换；

3)分别计算信号在不同阶傅里叶变换的聚散度和与矩形信号的相像系数；

4)提取不同信号聚散度变化曲线的峰度以及峰值对应的阶数；

5)提取不同信号相像系数变换曲线的峰值谷值及对应的阶数；

6)分选易分离信号后对剩余信号做信号5次方后的p=0.5阶的FRFT的变换，同时计算与矩形信号的相像系数；

7)根据信号5次方的相像系数进一步分选。

4 结论

本文基于FRFT的理论，提出新的雷达辐射源信号特征特征向量，通过计算不同阶FRFT中的聚散度和相像系数得到相应的变化曲线，提取曲线峰值对应的阶数值和峰度，并进一步提取信号做k次方谱的相像系数，一定程度上反映了信号自身以及信号之间的特征表征，更具有普适性，仿真分析对比的结果表明，本文提取的特征向量较已有的提取算法所提取的向量具有很好的可分性，可有效解决参数空间交叠的问题。

参考文献:

[1]普运伟等. 雷达辐射源信号模糊函数主脊切面特征提取方法[J]. 红外与毫米波学报, 2008,27(2)：133-137.

[2]陈昌孝，何明浩，朱元清，等.基于双谱分析的雷达辐射源个体特征提取[J].系统工程与电子技术,2008,30(6)：1046-1049.

[3]梁华东，韩江洪.采用双谱多类小波包特征的雷达信号聚类分选[J].光子学报，2014,43(3)：1-8.

[4]朱明, 金炜东, 胡来招,等. 基于原子分解的雷达辐射源信号二次特征提取[J]. 西南交通大学学报2007,42(6)： 659-664.

[5]王希勤，刘婧瑶，孟华东，等.一种基于时频原子特征的雷达辐射源信号识别方法[J]. 红外与毫米波学报,2011,30(6)：566-570.

[6]Mallat S，Zhang Z. Matching pursuit with time-frequency dictionaries[J]. IEEE Trans.on Signal Processing，1993,41(12)：3397-3415.

[7]韩俊，何明浩，朱振波，等.基于复杂度特征的未知雷达辐射源信号分选[J].电子与信息学报, 2009, 31(11)：2552-2556.

[8]何友,修建娟,张晶炜,等.雷达数据处理及应用(第二版)[M].北京：电子工业出版社,2009.

[9]陶然，邓兵，王越.分数阶Fourier变换及其应用[M].北京：清华大学出版社，2009.

[10]Alieva T, Bastiaans M J. On fractional fourier transform moments[J]. IEEE Signal Process. Lett,2000,7：320-323.

[11]Ozaktas H M, Arikan O, Kutay M A, et al. Digital computation of the fractional Fourier transform [J]. IEEE Trans on SP, 1996, 44(9)：2141-2150.

[12]司锡才，柴娟芳.基于FRFT的α域-包络曲线的雷达信号特征提取及自动分类[J].电子与信息学报, 2009,31(8)：1892-1897.