梁腹板偏心孔强度校核方法研究
王 震,王月英,张爱茹,张海周
(1.航空工业洪都,江西南昌330024;2.伊犁师范学院,新疆 伊宁835000)
0 引言
现代飞机结构强度校核工作中大量采用有限元软件计算载荷和应力,但在全机有限元模型简化中往往不可能将结构细节模拟出来。例如飞机翼梁有限元模型就常常用纯剪板元模拟梁腹板、用等轴力杆模拟梁缘条,并且认为梁腹板处没有开孔。然而,因安装、维护机载设备或管道通过(如通风管)的需要,梁腹板往往需要开孔。因此有限元结果只是近似解,腹板开孔部位需要用工程方法对有限元结果进行修正。目前有多种工程算法可以修正梁腹板上有口框的开孔区域的载荷。各种方法都是按腹板开孔的载荷传递路径假设来分配腹板总剪力,但在处理开孔偏心时,开孔处腹板剪力分配存在分歧,本文主要讨论两种处理方法:一是按开孔上、下部位剩余腹板高度比来分配,二是按梁缘条的剖面惯性矩的比值来分配。在具体工程实践中,多采用第二种方法进行机翼梁腹板开孔偏心情况的强度校核。具体方法如下(该计算过程取自某型飞机机翼翼梁强度校核报告)。
1 实例
1.1 实例1
如图1所示,已知梁腹板高度H=201mm,梁腹板厚度tw=2.5mm,腹板开孔长度L=75mm,梁腹板剪应力τ=-67.6MPa。
开孔上截面惯性矩I1=496405mm4,开孔下截面惯性矩I2=87035mm4
开孔上截面的附加弯矩为ΔM:
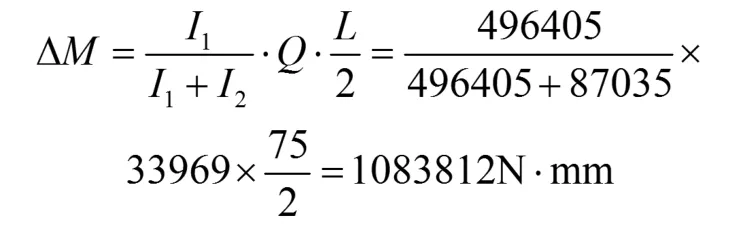
附加弯矩在上缘条产生的附加应力Δσ为:
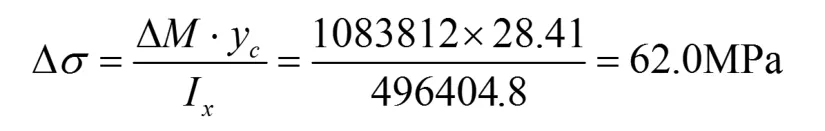
有限元结果,梁上缘条正应力为σ0=-298.4MPa梁上缘条正应力:σ=σ0+Δσ=298.4+62.0=360.4MPa已知梁缘条局部失稳临界应力σcr=365MPa则该段腹板开孔梁上缘条稳定性系数ξ为:
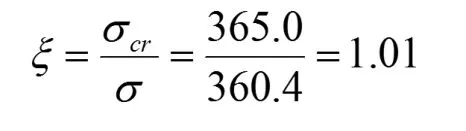
由以上校核过程可知,此处开孔刚刚满足静强度要求。
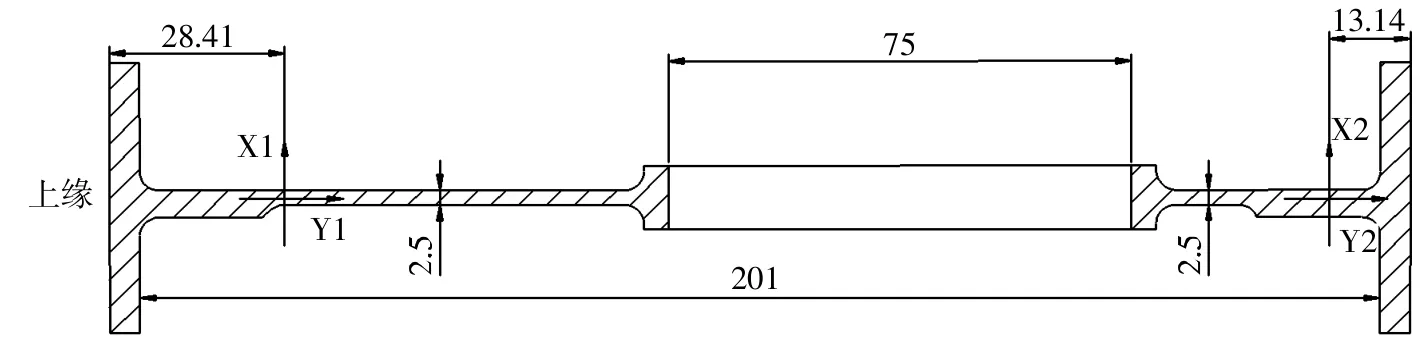
图1 梁腹板开孔截面
1.2 实例2
实例1中开孔向下偏心,距上缘条较远。假设开孔向上偏心,距上缘条较近,如图2所示。同样,按梁缘条的剖面惯性矩的比值来分配剪力。
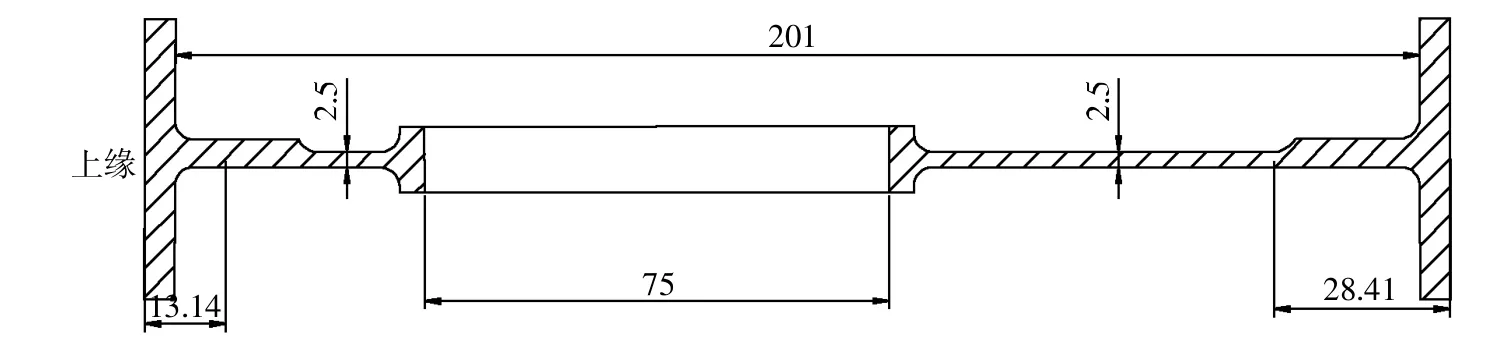
图2 梁腹板开孔截面
梁腹板处开孔参数及腹板应力与实例1相同。
剪力Q:Q=τ·tw·H=67.6×2.5×201=33969N
开孔上截面惯性矩I1=87035mm4,开孔下截面惯性矩I2=496405mm4
开孔上截面的附加弯矩ΔM为:
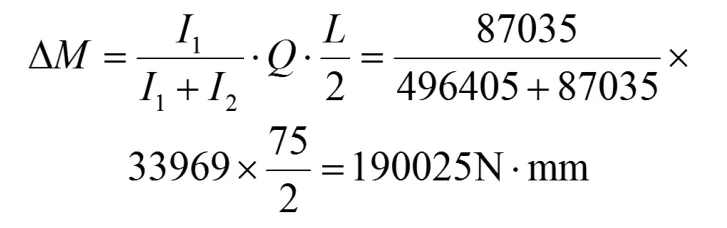
附加弯矩在上缘条产生的附加应力Δσ为:
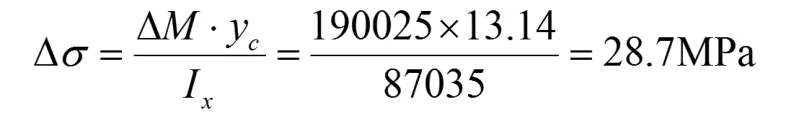
有限元结果,梁上缘条正应力为σ0=-298.4MPa梁上缘条正应力σ=σ0+Δσ=298.4+28.7=327.MPa:已知梁缘条局部失稳临界应力σcr=365MPa
则该段腹板开孔梁上缘条稳定性系数ξ为:

由以上计算过程可知,当开孔向上缘条靠近时,梁上缘条的稳定性系数由ξ=1.01提高到了ξ=1.12,与实际情况不符。开孔附近有较大的应力集中,开孔靠近时,梁缘条的应力应该增加,稳定性系数相应降低。因此按梁缘条的剖面惯性矩的比值来分配腹板剪力,存在局限性。
以下将腹板开孔结构简化为刚框结构,讨论按梁缘条的剖面惯性矩的比值来分配腹板剪力的局限性。并根据参考文献1,将腹板开孔结构简化为板杆结构,推导按开孔上、下部位剩余腹板长度比来分配腹板剪力的理论基础。
2 刚框模型
2.1 理论分析
当梁腹板开口的尺寸接近梁腹板高度时,一般采用环形加强结构如图3所示,L为开口两侧立柱之间距离,H为梁腹板平均高度。腹板的剪切力Q,通过由支柱、梁凸缘、加强环组成的围框的弯曲传递。
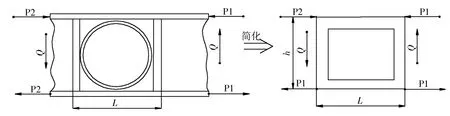
图3 刚框简化示意
由外载荷平衡可知:P
将结构简化为平面刚框(此简化保守),该平面刚框为3度静不定结构。设上缘条抗弯刚度为K1EI,左侧立柱抗弯刚度为K2EI,下缘条抗弯刚度为K3EI,右侧立柱抗弯刚度为K4EI。将刚框上缘条沿开孔圆心处切开,即解除三个多余约束,得静定的基本系统。在切口处用剪力X1、轴力X2、弯矩X3三个未知力代替切口的约束作用,并求出载荷状态《P》和各单位状态《1》、《2》、《3》的内力,如图 4 所示。

图4 刚框的基本系统受力状态
弯矩图画在受压一侧,取刚框外侧为正。
用力法求解该静不定系统,求解过程如下。
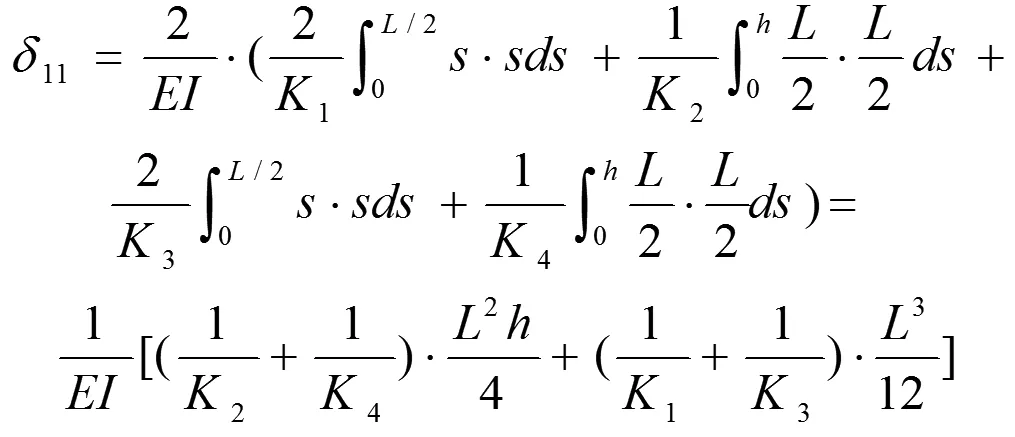
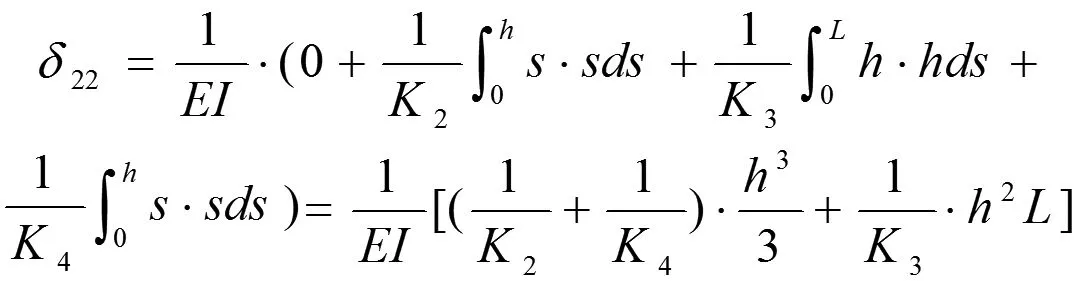
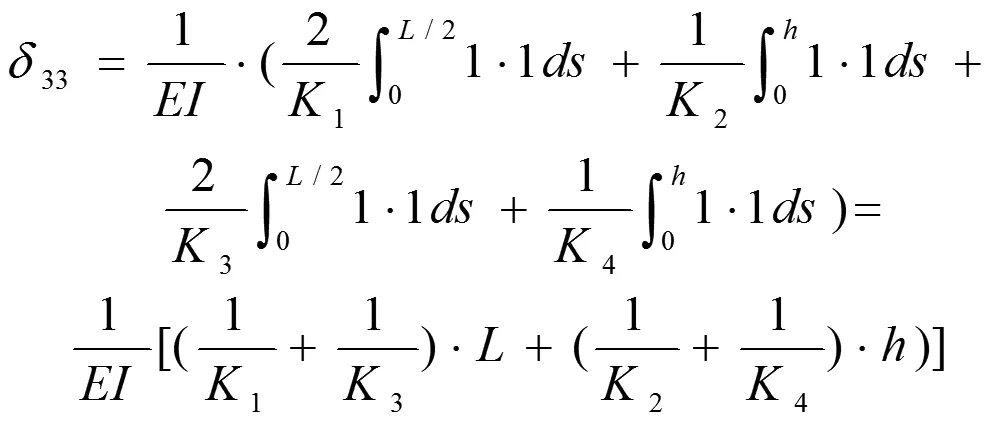
δ12=0 (反对称积分)
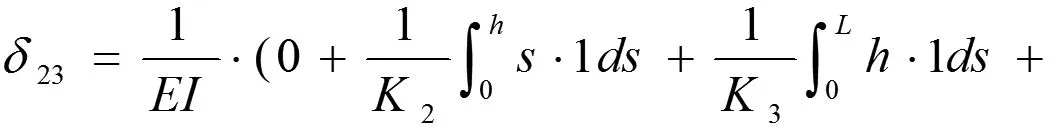
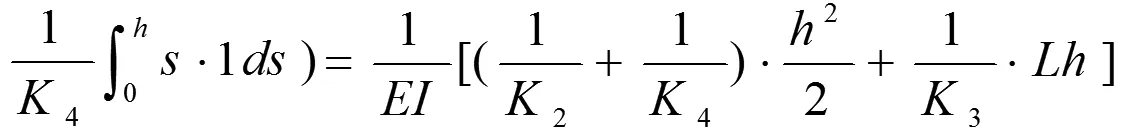
δ13=0 (反对称积分)
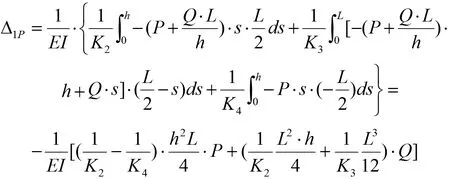


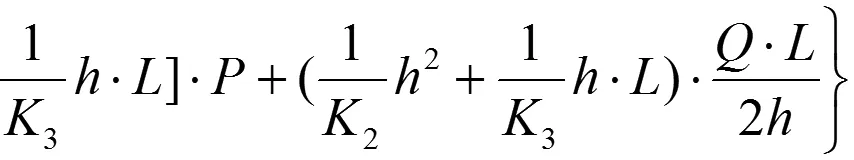
代入典型方程,求解:
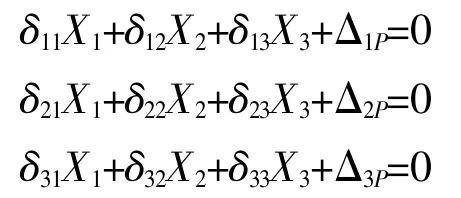
由此可得:
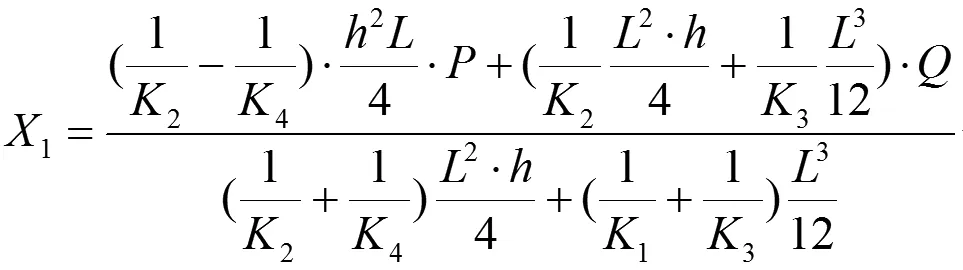

在实际设计中会遇到孔偏离一边的情况,即上缘条抗弯刚度K1EI与下缘条抗弯刚度K3EI不同(K1≠K3)。但是可以认为开孔左、右侧立柱抗弯刚度相同,即左侧立柱抗弯刚度K2EI与右侧立柱抗弯刚度K4EI相同(K2=K4=KV)。则:
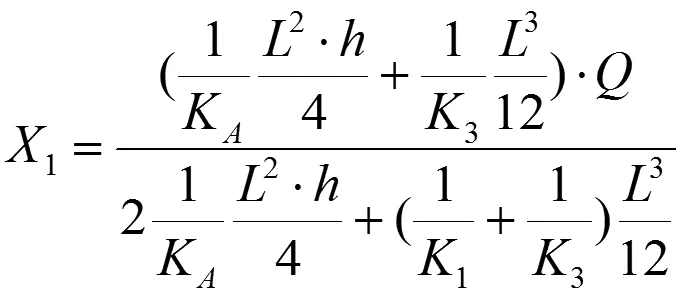
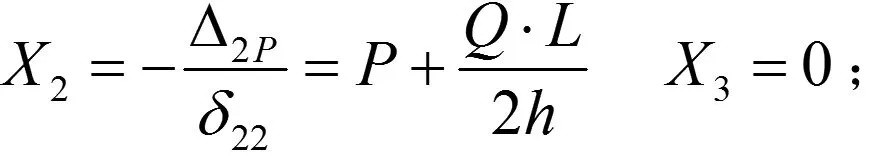
由于梁左右方向(展向)的抗弯刚度远远大于上下方向(高向)的抗弯刚度即,可以假设为无穷小。
此假设偏差ΔX1由下式得:

当K1<K3时 ΔX1>0,此假设冒进。因此,此假设在腹板剩余高度较小的一侧结果冒进,但是此冒进值可能被刚框假设的保守值覆盖。
当K3-K1很大时,存在用刚框假设校核梁腹板开孔强度时结果冒进的情况。
刚框假设:将腹板开孔结构简化为刚框,并认为开孔腹板剩余高度最小处的梁缘剖面惯性矩ISH、IX(上、下梁缘最小的惯性矩)是刚框上、下缘条的剖面惯性矩,即:
一般情况时(开孔不偏心),认为上、下缘条抗弯刚度相同(K1=K2=K3=K4)
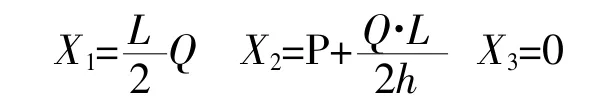
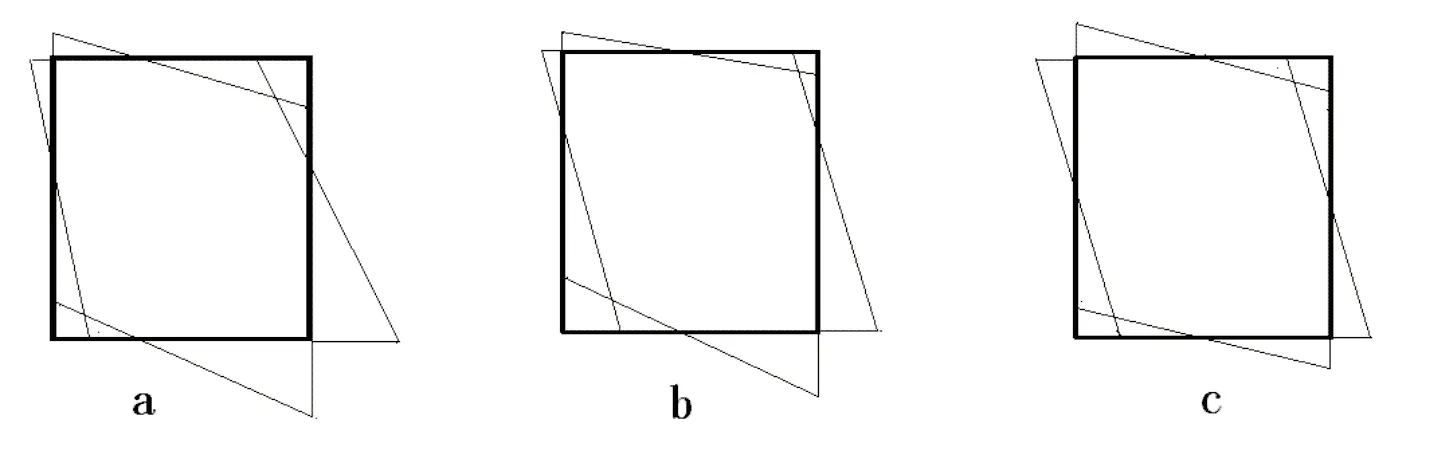
图5 刚框弯矩分布
2.2 实例分析
结构简介:悬臂梁的结构尺寸如图6所示,梁腹板开孔处用环形框加强,材料为铝合金(E=72000MPa,μ=0.3)。该梁一端固定,另一端作用有大小为10000N,方向垂直向上的力。计算结果列于表,曲线图如图7所示。
在此以开孔偏心距离ΔH为唯一变量。开孔直径为L=100mm;梁缘厚度t=5mm,梁缘宽度B=42mm;腹板厚度δ=2mm;环形框宽度B1=100mm,厚度t1=4m。
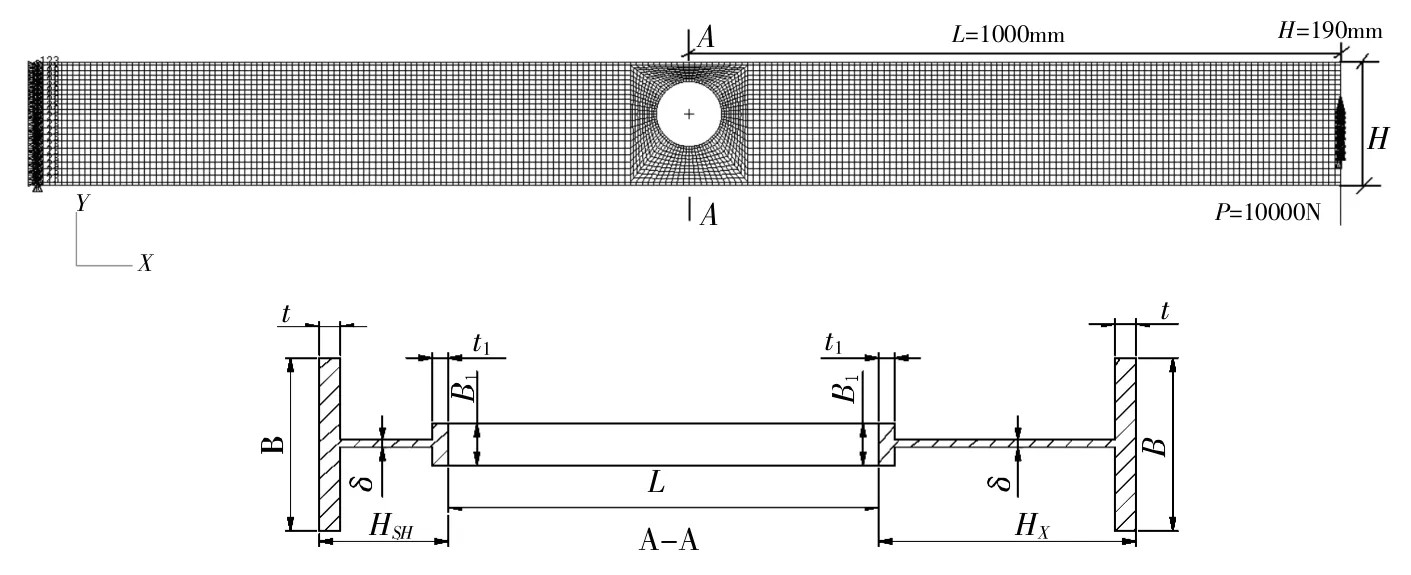
图6 悬臂梁实例
数据分析:表1中是按梁缘条的剖面惯性矩的比值来分配剪力,所得梁上缘条轴应力;是按开孔上、下部位剩余腹板长度比来分配剪力,得到的梁上缘条的轴应力;是有限元细节模型分析所得梁上缘条轴应力。
由表1中数据得,刚框法按开孔截面惯性矩的比值来分配剪力,会出现结果冒进的情况。由上文中对刚框法原理的描述可知,将梁腹板开孔简化为刚框偏保守,而按开孔截面惯性矩的比值来分配剪力偏冒进,一般情况保守值会覆盖冒进值,但是当开孔偏心较大时,按刚框法所计算出的结果会出现偏冒进的情况(图7)。
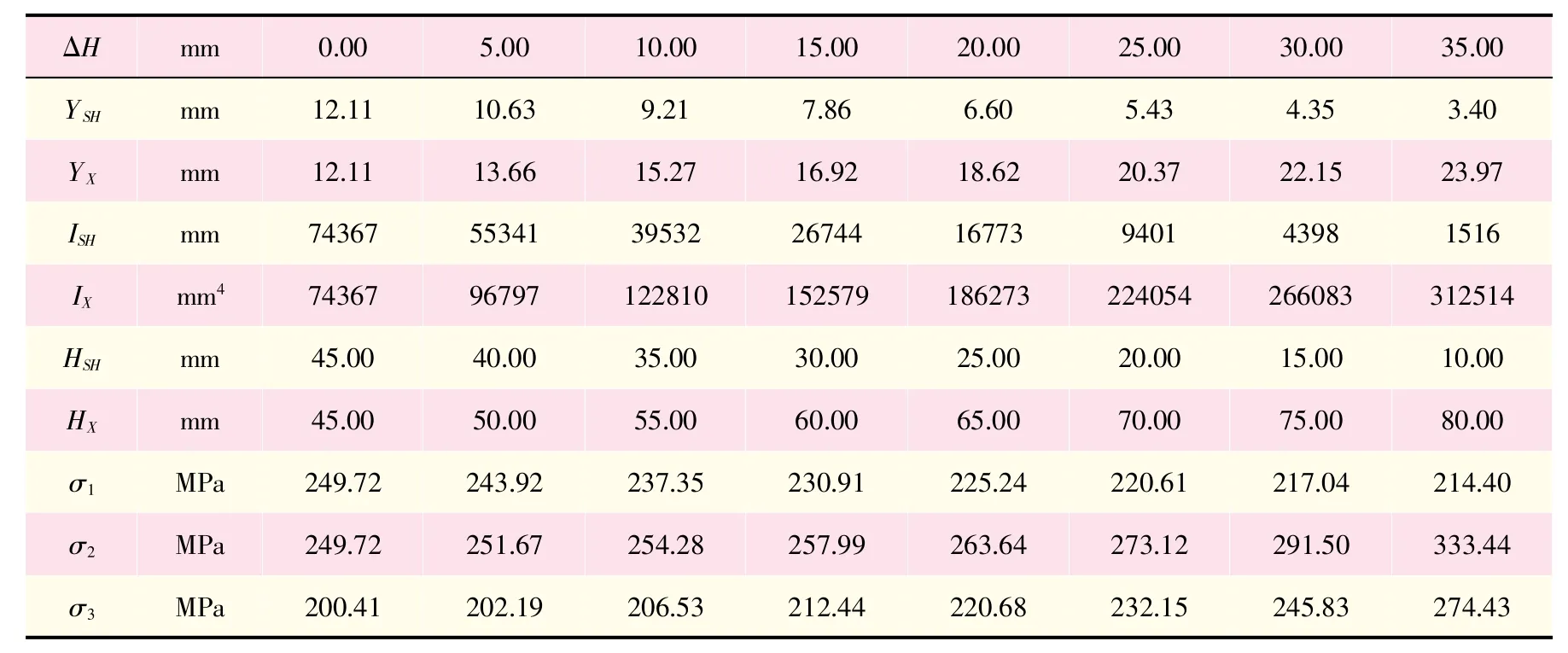
表1 梁腹板开孔偏心情况数据(L=100mm)
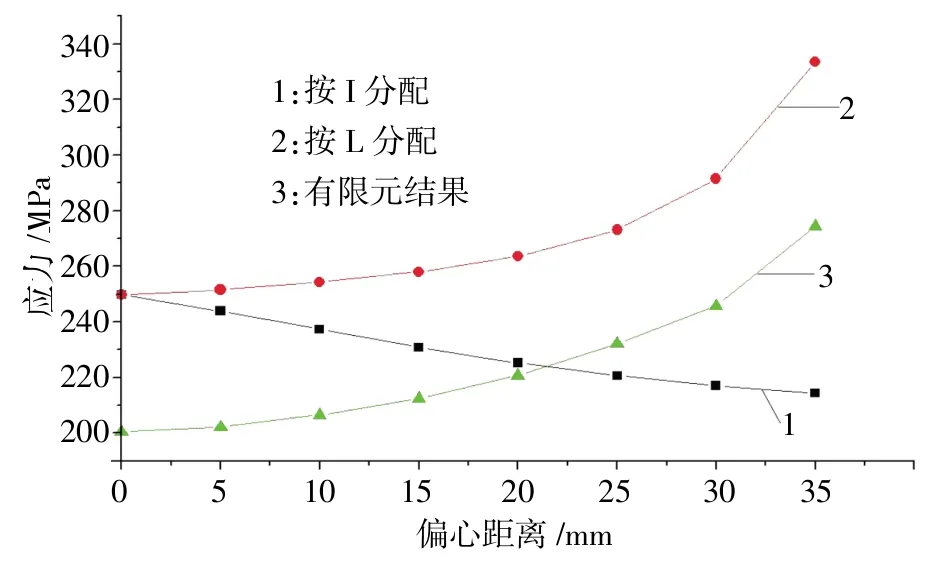
图7 梁腹板开孔偏心情况应力(L=100mm)
3 板杆模型
3.1 理论分析
由前面推导可知,按梁缘条的剖面惯性矩的比值来分配腹板开孔处的剪力,在腹板剩余高度较小的一侧有结果冒进的可能。因此在校核梁腹板开孔强度时,应当按开孔上、下部位剩余腹板高度比来分配剪力。将腹板开孔结构简化为板杆结构,如图8所示,推导按开孔上、下部位剩余腹板长度比来分配剪力的理论基础。其推导过程见参考文献1。
假设开口为覆盖圆孔的方孔如图9所示(此假设保守)。为了便于计算,假设开口区域上方和下方剪流相等,开口左边和右边也相等,即为自身平衡载荷系统。
如果开口不存在,则所有的板剪流q为一个相同的常值。
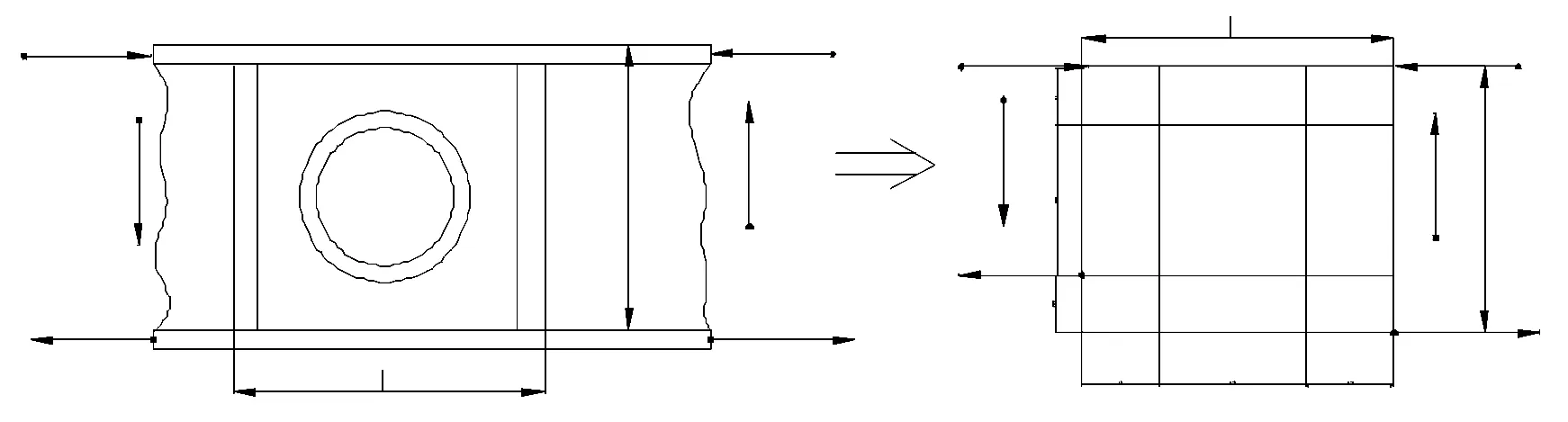
图8 板杆结构简图

图9 按板杆结构简化简图
如果在中间的板上加一个大小相等方向相反的剪流q,中心板上下的剪流则必须与q所引起的力保持静平衡;

将此载荷系统与原来载荷系统相加,得到中间板剪流等于零,即中间板不参与传力,可以等效为中间开孔。此时开孔上下板剪流为:
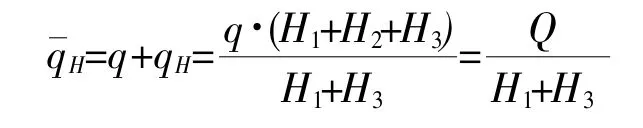
开孔上方板的剪力QH为:
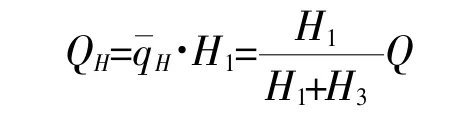
则可计算出中间截面(此处梁缘条的抗弯能力最弱)剪力产生的附加弯矩:
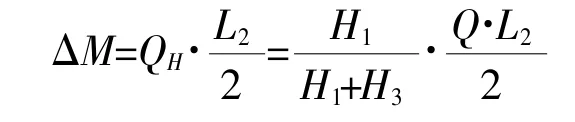
因附加弯矩ΔM的求解过于简单保守,下文将继续讨论如何修正附加弯矩。
一般情况时(开孔不偏心H1=H3),剪流引起的附加弯矩:
3.2 实例分析
结构简介:悬臂的结构尺寸如图10所示,腹板开孔处用环形框加强,材料为铝合金(E=72000MPa,μ=0.3)。该梁一端固定,另一端作用有大小为10000N、方向垂直向上的力。计算结果列于表2。
在此以开孔直径为唯一变量。开孔偏心距离为ΔH=15mm;梁缘厚度t=5mm,梁缘宽度B=42mm;腹板厚度δ=2mm;环形框宽度B1=10mm,厚度t1=4mm。
数据分析:表2中,σ1是按梁缘条剖面惯性矩I的比值来分配剪力所得梁上缘条轴应力;σ2是按开孔上、下部位剩余腹板高度比来分配剪力所得梁上缘条轴应力;σ3是有限元细节模型分析所得梁上缘条轴应力。
由以上推导和计算的结果可知,板杆简化法结果偏保守。
梁腹板开孔编心应力如图11所示,计算结果见表3。
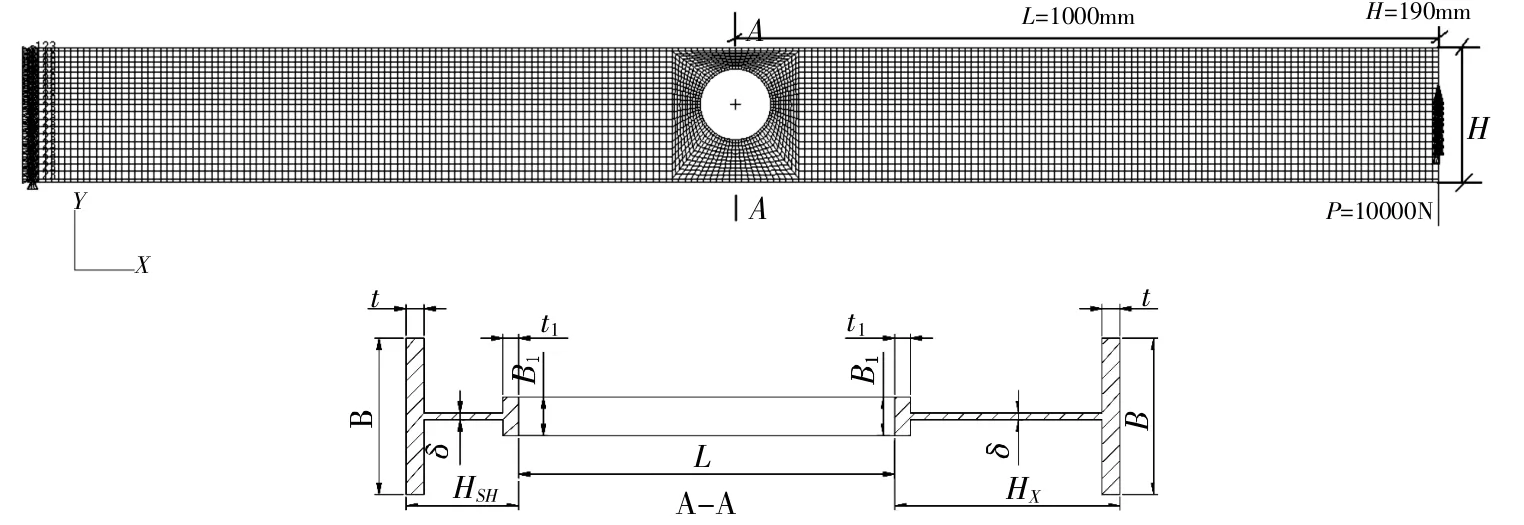
图10 悬臂梁实例简图
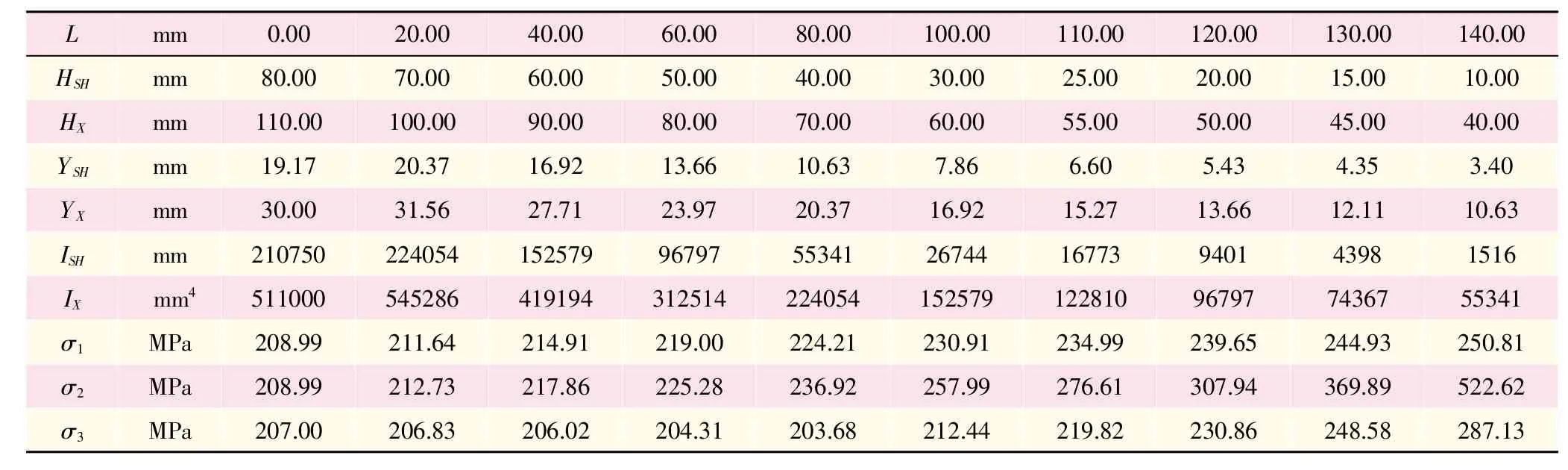
表2 梁腹板开孔偏心情况数据(ΔH=15mm)
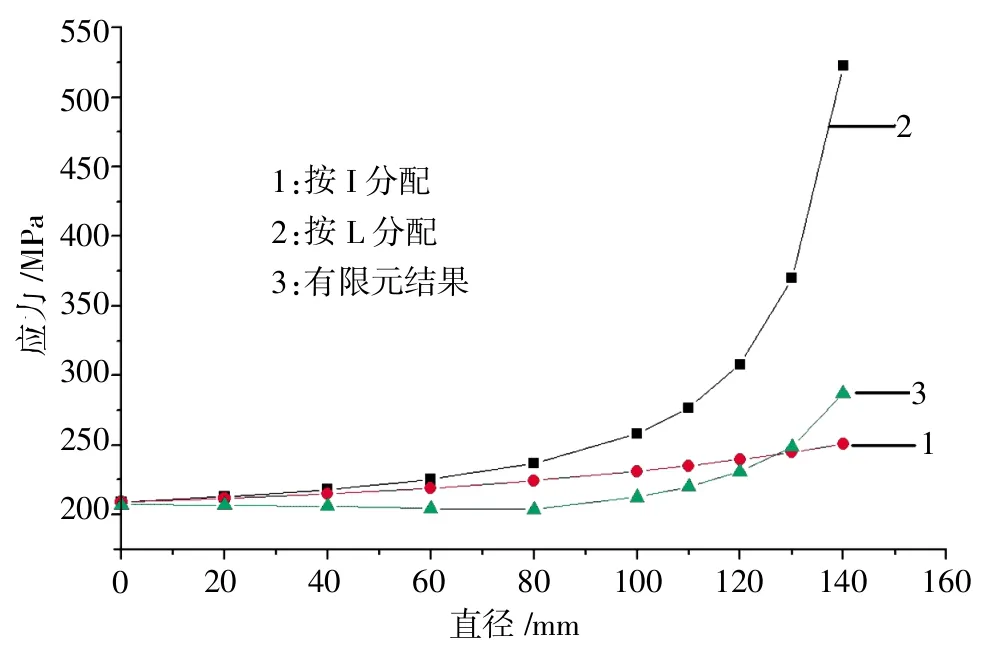
图11 梁腹板开孔偏心情况应力(ΔH=15mm)
以开孔直径为唯一变量。开孔不偏心,既开孔偏心距离为ΔH=0mm;梁缘厚度t=5mm,梁缘宽度B=42mm;腹板厚度δ=2mm;环形框宽度B1=10mm,厚度t1=4mm。计算结果列于表3。

表3 梁腹板开孔居中情况数据
表3中:σ1是按梁缘条的剖面惯性矩I的比值来分配剪力所得梁上缘条轴应力;σ2是按开孔上、下部位剩余腹板高度比来分配剪力所得梁上缘条轴应力;σ3是有限元细节模型分析所得梁上缘条轴应力。
由表3可知,板杆模型法结果过于保守,应该对板杆模型法进行修正。由以上数据可以看出刚框法和板杆法在开孔居中时结果都过于保守,而当开孔偏心时这两种方法的保守值都相对减小。比较刚框法和板杆法可知,这两种方法在处理附加弯矩时方法相同,附加弯矩等于开孔上、下部位剪力传递到开孔中心时引起的弯矩。而处理开孔上、下部位剪力分配时方法不同。经以上实例比较可以认为,刚框法和板杆法处理附加弯矩时均偏保守(开孔居中时无剪力分配问题)。梁腹板开孔居中应力见图12。
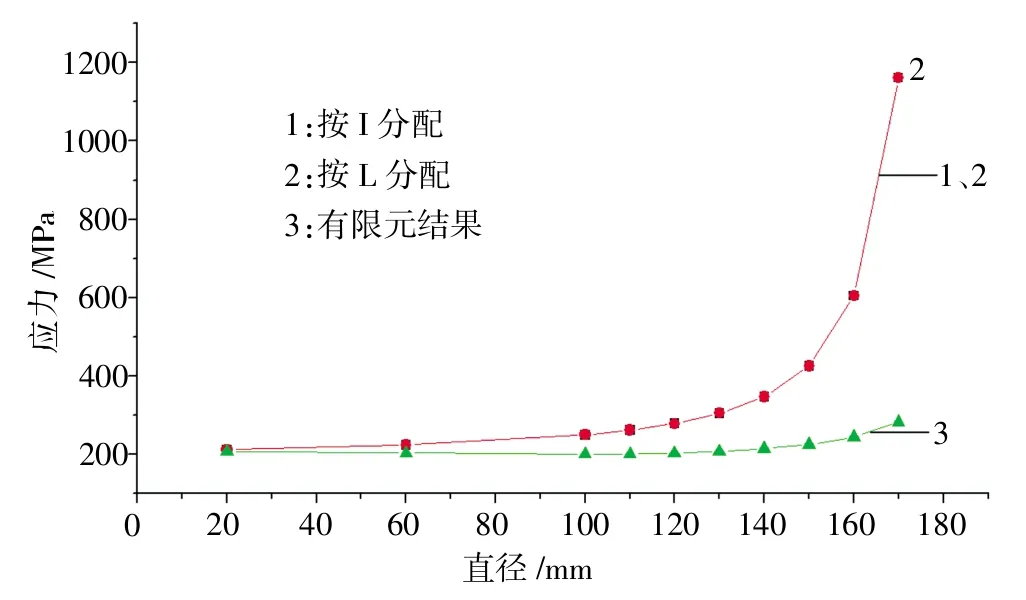
图12 梁腹板开孔居中情况应力
因此,对板杆法过于保守的情况进行修正时,因该主要修正处理附加弯矩时的前提假设,而保留按开孔上、下部位剩余腹板长度比分配总剪力Q的假设。
4 修正附加弯矩
在修正过程中保留按开孔上、下部位剩余腹板长度比分配总剪力Q的假设。
推导过程中认为,附加弯矩等于开孔上、下部位剪力传递到开孔中心时引起的弯矩。在此对附加弯矩进行讨论和修正。
计算中近似认为,剪力QSH、QX传递到开孔上、下部位时产生的弯矩为开孔引起的附加弯矩。该假设过于保守,剪力QSH、QX引起的弯矩既包括开孔引起的附加弯矩,也包括剩余腹板自身剪力产生的弯矩。
可以把开孔部位的剪力分为无开孔时本应该由开孔传递的剪力Q1和上、下腹板传递的剪力Q2,如图13所示。因为开孔无法传递剪力,剪力Q1被传递给附近腹板,导致弯矩增加。因剪力Q1而增加的这部分弯矩是开孔引起的附加弯矩。
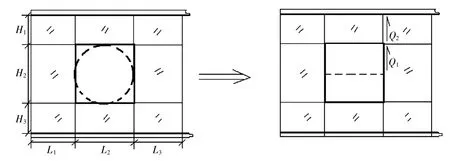
图13 梁腹板开孔载荷分配
假设开孔为方孔。
则上腹板开孔剪力Q1:
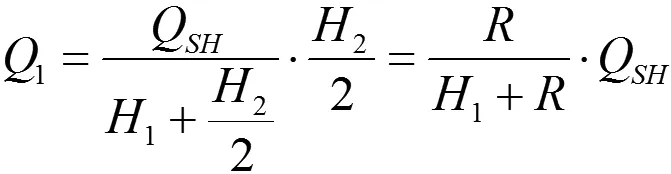
则Q1产生的弯矩ΔH为:
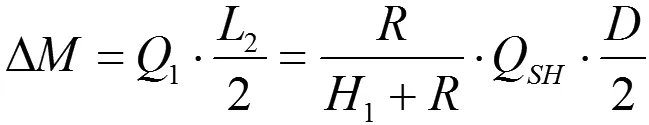
将圆孔假设为方孔偏保守。下面将讨论考虑开孔为圆孔,开孔剪力Q1的求法。
假设腹板没有开孔,将“开孔区域”分为A、B、C三块,如图14所示。A、B区域传递的载荷为Q1=QSH·而B区域的剪力产生的弯矩为附加弯矩。
B区域传递的剪力沿X轴递增,因此B区域传递的剪力可以简化为分布剪力P。
A区域传递的剪力沿X轴递减,因此A区域传递的剪力可以简化为集中剪力Q1加上分布剪力-P。
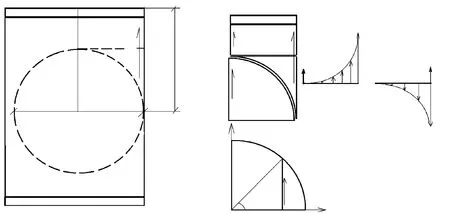
图14 梁腹板开孔载荷分配
已知B区域传递的剪力
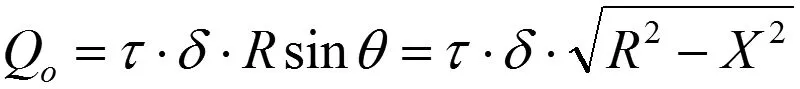
把QO看做一组分布力P,大小为:
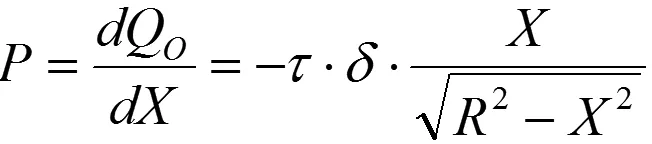
则P产生的弯矩ΔM为:
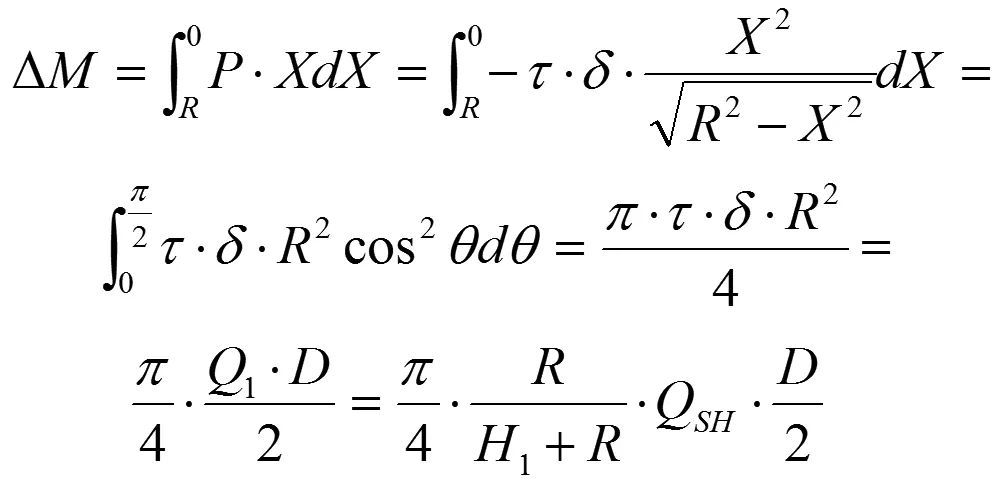
按修正后的附加弯矩公式计算前面的三个实例,结果列于表3开孔直径不变偏心距离改变,曲线如图15所示;表4偏心距离不变开孔直径改变,曲线如图16所示;表5开孔不偏心直径改变,曲线如图17所示,梁腹板开孔居中情况数据见表6。

表4 梁腹板开孔偏心情况数据(L=100mm)
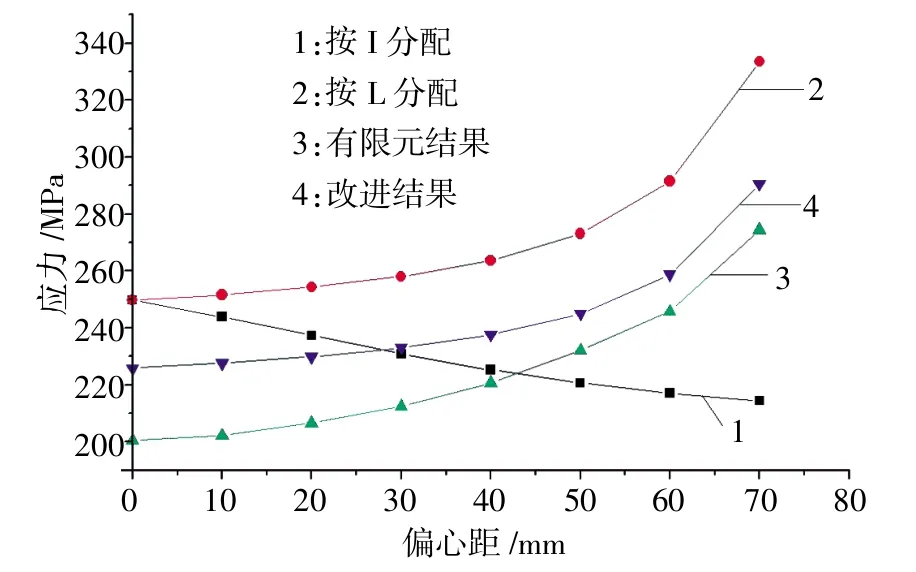
图15 梁腹板开孔偏心情况应力图(L=100mm)
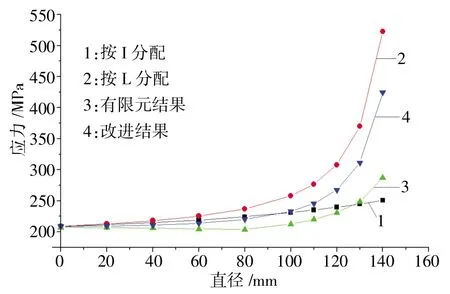
图16 梁腹板开孔偏心情况应力图(△H=15mm)

表5 梁腹板开孔偏心情况数据(△H=15mm)
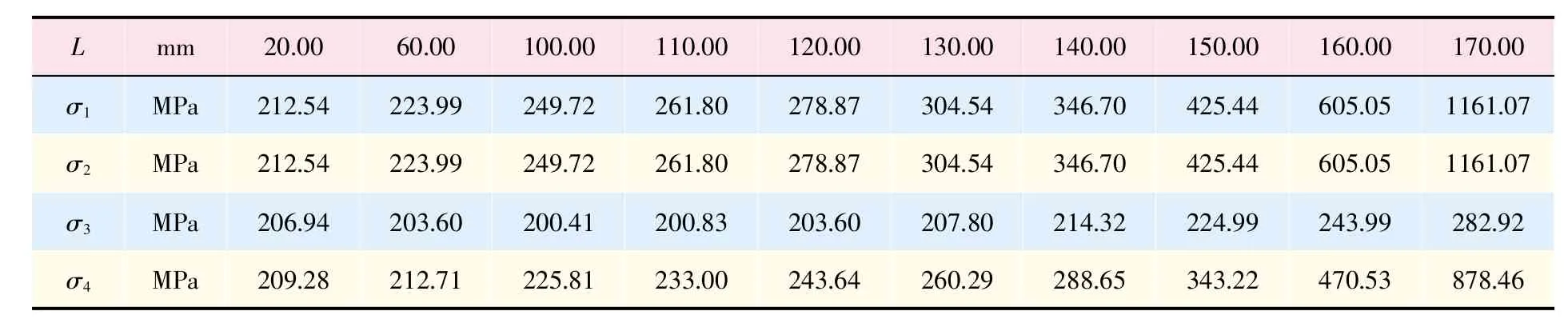
表6 梁腹板开孔居中情况数据
表中:σ1是按梁缘条的剖面惯性矩I的比值来分配剪力所得梁上缘条轴应力;σ2是按开孔上、下部位剩余腹板长度比来分配剪力所得梁上缘条轴应力;σ3是有限元细节模型分析所得梁上缘条轴应力。σ4是修正σ2的附加应力公式所得梁上缘条轴应力。
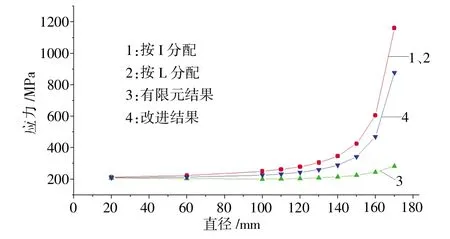
图17 梁腹板开孔居中情况应力
5 结语
按开孔上、下梁缘的剖面惯性矩分配剪力具有局限性。采用该方法处理开孔处剪力分配,在缘条剖面惯性矩较小的一侧结果偏冒进。而将开孔腹板简化为刚框则偏保守,在一般情况下保守值会覆盖冒进值。但是,当开孔偏心较大时,采用该算法所得结果则偏冒进,具有一定风险。因此校核梁腹板开孔时不宜采用该算法。
将翼梁开孔腹板简化为开方孔的板杆结构,开孔处腹板剪力可按开孔上、下腹板剩余高度分配。但求解附加弯矩时,原有方法过于简单保守,由此,本文提出了改进意见。
[1]飞机设计手册编委会.飞机设计手册.第9册.北京:航空工业出版社,2001.
[2]牛春匀.实用飞机结构工程设计.北京:航空工业出版社,2008.
[3]徐芝纶.弹性力学.北京:人民教育出版社,1980.
[4]姜炳光,刘国春.结构力学.北京:国防工业出版社,1983.
[5]庄茁,张帆,岑松.ABAQUS非线性有限元分析与实例.北京:科学出版社,2005.

