针对选址问题的一种遗传算法改进探究*

邹贵祥，张飞舟

(北京大学地球与空间科学学院，北京 100871)

1 引言

选址问题是现代资源配置问题的一个重要分支，涉及城市规划、物流供应、通信建设、应急优化、智能交通等多个方面[1 - 3]。选址问题描述为：在一幅地图中，寻找若干个设址点，所选择的设址点使得以设址点为自变量的整体优化函数达到给定条件下的极值。这里的整体优化函数可以有多种形式，如覆盖内容最大、地图上每个点到设址点的总距离最短、施工消耗最小等。一个好的选址可以在降低建设成本、减少维护支出的同时提高系统工作效率，对生产生活有着重大的意义。随着空间信息智能处理技术的发展，人们发明并组合了越来越多的智能算法来解决选址问题，如遗传算法、蚁群算法、模拟退火算法、微粒群优化算法、人工蜂群算法等[4]。而选址问题是一个多变量的整体优化问题，通用性强、鲁棒性高的遗传算法适合解决这类问题[5]，Zheng等人[6]利用遗传算法为航空材料仓库进行选址，Shao等人[7]使用遗传算法简化计算几何寻找供飞船着陆的最大空白圆的过程，Tang等人[8]使用遗传算法优化支持向量机的参数在高车辆密度城市区域内为车库选址，Khorashad等人[9]使用遗传算法为大学在省级地图上进行了选址。遗传算法利用选择、交叉和变异算子模拟生物种群的进化而达到解决优化问题的目的，但标准遗传算法存在容易陷入早熟的现象，因此人们往往结合问题特征对标准遗传算法进行改进[10]。

选址问题有以下两个特点：地图坐标为自然数；以地图坐标为自变量时，整体优化函数并不连续。本文针对这两个特点，选择二进制编码的遗传算法对选址问题进行求解。二进制的遗传编码方式不仅可以完整地表达地图坐标，定长的编码序列为交叉操作提供方便，非0即1的编码方式极大程度地简化了变异操作[11]。以解决选址过程中遗传算法陷入早熟的问题为目的，本文在探究的基础上，提出了结合小生境技术和多样性测度的遗传算法改进方向。

2 算法概述及改进

2.1 算法概述

标准遗传算法解决选址问题的流程如下：(1)将所选地址的坐标序列按一定规则编码，编码序列形成单个个体。常见的编码方式有二进制编码、实数编码、大字符集编码等[10,11]。(2)以流程(1)中的编码方式重复编码，随机地生成若干个体，这些个体的集合成为初始种群。(3)反解群体中的个体编码，得到群体每个个体的坐标，并计算以个体坐标为自变量时，整体优化函数的值，这个值即为该个体的适应值。(4)根据适应值利用选择算子选出参与交配进化的若干个体，放入交配池。选择算子可以根据具体需求人工设计，一般适应值高的个体被选择概率大。(5)利用交叉算子、变异算子完成交配池中若干个体的交配并产生新一代种群。交叉算子按照一定规律或随机产生交叉点，并将参与交叉的两个个体的交叉点之间的基因序列互换，以此生成新的个体。常见的交叉算子有单点交叉算子、两点交叉算子和多点交叉算子[10]。变异算子则是以一定的概率对新生群体中随机个体的随机位上的基因进行变异，在二进制编码的遗传算法中，变异算子将需要变异的基因位变成该基因位的反。(6)重复选择、交叉和变异的工作，经过标准遗传算法操作的种群将会出现一种表现型，而对应这种表现型的坐标序列则是标准遗传算法对该选址问题的解。

标准遗传算法容易陷入早熟，是因为经过标准遗传算法的选择过程后，种群的多样性逐渐下滑，造成收敛后种群表现型一致的结果[12]。如果收敛的结果并不是全局最优解，那么就称为遗传算法早熟或者收敛至局部最优。解决标准遗传算法陷入早熟的方法有两大类：一类是在一次遗传操作之前，保证种群中适应值大的个体被选择概率大的情况下，对选择算子进行改造或者升级[10,12]；第二类是在一次遗传操作之后引入新的概念或者使用种群的成熟度指标来判断遗传算法是否早熟，从而改进遗传策略[13]。第一类解决方法中，改造升级选择算子的方向之一是自适应地调整选择算子的选择压力[14]。此思想以Boltzmann选择算子、排序选择算子为代表。为了保证合理的动态的选择压力，设计这些选择算子时引入的参数控制变量，可能需要先验的实验数据或者重复的实验才能获得[15,16]。改造升级选择算子的方向之二是调整选择算子的操作方法。此思想以联赛选择、精英选择、稳态选择算子为代表。这些选择算子对于所选入交配池的个体的适应值有相应的要求，设计这些算子时可能不会引入新的变量，相应地，可能会增加种群或者个体之间的比较操作。第二类解决标准遗传算法陷入早熟困境的方法中，可以引入遗传模式的概念，在遗传操作的过程中加入补偿算子[17]、再生算子[18]；可以引入参数衰减因子，自适应地调整交叉概率、变异概率[19,20]；可以根据基因型的构成，使用多点一致交叉算子[21]或者致力于当2个父代染色体相同时也能产生新的子代的基因序列位移的交叉算子[22]；可以引入表明个体间差异的海明距离概念，采用避免相似个体交叉遗传策略[23]；还可以对适应值函数进行线性尺度变换，在前期缩小高适应值个体与低适应值个体的适应值差，后期加大这个差值[23]。不同的种群成熟度指标包括种群个体分布方差、种群的熵、种群个体最佳适应度与平均适应度的差、基因位的多样性[24]、种群的多样度等。其中，群体个体分布方差、种群个体最佳适应度与平均适应度的差均以个体为单位进行计算，反映种群整体的统计状况；种群的熵、基因位的多样性和种群的多样性测度则以每个个体的每位基因为单位进行计算，反映种群的基因分布状况。可以根据每位基因的多样性设计针对每位基因的自适应变异算子[25]，也可以采用部分个体重新初始化的遗传策略[26]。

2.2 使用多样性测度维护

在遗传算法的操作过程中，我们引入一个种群成熟度的观测量——多样性测度，来辅助算法进行遗传策略的选择。

多样性测度的定义如下[10]：

(1)

其中，L为编码长度，n为群体规模大小，群体中的每一个个体以如下形式表示：

aj=(a1j,a2j,…,aLj),j=1,2,…,n

(2)

很明显，多样性测度满足m(A)∈[0,1]，遗传群体的多样性在多样性测度m(A)=1时达到最大，而在多样性测度m(A)=0时消失[10]。对于t代群体，其多样性的测度为m(P(t))，P代表迭代次数为t时的遗传算法种群。对于二进制编码的遗传算法而言，其交叉、变异操作均针对每位基因，多样性测度的计算十分方便。因此，选择多样性测度m来描述选址问题的种群成熟度，当多样性测度下降到一定的值时，再对种群进行相应避免早熟的操作。

相应的遗传策略如下：

(1)每一次选择、交叉、变异操作后，记录进化过程中种群里(包括父代基因池、子代基因池)出现的适应值最高的个体。

(2)完成子代替代父代的操作后，计算种群(指父代基因池)的多样性测度。

(3)当种群的多样性测度降为0时，表明遗传算法收敛了，对比当前种群的最优解个体与记录的适应值最高的个体。

(4)如果当前的最优解个体的适应值低于记录的最高适应值，则重新生成种群(父代基因池)，并把重新生成的父代基因池中的随机选择的一个个体用记录的适应值最高的个体替换，再进行选择、交叉、变异等遗传操作；如果当前种群的最优解个体的适应值等于记录的最高适应值，则视为遗传算法收敛至它所认为的最优解。

(5)由于记录进化过程中种群里出现的适应值最高的个体在计算种群的多样性测度之前，所以此时并不会出现当前种群最优解个体的适应值大于记录的最高适应值的情况。

2.3 预选机制的小生境遗传算法的改进

预选机制的小生境遗传算法会在交叉操作(针对两个父代个体)之后，比较子代个体与产生该子代的父代个体的适应值，当且仅当子代的适应值高于父代时，小生境遗传算法才可以使用子代个体替换父代，完成交叉操作，因而这一“预选机制”能够有效保持群体的多样性[27]，并让种群朝着个体拥有高适应值的方向进化。与预选机制的小生境遗传算法不同：

(1)我们比较完成一次群体地选择交叉变异之后的父、子代群体最优个体的适应值大小来判断进化是否成功。因为选址问题全局优化函数的不连续性，我们不要求每两个父代个体交叉操作后一定产生更优的个体(适应值低的个体有产生适应值高的子代的可能)，但要求子代群体的最优个体适应值不低于父代个体(维持群体的进化进程)。如果新生代的最优个体的适应值比父代的最优个体适应值低，那么就视这次进化“失败”，重新进化。这种操作的最差情况是，基因池并不会被更新(即无论如何选择交叉，无法生成比父代适应值更高的个体)。

(2)若进化成功，将父代和子代的所有个体进行排序，选择适应值高且不重复的若干个体参与下一次进化。对于选址问题而言，遗传算法收敛到一个解，如果这个解不是全局最优解，那么这个解在全局最优解的附近的概率很大。基于预选机制的小生境技术能让这个解跳向一个更优解，然而更优解的方向是不确定的。所以，我们将父子代的全部个体进行排序选择，试图将最优秀的若干个不重复个体保存下来(保证种群的多样性)。

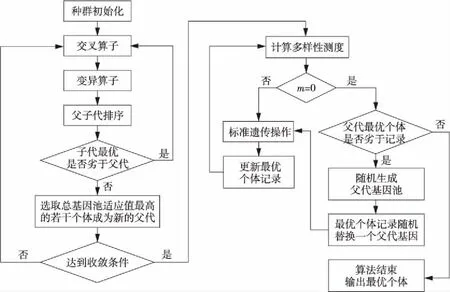
Figure 1 Process of combined algorithm图1 两种算法结合后的算法流程图

(3)设置新的遗传算法收敛条件。小生境遗传算法中，遗传算法的收敛条件是完成若干次进化操作，本文改进的小生境遗传算法的收敛条件则改为：如果进化若干代后，父代基因池最优解并未被替换，则视为改进的小生境遗传算法收敛。父代基因池最优解重复代数越大，算法达到最优解的概率越大，搜索时间也会更长。

2.4 进一步改进的小生境遗传算法

基于2.3节中改进的小生境遗传算法，进一步地，我们取消轮盘赌选择操作，而使父代内的全部个体均参与交叉操作，即每一次选择操作时，选择并未参与交叉操作的两个不同的父代基因序列进行交叉，直至父代基因池中的所有个体均参与了交叉操作。

由交叉操作可知，对所选择的两个个体使用交叉操作有可能产生与被选择个体表现型不同的新个体，这也是遗传算法产生新个体完成搜索的重要操作，但是由公式(1)可知，单纯的交叉操作不会导致种群多样性的减少，选择操作会导致多样性的减少，而多样性的减少是导致遗传算法陷入早熟或者收敛至局部最优解的原因之一。而且，两个基因序列相同的个体进行交叉并不会产生新的个体，轮盘赌选择方法很有可能会选出两个基因序列相同的个体参与交叉操作。我们所期盼的选择、交叉操作的最好结果是：保证种群多样性的同时，又产生适应值更高的个体。因此，我们取消了轮盘赌选择操作，使得父代内的全部个体均参与交叉操作，进一步改进小生境遗传算法。

2.5 改进算法与多样性测度结合

随着遗传算法的进行，基于预选机制小生境算法产生更优解的难度会加大，因此我们将进一步改进的搜索方法安排在求解选址问题的开始阶段，来快速产生较高适应值的解。在进一步改进的小生境遗传算法获得一个适应值较高的认为是“可用解”的时候进入第二个遗传算法操作流程，进行多样性测度维护的遗传计算。在后期使用多样性测度维护的遗传算法有两个好处：其一是利用多样性测度维护的遗传算法中的适应值比例选择方法，可以增加算法的选择压力；其二是使用多样性测度维护的遗传算法能在一定程度上增加遗传算法的“变异概率”。

结合后的算法流程如图1所示。其中，左半部分表示进一步改进的小生境遗传算法，右半部分表示以多样性测度维护的遗传算法。种群初始化后，由于2.4节中取消了选择操作，因此左半部分的遗传算子只包括交叉算子和变异算子，并按2.4节描述使得父代所有个体均参与交叉操作，按照2.3节描述进行排序判断选取适应值较高的若干个体更新基因池后，判断是否达到2.3节中新设置的收敛条件：父代基因池最优解若干代进化都并未被替换。达到收敛条件后进入右半部分的遗传算法流程，其中标准遗传操作包括了轮盘赌选择算子、交叉算子和变异算子，并按照2.2节描述的遗传策略完成遗传算法选址。

3 实验1

3.1 实验参数

地图：10*10的数字地图，地图的每一格都有一个数字。

设址点个数：2～3个。每个设址点的覆盖范围是以设址点为中心的3*3的正方形。

优化目标：2～3个设址点覆盖范围内包含的数字之和最大。覆盖范围有重复的时候，不重复计算。

编码：二进制编码。因为23<10<24，因此表达一个设址点坐标(x,y)的基因二进制序列有8位，表达两个设址点坐标(x1,y1)，(x2,y2)的基因二进制序列有16位，三个设址点对应24位。因为16>10，所以会产生编码冗余。为了使每个坐标被搜索到的概率一致，坐标超过地图范围的编码会被随机指向一个在地图内的坐标。

适应值：一个个体的适应值即是该个体基因表达的设址点覆盖范围内包含的数字之和。数字之和越大，该个体的适应值越高。

群体大小：群体大小设置为20[10]，即每一代的种群都由20个个体(20串16/24位的基因二进制序列)组成。

选择算子：对于标准遗传算法、预选机制的小生境遗传算法、用多样性测度维护的遗传算法和改进的小生境遗传算法，使用适应值比例选择方法中的典型方法：轮盘赌方法。即：对于给定规模为n的群体P={a1,a2,…,an}，个体aj∈P的适应值为f(aj)，其选择概率为：

(3)

对于进一步改进的小生境遗传算法，取消了选择算子。

交叉算子：两点交叉算子。随机生成交叉点p1,p2，用于交叉的两个基因二进制序列的p1位至p2位的基因序列互换。交叉概率设置为0.9[10]。

变异算子：变异概率设置为0.02[10]。以群体中的单个个体为单位，当发生变异时，随机生成变异点pm，该个体的基因二进制序列的pm位基因变为它的反(即1变为0,0变为1)。

算法停止条件：对于标准遗传算法和预选机制的小生境遗传算法，收敛条件设置为进化代数达到上限(1 000代)；对于改进和进一步改进的小生境遗传算法，收敛条件设置为进化代数达到相同上限或者连续10代当前最优解不被更新。

评价方式：以如下三个指标来评价遗传算法的性能：50轮200次实验达到全局最优解次数、在线性能函数与离线性能函数。

在线性能函数的定义如下[10,11,18,28]：

(4)

其中，s为该遗传算法所选择的遗传策略，由编码长度、群体规模大小、交叉概率、变异概率等因子决定。T代表该遗传算法经历过的迭代次数。在线性能函数反映的是遗传群体整体的适应值变化及群体进化能力，它代表着经过平滑处理后的群体平均适应值[10,11,18,28]。

离线性能函数的定义如下[10,11,18,28]：

(5)

其中，s为该遗传算法所选择的遗传策略。

f(a*,t)=max{f(a1,t),f(a2,t),…,f(an,t)}

(6)

指的是迭代次数为t时，t代群体中适应值最高的个体的适应值。离线性能函数反映的是遗传群体中个体的适应值变化以及该遗传算法对更优解的搜索能力，它代表着经过了平滑处理后的群体中适应值最高的个体的平均适应值[10,11,18,28]。

我们随机生成每一次实验的初始种群，同一次实验中五种算法的初始种群相同。

3.2 实验结果及分析

经过实验可以发现，这五种算法都具有达到最优解的能力，但是达到最优解的效果并不相同(如表1所示)，以改进的和进一步改进的小生境遗传算法效果最优。造成差异的原因是，标准遗传算法经过了遗传操作之后，种群的多样性迅速下降，在变异概率不高的情况下，达到早熟或者收敛到局部最优解的概率太大；预选机制的小生境遗传算法进化具有一定“方向性”(向着适应值更高的子代进化)，然而它依旧保留了选择操作，因此效果比标准遗传算法好但劣于其他算法；使用多样性测度来维护的遗传算法在多样性测度达到0时，对比当前最优解和进化过程中所记录的最优解是否一致后，遗传算法收敛到局部最优解(即早熟)的概率下降，然而它的进化不具有“方向性”，因此效果居中；而两种改进的小生境遗传算法进化方向性更强，多样性下降更慢，因此它们收敛到最优解的概率更大；进一步改进的算法取消了选择操作，搜索空间会大于改进的小生境算法，导致它的效果最优。当然，种群大小是导致改进与进一步改进的算法并未达到100%收敛至最优解的原因之一，种群变大，两种改进的遗传算法收敛到全局最优解的概率会变大(如表2所示)。

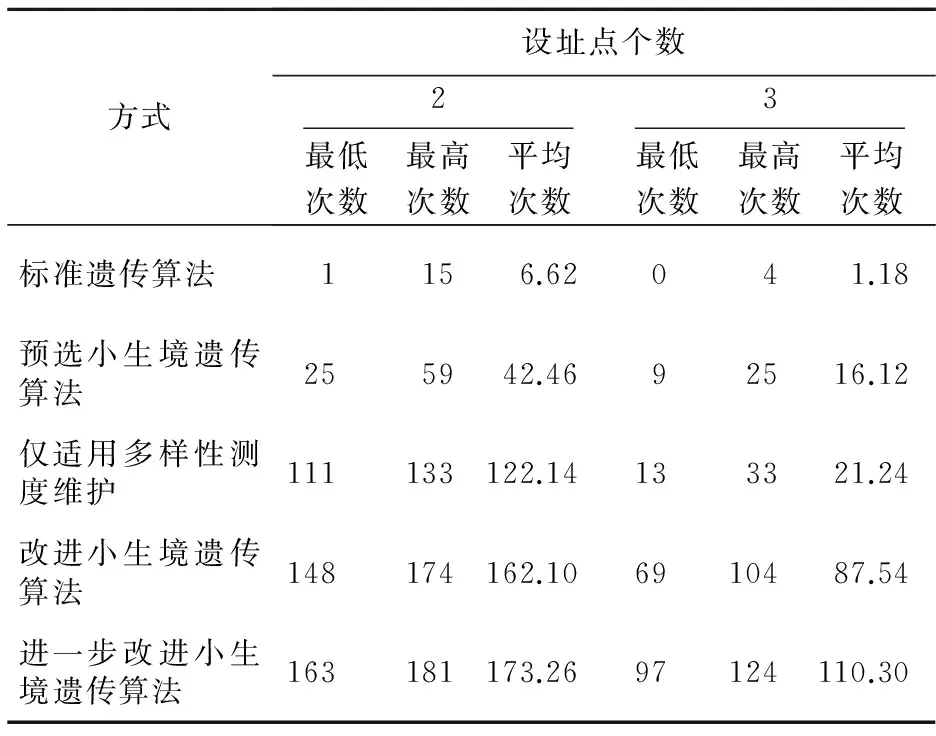
Table 1 Times about algorithms get the max value表1 算法达到最大次数的比较

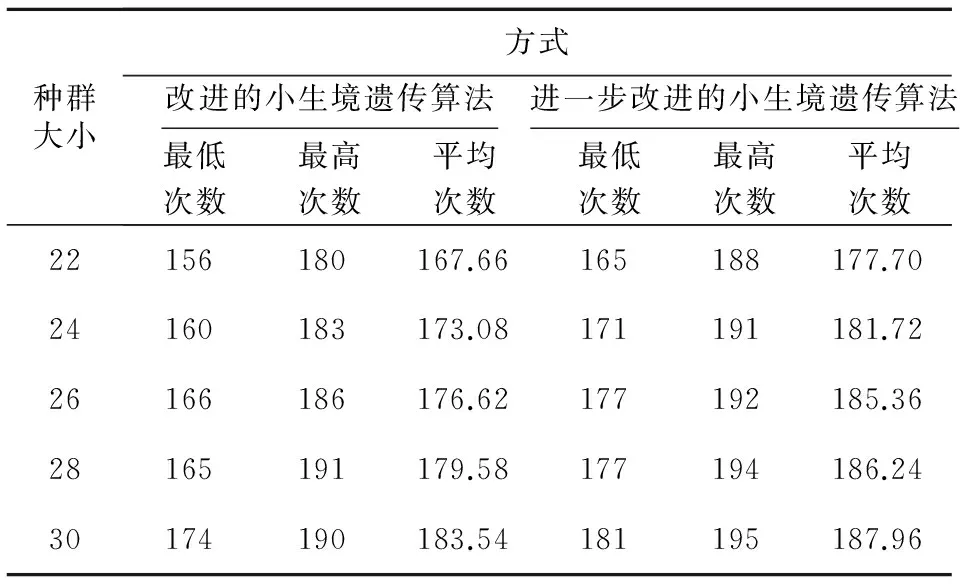
Table 2 Different group population andtimes about algorithms get the max value表2 种群大小与算法性能

从五种算法的随机一次实验的算法性能图(如图2所示)的比较中可以看出，在线性能函数曲线方面，预选机制小生境遗传算法、改进与进一步改进的小生境遗传算法的在线性能函数曲线上升很快，其数值与上升速度均超过了剩下的两种算法，说明这三种算法的种群的平均适应值以及平均适应值的提高速度优于剩下的两种算法，仅使用多样性测度维护的遗传算法在线性能强于标准遗传算法；离线性能函数曲线方面，改进与进一步改进的小生境遗传算法的离线性能函数曲线上升很快，其数值与上升速度均超过了剩下的三种算法，说明改进与进一步改进的小生境遗传算法的最优个体适应值的提高能力和遗传算法的搜索到更优个体的能力优于剩下的三种算法，仅使用多样性测度维护的遗传算法离线性能列第三，其更新种群的方式随机导致算法向最优解收敛的过程随机。从图2中也能看出，虽然这次实验中预选机制小生境遗传算法前100代中种群的平均适应值高，但是最优适应值却不高，说明在这次实验中它已经陷入了早熟的状态。从表1中可以发现，进一步改进的小生境遗传算法达到最优解的次数要高于改进的小生境遗传算法，其原因应该是取消了选择操作而导致算法可以搜索的范围更大，且在图2所示的这次实验中，进一步改进的小生境遗传算法比改进的小生境遗传算法先找到了它认为的最优解，因此它的在线、离线性能函数均高于改进的小生境遗传算法。

Figure 2 Performance comparison of the 5 algorithms图2 五种算法的性能比较曲线图

(记录的)父代基因池最优解连续重复次数是改进与进一步改进的小生境遗传算法中算法收敛条件参数。我们统计了在不同父代基因池最优解连续重复次数下改进的小生境遗传算法的性能。50轮200次10*10数字地图选2个地址的实验结果如表3所示，其中包括200次实验中算法达到最优解(正确解)的最低次数、最高次数和平均次数，每完成200次实验算法的最短用时、最长用时和平均用时。

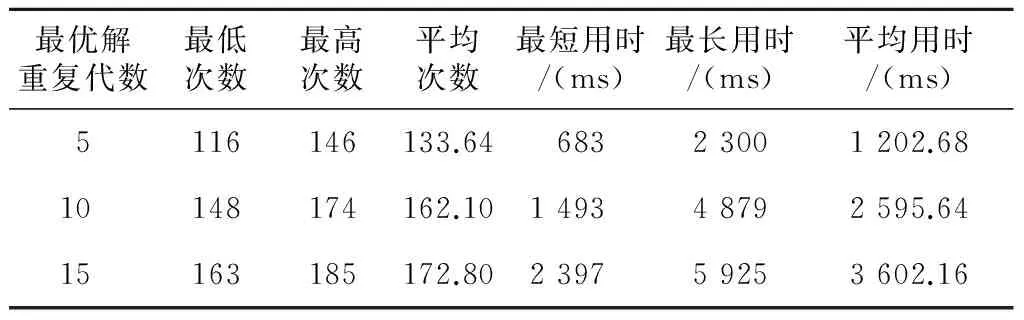
Table 3 Different repetition times of optimum solutionand performance of improved GA with niche technique表3 最优解重复代数与改进的小生境遗传算法性能

考虑到算法准确性和算法用时，我们折衷选择了父代基因池最优解连续重复10次作为改进与进一步改进的小生境遗传算法的收敛条件。

在2.93 GHz英特尔i3处理器4 GB内存32位Windows 7操作系统的实验环境下，小生境遗传算法平均每次迭代用时0.069 ms，改进的小生境遗传算法平均每次迭代用时0.898 ms，进一步改进的小生境遗传算法平均每次迭代用时0.538 ms。算法每迭代一次将更新一次种群，不断迭代完成一次实验。两种改进算法以一定的时间代价换取了更优的种群单次更新效果。

对于改进小生境算法与多样性测度维护结合的实验(流程如图1所示)，从算法性能曲线(如图3所示)中可以看出，第一个流程中使用进一步改进的小生境遗传算法获得一个被认为是“可用解”的过程中，在线性能函数和离线性能函数都快速增长。而之后再进行多样性测度维护后，种群中开始混入适应值较低的个体，形成较大的“变异概率”，所以在线性能函数的值(描述种群平均适应值变化)会降低，之后在线函数的变化由于搜索的随机性而无法预测。在多样性测度达到0之前进行的都是标准遗传操作，当“可用解”适应值很高时，离线性能函数会下降。但是，在多样性测度达到0的时候，因为种群中的最高适应值个体与记录的最优个体相比较和替换(见2.2节)，算法的离线性能函数(描述种群最优个体适应值变化)并不会降低太多。最终我们选取的结果也是维护过程中出现的最优记录个体。

4 实验2

4.1 实验参数

地图：制作70*70的数字地图，包括北至北京市北四环西路，南至阜成路，西至西四环北路，东至西直门北大街的近49 km2的海淀区，涉及到八里庄街道、甘家口街道、曙光街道、紫竹院街道、北下关街道、北太平庄街道、海淀街道、中关村街道、花园路街道等社区。地图的每一格都有一个数字，表示实验区内海淀区各街道社区的人口密度，人口密度数据由2010年第六次人口普查[29]的数据进行计算而得。

设址点个数：模拟设置20个快递点。每个设址点的覆盖范围是以设址点为中心的5*5的正方形。

优化目标：20个设址点覆盖范围内包含的数字之和最大，即覆盖到的人口最多。覆盖范围有重复的时候，不重复计算。

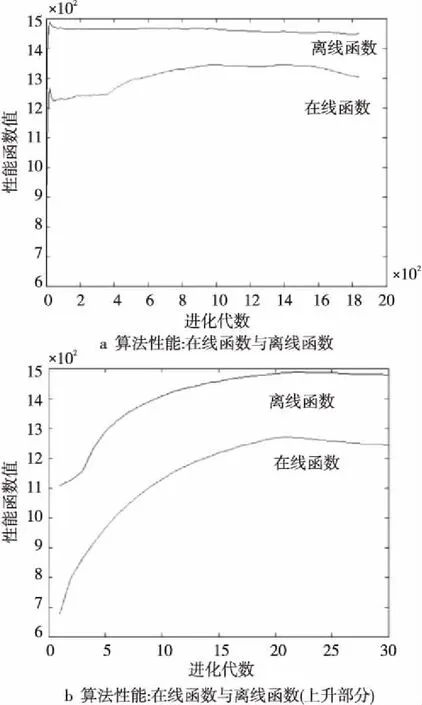
Figure 3 Performance of genetic algorithm combined with 2 algorithms图3 两种算法结合后的遗传算法性能曲线图

算法选择：选择预选机制小生境遗传算法、进一步改进的小生境算法、多样性测度维护与进一步改进的小生境算法结合算法、排挤小生境遗传算法和人工蜂群算法进行实验比较。

排挤小生境遗传算法会随机选择群体中的若干个体，计算群体中的个体与所选个体的相似性，并降低与所选个体相似的个体的适应值，之后参与进化，以保证遗传算法中的群体多样性[30]。

人工蜂群算法同样作为优化算法[4,31 - 34]，它先随机生成若干个蜜源，每个蜜源以20个设址点的坐标表示。使用引领蜂和跟随蜂对蜜源进行优化。与蜜源一一对应的引领蜂在蜜源附近搜索，如果一只引领蜂发现附近的解适应值较高，则更换蜜源。跟随蜂以一定规则选择引领蜂发现的蜜源，并在所选择的蜜源附近进行搜索，如果一只跟随蜂发现附近的解适应值较高，则更换蜜源。记录下引领蜂和跟随蜂发现的适应值最高的蜜源。如此循环两种蜜蜂的操作。如果某只引领蜂所在蜜源若干次循环并未被更换，则放弃当前蜜源，随机生成新的蜜源。人工蜂群算法的重点是由蜜源产生附近蜜源坐标的方法，一般使用的方法是：

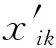
(7)

人工蜂群算法直接以坐标作为蜜源的编码方式，而其余算法与实验1相似，以二进制编码作为编码方式；以覆盖范围内数字总和为适应值函数；以轮盘赌选择方法作为预选机制小生境遗传算法、排挤小生境遗传算法[30]和人工蜂群算法的选择算子；以两点交叉算子作为交叉算子；以单点变异方式为变异算子。对于排挤小生境遗传算法，群体大小设置为30，选取前20个个体遗传到下一代，排挤因子设为3，排挤海明长度设置为0。因为适应值函数的不连续性，并未进行如文献[30]中提到的个体优化，并且全程保持较高的交叉概率以求更大的搜索范围。对于预选机制小生境遗传算法、排挤小生境遗传算法和人工蜂群算法，收敛条件为迭代次数达到迭代上限。对于进一步改进的小生境遗传算法，设置更苛刻的收敛条件为：交叉操作次数与预选机制小生境遗传算法交叉操作次数相等(此时迭代次数一般都未达到迭代上限。在这里，预选机制小生境遗传算法的一次交叉操作指对于种群的一次交叉操作，相当于完成了一次种群的迭代)，或者连续10代当前最优解不被更新。我们进行预选机制小生境遗传算法、进一步改进的小生境遗传算法、两种算法(进一步改进的小生境遗传算法和多样性测度维护)结合的方法、排挤小生境遗传算法和人工蜂群算法对选址问题进行求解。我们随机生成每一次实验的初始种群，同一次实验中五种算法的初始种群相同(排挤小生境算法中有20个个体与剩下的三种遗传算法相同，剩余10个个体随机生成；人工蜂群算法中初始20个蜜源的坐标与其他算法相同)。

4.2 实验结果

我们比较200次实验中，进一步改进的小生境遗传算法的解适应值优于预选机制小生境遗传算法的次数(A)，其优于排挤小生境遗传算法的次数(B)，使用多样性测度维护的进一步改进的小生境遗传算法的解适应值优于进一步改进的小生境遗传算法的次数(C)，其优于排挤小生境遗传算法的次数(D)，和人工蜂群算法的次数(E)。其结果如表4所示。

Table 4 Performance comparison of the 4 algorithms表4 五种算法的结果比较

我们选取使用多样性测度维护的进一步改进算法的随机一次结果，制作了实验所得的快递点选址分布图(如图4所示)。其中，‘+’表示实验选址，‘o’表示由百度地图(搜索关键词为“海淀区顺丰快递”)得出的实验区域内的19个快递点。

Figure 4 Result of site selection图4 选址结果图

4.3 讨论

(1)算法改进方面。

迭代次数相同时，200次实验中，进一步改进的小生境遗传算法均有近70%的概率产生比小生境遗传算法更优的解。说明本文提出的进一步改进的小生境遗传算法是有效的；在多样性测度的维护下，进一步改进的小生境遗传算法也产生过若干次更优解，说明以多样性测度对进一步改进的小生境遗传算法维护的改进遗传算法也是有效的。

随着迭代次数的增加，多样性测度对进一步改进的小生境遗传算法的优化效率降低，这说明随着迭代次数的增加，进一步改进的小生境遗传算法产生的适应值较高的解的效果提升。

迭代次数相同时，进一步改进的小生境遗传算法与排挤小生境遗传算法效果相近，但是增加了多样性测度维护之后，进一步改进的小生境遗传算法比排挤小生境遗传算法效果要好，这说明了多样性测度维护操作的有效性。而两种算法结合的算法性能并未完全优于人工蜂群算法，主要的原因是人工蜂群算法操作的对象是实际坐标，而遗传算法的

变异手段操作的对象是基因序列。在突变概率低的情况下，通过单个基因位变异而达到选址点坐标微小位移的概率太低，而人工蜂群算法却有较大的概率完成坐标微小的位移(公式(7))，这体现出针对基因序列的遗传算法变异操作的局限性。

算法效果的比较也为深入优化遗传算法提供了方向。由于使用多样性维护的遗传算法中采用了适应值比例选择算子担任选择方法，多样性测度为0时新种群的生成方式为随机生成，因此，可以通过改进选择算子、改进新种群生成方式的方法进一步提高多样性测度维护与改进小生境算法结合的遗传算法的计算效率。如可以通过多次实验获得的数据，计算退火温度的初值T，利用Boltzmann选择法自适应地改变选择压力；也可以根据遗传算法的计算进度，在种群多样性测度为0时以所记录的最优个体为中心，以随算法进度改变的不同汉明距离为半径，生成新的种群。一方面可以增大遗传算法达到全局最优解的概率，另一方面，在多样性测度降为0时进行有范围控制的变异操作，以减少新的种群生成的随机性，相比随机生成的新的种群而言更具有“方向性”，因此可以减少算法到达收敛所需要的进化代数，从而提高算法效率。还可以考虑设计针对坐标的变异算子应用于遗传算法的收尾阶段，使得一次变异操作的结果能够限制在变异前坐标的一定范围内。

(2)实验结果方面。

在人口稠密的地区实验选址结果分布得多，而稀薄的地区分布得少。与我们预期的实验结果是相符合的。

(3)与实际情况对比方面。

不巧的是，所选实验区人口密度最大、次大的区域恰巧没有实际的快递点(北太平庄区域)，此区域的快递点位于所选实验区外，这一点并不利于与实际数据的吻合对照。

在实验区人口密度较大的区域，实验所选的快递点与实际存在的快递点有较好的重合。

在实验区人口密度较小的区域，实验所选的快递点与实际存在的快递点重合较差。

进一步分析发现，在实验区人口密度较大的区域，实验所选的快递点分布大致在地铁、高级道路的沿线，而地铁、高级道路往往是街道社区划分的边界线，这个区域的人口密度介于被分开的两个街道社区之间，所以会有较大的人口密度；同时，因为接近地铁、高级道路，方便快递公司与市民取、寄快递，因此快递公司在这些区域设置快递点的概率更大。如中关村街道与北下关街道分界的北三环西路、中关村街道与北太平庄街道、北下关街道与北太平庄街道分界的地铁十三号线沿线上的快递点分布吻合得较好。

再者，快递点选址不只涉及人口因素，还需考虑小区位置、交通、地价等因素，如果加上这些因素对适应值函数进行修改，应该可以产生更吻合实际情况的实验结果。本文的重点在于对选址问题中遗传算法的改进，在算法对照表格中已经可以看到本文算法的改进效果了。

5 结束语

二进制编码的遗传算法可以有效求解优化选址问题。为克服遗传算法在选址过程中陷入早熟的缺点，本文发现使用多样性测度维护的遗传算法可以有效地使遗传算法跳出早熟的结果，同时，针对选址问题的特点，本文改进与进一步改进的小生境遗传算法可以启发式地产生适应值较高的解，并且减少遗传算法达到收敛的代数。因此，本文将进一步改进的小生境遗传算法与使用多样性测度维护的遗传算法相结合，先产生适应值较高的可能解，再以较大变异概率判断是否早熟，使得二者互补，提高遗传算法的计算性能，并通过地图选址实验进行验证，同时指出设计自适应的选择、变异算子和针对坐标的变异算子将会作为我们深入优化遗传算法的方向。

参考文献:

[1] Weng Ke-rui,Xu Zi-hao.Facility location problem with coverings demands limitation[J].Mathematics in Practice and Theory,2014,44(11):191-195.(in Chinese)

[2] Liu Cheng,Chen Ze-hui,Gong Yu-yan.Emergency material storages location problem based on time-satisfaction[J].Mathematics in Practice and Theory,2014,44(17):8-14.(in Chinese)

[3] Wang Ji-guang,Li Jing-feng.Discrete facility location problem in the presence of random disruption[J].Computer Engineering and Applications,2015,51(17):1-7.(in Chinese)

[4] Wang Zhi-gang,Wang Ming-gang,Shang Xu-dong.Solving location problem of distribution centre based on artificial bee colony algorithm[J].Mathematics in Practice and Theory,2014,44(17):170-175.(in Chinese)

[5] Xu Ai-gong,Xu Tao,Zhang Ming-yue,et al.GPS real time point positioning based on genetic algorithm[J].Science of Surveying and Mapping,2009,34(S2):18-20.(in Chinese)

[6] Zheng J,Xu K,Xin Y,et al.The study of selection of air material storehouse based on second generation of genetic algorithm in site[C]∥Proc of International Conference on Information Sciences,Machinery,Materials and Energy,2015:748-751.

[7] Shao W,Cui P,Zhou W.Safe landing site selection based on computational geometry and genetic algorithm[C]∥Proc of International Conference on Natural Computation,2008:660-664.

[8] Tang M,Ren E.Site selection of mechanical parking garage in high density vehicle urban area based on genetic algorithm-support vector machine[C]∥Proc of 2009 2nd International Symposium on Knowledge Acquisition and Modeling,2009:100-102.

[9] Khorashad A K, Kianoosh Z H. Application of genetic algorithm in regional planning (case study:site selection for comprehensive universities)[J].Journal of Basic and Applied Scientific Research,2012,2(11):11428-11433.

[10] Li Min-qiang,Kou Ji-song,Lin Dan,et al.The basic theory and application of genetic algorithm[M].Beijing:Science Press,2002.(in Chinese)

[11] Tian Xin.Study on the hybrid crossover strategy genetic algorithm and its application[D].Baoding:North China Electric Power University,2009.(in Chinese)

[12] Chen Jun-hong.Research on genetic algorithm application in distribution network optimal planning[D].Baoding:Agricultural University of Hebei,2006.(in Chinese)

[13] Wang Min-le,Gao Xiao-guang,Liu Gang.Quantitative analysis and prevention of genetic algorithm premature convergence[J].Systems Engineering and Electronics,2006,28(8):1249-1251.(in Chinese)

[14] Wang Guo-rui.Genetic algorithm with applications in image mosaic[D].Wuhan:Huazhong University of Science and Technology,2006.(in Chinese)

[15] Zhang Yu-hu.The research and implement of classification based on simulated annealing algorithm[D].Qingdao:Qingdao University,2013.(in Chinese)

[16] Wang Xiao-feng, Shang Xu-jing. GA solution of 3-SAT based on clustering ranking selection[J].Journal of Dalian Nationalities University,2009,11(3):267-271.(in Chinese)

[17] Xiong Wei-qing,Wei Ping,Zhao Jie-yu.Research on the premature convergence of genetic algorithms[J].Application Research of Computers,2001,18(9):12-14.(in Chinese)

[18] Lai Zhi-zhu.Long schema genetic algorithms and its applications[D].Chongqing:Chongqing University,2008.(in Chinese)

[19] Xu Yan,Zhi Jing.Optimal PMU configuration based on improved adaptive genetic algorithm[J].Power System Protection and Control,2015,43(2):55-62.(in Chinese)

[20] Aldallal A S.Avoiding premature convergence of genetic algorithm in informational retrieval systems[J].International Journal of Intelligent Systems & Applications in Engineering,2015,2(4):80-85.

[21] Hu Fei-hu,Ma Bei-long,Yang Li,et al.Research on vehicle scheduling optimization in emergency material distribution based on improved genetic algorithm[J].Application Research of Computers,2014,31(10):2928-2932.(in Chinese)

[22] Zhang Qing-hua,Zhang Xi.Application of improved genetic algorithm in vehicle routing problem[J].Journal of Transport Information and Safety,2012,30(5):81-86.(in Chinese)

[23] Jiang J,Meng L D.The strategy of improving convergence of genetic algorithm[J].Telkomnika Indonesian Journal of Electrical Engineering,2012,10(8):2063-2068.

[24] Liu Li,Jing Ping.A mutation strategy dealing with premature convergence of genetic algorithm[J].Electronic Technology & Software Engineering,2015(23):179.(in Chinese)

[25] Liu J,Fu J,Bai X.A new genetic algorithm considering diversity of gene locus[C]∥Prof of the 2nd International Workshop on Materials Engineering and Computer Sciences,2015:764-768.

[26] Nicoară E S. Mechanisms to avoid the premature convergence of genetic algorithms[J].Petroleum-Gas University of Ploiesti Bulletin,Mathematics-I,2009,41(1):87-96.

[27] Zhao Yue,Ru Ting-ting.Comparison and analysis of basic theory and performance on typical genetic algorithms based on niche technique[J].Journal of Tonghua Normal University,2014,35(2):38-39.(in Chinese)

[28] Wang Tong.Research on schema characters in genetic algorithm[D].Zhengzhou:PLA Information Engineering University,2009.(in Chinese)

[29] Census Office of the State Council,Department of population and employment statistics,National Bureau of Statistics.China’s 2010 census information of township,town and street[M].Beijing:China Statistics Press,2012:256-259.(in Chinese)

[30] Hua Jie,Cui Du-wu.Adaptive niche genetic algorithm based on individual optimization[J].Computer Engineering,2010,36(1):194-196.(in Chinese)

[31] He D X,Jia R M.Cloud model-based artificial bee colony algorithm's application in the logistics location problem[C]∥Proc of 2012 International Conference on Information Management,Innovation Management and Industrial Engineering,2012:256-259.

[32] Basti M,Sevkli M.An artificial bee colony algorithm for the p-median facility location problem[J].International Journal of Metaheuristics,2015,4(1):91-113.

[33] Zhang S Z.Optimization of facility location problem in reverse logistics network using artificial bee colony algorithm[C]∥Proc of the 2013 IEEE IEEM,2013:1348-1352.

[34] Yin Jian-xia.Research on artificial bee colony algorithm and its application[D].Xi’an:Xidian University,2012.(in Chinese)

附中文参考文献:

[1] 翁克瑞,许自豪.带覆盖需求约束的设施选址问题[J].数学的实践与认知,2014,44(11):191-195.

[2] 刘诚,陈则辉,龚玉燕.基于时间满意度的应急物资储备库选址问题[J].数学的实践与认知,2014,44(17):8-14.

[3] 王继光,李景峰.随机中断情境下的离散型设施选址问题研究[J].计算机工程与应用,2015,51(17):1-7.

[4] 王志刚,王明刚,尚旭东.基于人工蜂群算法的配送中心选址问题求解[J].数学的实践与认知,2014,44(17):170-175.

[5] 徐爱功,徐涛,张明月,等.GPS动态单点定位的遗传算法探究[J].测绘科学,2009,34(S2):18-20.

[10] 李敏强,寇纪淞,林丹,等.遗传算法的基本理论与应用[M].北京:科学出版社,2002.

[11] 田欣.混合交叉策略遗传算法及其应用研究[D].保定:华北电力大学,2009.

[12] 陈俊红.遗传算法在配电网优化规划中的应用研究[D].保定:河北农业大学,2006.

[13] 汪民乐,高晓光,刘刚.遗传算法早熟问题的定量分析及其预防策略[J].系统工程与电子技术,2006,28(8):1249-1251.

[14] 王国锐.遗传算法及其在图象拼接中的应用[D].武汉:华中科技大学,2006.

[15] 张玉虎.基于模拟退火的分类算法研究与实现[D].青岛:青岛大学,2013.

[16] 王晓峰,尚旭静.基于聚类排序选择方法求解3-SAT问题的遗传算法[J].大连民族学院学报,2009,11(3):267-271.

[17] 熊伟清,魏平,赵杰煜.遗传算法的早熟现象研究[J].计算机应用研究,2001,18(9):12-14.

[18] 赖志柱.长模式遗传算法及其应用[D].重庆:重庆大学,2008.

[19] 徐岩,郅静.基于改进自适应遗传算法的PMU优化配置[J].电力系统保护与控制,2015,43(2):55-62.

[21] 胡飞虎,马贝龙,杨丽,等.基于改进遗传算法的应急物资配送车辆调度优化问题研究[J].计算机应用研究,2014,31(10):2928-2932.

[22] 张华庆,张喜.改进遗传算法在车辆路径问题中的应用[J].

交通信息与安全,2012,30(5):81-86.

[24] 刘丽,景萍.一种抑制遗传算法早熟的变异策略[J].电子技术与软件工程,2015(23):179.

[27] 赵越,茹婷婷.典型小生境遗传算法原理与性能比较分析[J].通化师范学院学报,2014,35(2):38-39.

[28] 汪彤.遗传算法中模式性质研究[D].郑州:解放军信息工程大学,2009.

[29] 国务院人口普查办公室,国家统计局人口和就业统计司.中国2010年人口普查分乡、镇、街道资料[M].北京:中国统计出版社,2012：256-259.

[30] 华洁,崔杜武.基于个体优化的自适应小生境遗传算法[J].计算机工程,2010,36(1):194-196.

[34] 银建霞.人工蜂群算法的研究及其应用[D].西安：西安电子科技大学,2012.